Tải giáo án điện tử dạy thêm Toán 11 KNTT Bài 22: Hai đường thẳng vuông góc
Bài giảng điện tử hay còn gọi là giáo án điện tử powerpoint dạy thêm Toán 11 Kết nối tri thức Bài 22: Hai đường thẳng vuông góc. Bài soạn dạy thêm thiết kế đặc sắc, nhiều hình ảnh, video, trò chơi hấp dẫn. Bộ giáo án có file tải về và chỉnh sửa được. Mời thầy cô tham khảo chi tiết
Rõ nét về file powerpoint trình chiếu. => Xem thêm
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC MÔN TOÁN!
KHỞI ĐỘNG
Thế nào là góc giữa hai đường thẳng m, n trong không gian? Số đo góc giữa hai đường thẳng trong không gian thuộc khoảng giá trị nào?
CHƯƠNG VII: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
BÀI 22: HAI ĐƯỜNG THẲNG VUÔNG GÓC
HỆ THỐNG KIẾN THỨC
- Góc giữa hai đường thẳng
Góc giữa hai đường thẳng m và n trong không gian, kí hiệu (m,n), là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.
Chú ý:
Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b^′ song song với b. Khi đó (a,b)=(a,b^′).
Với hai đường thẳng a,b bất kì: 0^∘≤(a,b)≤90^∘.
- Hai đường thẳng vuông góc
Hai đường thẳng a,b được gọi là vuông góc với nhau, kí hiệu a⊥b, nếu góc giữa chúng bằng 90^∘.
Ví dụ: Hình hộp ABCD.A′B′C′D′ có các mặt là hình vuông.
(AA^′;BC)=90^o;
(AA^′;DC^′)=(DD;DC^′)=45^o
LUYỆN TẬP
PHIẾU BÀI TẬP SỐ 1
DẠNG 1: Tính góc giữa hai đường thẳng
Phương pháp giải:
Tìm góc giữa hai đường thẳng d_1, d_2 bằng cách chọn một điểm O thích hợp (O có thể nằm trên một trong hai đường thẳng).
Từ O dựng các đường thẳng d_1′, d_2′ lần lượt song song với d_1 và d_2. Góc giữa hai đường thẳng d_1, d_2 chính là góc giữa hai đường thẳng d_1′, d_2′ .
Lưu ý: Để tính góc này ta thường sử dụng định lí côsin trong tam giác
Bài 1. Cho tứ diện ABCD có AB=CD=a, IJ=a√3/2 (I, J lần lượt là trung điểm
của BC và AD). Tính số đo góc giữa hai đường thẳng AB và CD.
Giải:
Gọi M, N lần lượt là trung điểm AC, BC
Ta có:
{█(MI=NI=MJ=NJ=1/2AB=1/2CD=a/2@AB // NJ // MI, CD // NI // MJ)┤
⇒ là hình thoi
Gọi O là giao điểm của MN và IJ
Ta có: (MIN) ̂=2(MIO) ̂
Xét ΔMIO vuông tại O, ta có:
cos(MIO) ̂=IO/MI=a√3/4/a/2=√3/2
⇒(MIO) ̂=30°⇒(MIN) ̂=60°
Mà: (AB,CD)=(IM,IN)=(MIN) ̂=60°.
Bài 2. Cho tứ diện ABCD có AB=CD. Gọi I,J,E,F lần lượt là trung điểm của AC,BC,BD,AD. Tính góc (IE, JF)
Giải:
Mặt khác {█(IJ=1/2AB@JE=1/2CD)┤
mà AB=CD nên IJ=JE
Do đó IJEF là hình thoi
Suy ra (IE, JF)=90^0.
Bài 3. Cho hình lập phương ABCD.A_1B_1C_1D_1. Tính số đo giữa hai đường thẳng AC và DA_1.
Giải:
Vì A′C′//AC nên góc giữa AC và DA_1 là (DA_1C_1) ̂.
Vì tam giác DA_1C_1 đều nên (DA_1C_1) ̂=60^0
Vậy góc giữa AC và DA_1 bằng 60^0.
Bài 4. Cho hình lập phương ABCD.EFGH. Hãy tính số đo góc giữa hai đường thẳng AF và EG.
Giải:
Đặt cạnh của hình lập phương trên là a
Gọi I là giao trung điểm EG
Qua A kẻ đường thẳng d//FI
Qua I kẻ đường thẳng d^′//FA
Suy ra d cắt d^′ tại J.
Từ đó suy ra ((EG,AF) ̂)=(EIJ) ̂=α
IJ=AF=2EI=2FI=2AJ=a√2
EJ^2=AE^2+AJ^2=3/2
cosα=|EI^2+IJ^2+AJ^2/2.EI.EJ|=1/2⇒α=60°
Bài 5. Cho tứ diện ABCD đều cạnh bằng a. Gọi M là trung điểm CD, α là góc giữa AC và BM. Tính cosα.
Giải:
Gọi O là trọng tâm của ΔBCD ⇒AO⊥(BCD)
Trên đường thẳng d qua C và song song BM lấy điểm N sao cho BMCN là hình chữ nhật
Từ đó suy ra: ((AC,BM) ̂)=((AC,CN) ̂)=((ACN) ̂)=α
Có:
CN=BM=√3/2a và BN=CN=a/2
AO^2=AB^2−BO^2=AB^2−(2/3BM)^2=2/3a^2
ON^2=BN^2+BO^2=7/12a^2
AN=√AO^2+ON^2=√5/2a
⇒cosα=AC^2+CN^2−AN^2/2AC.CN=√3/6
Bài 6. Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh BC và AD. Cho biết AB=CD=2a và MN=a√3. Tính góc giữa hai đường thẳng AB và CD.
Giải:
{█(OM∥AB@ON∥CD)┤⇒((AB,CD)) ̂=((OM,ON)) ̂
Áp dụng định lí côsin cho tam giác OMN ta có
cos(MON) ̂=OM^2+ON^2−MN^2/2OM.ON=a^2+a^2−(a√3)^2/2.a.a=−1/2
Vậy ((AB,CD)) ̂=60^0.
PHIẾU BÀI TẬP SỐ 2
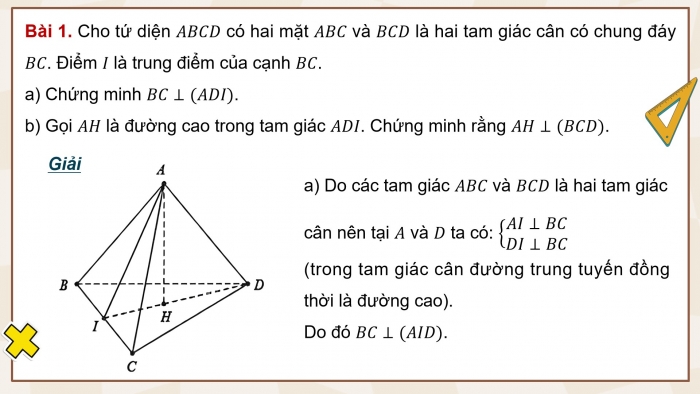
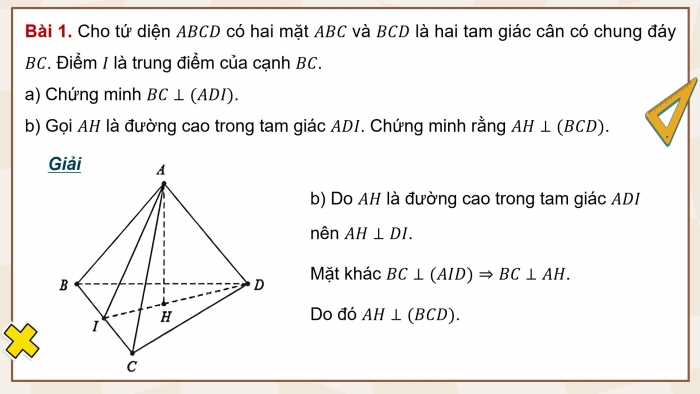
DẠNG 2: Chứng minh hai đường thẳng vuông góc và các bài toán liên quan
...
Hình ảnh về file sile, ppt trình chiếu
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Đang liên tục cập nhật...
Từ khóa tìm kiếm:
Giáo án dạy thêm Powerpoint Toán11 kết nối, Tải giáo án điện tử dạy thêm Toán 11 kết nối tri thức, giáo án powerpoint tăng cường Toán 11 Kết nối Bài 22: Hai đường thẳng vuông góc
