Tải giáo án Powerpoint Toán 10 cánh diều bài 2: Hệ bất phương trình bậc nhất hai ẩn (3 tiết)

CHÀO MỪNG CẢ LỚP ĐẾN VỚI BUỔI HỌC!
Theo Thông báo số 10/2019, giá quảng cáo trên VTV1 là 30 triệu đồng cho 15 giây/1 lần quảng cáo vào khoảng 20h30; là 6 triệu đồng cho 15 giây/1 lần quảng cáo vào khung giờ 16h00 - 17h00.
Một công ty dự định chi không quá 900 triệu đồng để quảng cáo trên VTV1 với yêu cầu quảng cáo về số lần phát như sau: ít nhất 10 lần quảng cáo vào khoảng 20h30 và không quá 50 lần quảng cáo vào khung giờ 16h00 -17h00. Gọi x, y lần lượt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00 -17h00.
Trong toán học, các điều kiện ràng buộc đối với x và y để đáp ứng nhu cầu trên của công ty được thể hiện như thế nào?
Các điều kiện ràng buộc
{█(&x≥10@&0≤y≤50@&30x+6y≤900)┤
BÀI 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN (3 tiết)
I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
HĐ1
Cho hệ bất phương trình: {█(x-y<3 (1)@x+2y> -2 (2))┤
a) Mỗi bất phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?
Mỗi bất phương trình (1) và (2) đều là bất phương trình bậc nhất hai ẩn.
b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên
Giải
Chọn x0=2, y0=1. Khi đó:
(1)⇔2 –1<3⇔1<3 mệnh đề đúng nên (2;1) là nghiệm của bất phương trình (1).
(2)⇔2+2.1>-2⇔4>-2 mệnh đề đúng nên (2;1) là nghiệm của bất phương trình (2).
Vậy cặp số (2;1) là một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.
Kết luận:
Hệ bất phương trình bậc nhất ẩn x, y là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.
Ví dụ 1
Cho hệ bất phương trình sau:
{█(x-2y≤3 (1)@x+y>2 (2) )┤
Cặp số (x;y) nào sau đây là nghiệm của hệ bất phương trình trên?
Giải
+) Thay x=3; y=1 vào hai bất phương trình của hệ, ta có:
3-2.1≤3 là mệnh đề đúng; 3+1>2 là mệnh đề đúng;
Vậy (3;1) là nghiệm chung của (1) và (2) nên (3;1) là nghiệm của hệ bất phương trình.
+) Thay x=1; y=-2 vào bất phương trình (2) của hệ, ta có:
1+(-2)>2 là mệnh đề sai
Vậy (1;-2) không là nghiệm của (2) nên (1;-2) không là nghiệm của hệ bất phương trình.
+) Thay x=5; y=-3 vào bất phương trình (2) của hệ, ta có:
5+(-3)>2 là mệnh đề sai
Vậy (5;-3) không là nghiệm của (2) nên (5;-3) không là nghiệm của hệ bất phương trình.
Luyện tập 1
Chỉ ra một nghiệm của hệ bất phương trình sau
{█(2x+y>0@x-3y<6@x-y ≥ -4)┤
Giải
Thay x=1; y=0 vào 3 bất phương trình của hệ, ta có:
2.1+0=2>0 là mệnh đề đúng;
1-3. 0=1<6 là mệnh đề đúng;
1-0=1≥-4 là mệnh đề đúng.
Vậy (1;0) là nghiệm chung của 3 bất phương trình nên (1;0) là nghiệm của hệ bất phương trình.
II. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Miền nghiệm của hệ bất phương trình là giao các miền nghiệm của các bất phương trình trong hệ.
HĐ2
Cho hệ bất phương trình sau
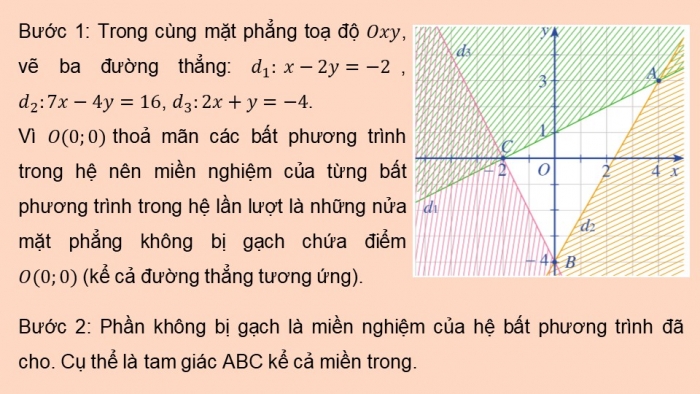
{█(x-2y≥-2@7x-4y≤16@2x+y ≥ -4)┤
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
Bước 1: Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng: d_1: x-2y=-2, d_2:7x-4y=16, d_3:2x+y=-4.
Vì O(0;0) thoả mãn các bất phương trình trong hệ nên miền nghiệm của từng bất phương trình trong hệ lần lượt là những nửa mặt phẳng không bị gạch chứa điểm O(0;0) (kể cả đường thẳng tương ứng).
Bước 2: Phần không bị gạch là miền nghiệm của hệ bất phương trình đã cho. Cụ thể là tam giác ABC kể cả miền trong.
Kết luận: Để biểu diễn miền nghiệm của hệ bất phương trình hai ẩn, ta làm như sau:
+ Trong cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm đó.
+ Phần không bị gạch là miền nghiệm cần tìm.
Ví dụ 2
Biểu diễn miền nghiệm của hệ bất phương trình
{█(&2x+y≤4@&x+y≤3@&x≥0@&y≥0)┤
Giải
Vẽ các đường thẳng: d_1:2x+y=4, d_2:x+y=3, d_3:x=0 và d_4:y=0.
Gạch đi phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là tứ giác OABC kể cả miền trong.
Luyện tập 2
Biểu diễn miền nghiệm của hệ bất phương trình
{█(&3x-y> -3@&-2x+3y<6@&2x+y> -4)┤
Giải
Trên cùng một mặt phẳng tọa độ Oxy, vẽ 3 đường thẳng:
d1:3x –y=-3;
d2:-2x+3y=6;
d3: 2x+y=-4.
Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là phần mặt phẳng không bị gạch sọc không kể đường biên trong hình bên.
III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
Tổng quát, người ta chứng minh được rằng:
Giá trị lớn nhất (hay nhỏ nhất) của biểu thức F(x; y)=ax+by, với (x;y) là tọa độ các điểm thuộc miền đa giác A_1 A_2...A_n, tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.
Bài toán 1
Trong bài toán ở phần mở đầu, tìm x và y sao cho tổng số lần xuất hiện quảng cáo của công ty là nhiều nhất.
Giải
Gọi x,y lần lượt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00-17h00. Theo giả thiết, ta có:
x∈N, y∈N, x≥10, 0≤y≤50.
Tổng số lần phát quảng cáo của công ty là T=x+y
Số tiền công ty cần chi là 30x+6y (triệu đồng)
Do công ty dự định chi không quá 900 triệu đồng nên
30x+6y≤900 hay 5x+y≤150
Ta có hệ bất phương trình:
{█(5x+y≤150@x≥10@0≤y≤50) (I)┤
Miền nghiệm của hệ (I) là miền tứ giác ABCD. Người ta chứng minh được T=x+y đạt GTLN tại cặp số (x;y) là toạ độ một trong các đỉnh của tứ giác ABCD.
Sau khi tính và so sánh giá trị của T tại toạ độ các đỉnh của tứ giác ABCD thì ta được T_max tại x=20, y=50 ứng với toạ độ đỉnh B.
Vậy để phát sóng được số lần quảng cáo nhiều nhất thì số lần phát quảng cáo khoảng 20h30 là 20 lần và vào khung giờ 16h00-17h00 là 50 lần.
Bài toán 2
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và khoảng 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Hỏi phải dung bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Giải
Gọi x,y lần lượt là số tấn nguyên liệu loại I, loại II cần sử dụng.
Khi đó, ta chiết xuất được 20x+10y (kg) chất A và
0,6x+1,5y (kg) chất B.
Theo giả thiết, x và y phải thoả mãn điều kiện:
0≤x≤10, 0≤y≤9; 20x+10y≥140 hay 2x+y≥14;
0,6x+1,5y≥9 hay 2x+5y≥30.
Tổng số tiền cần mua nguyên liệu là: T=4x+3y
Ta có hệ bất phương trình:
{█(0≤x≤10@0≤y≤9@2x+y≥14@2x+5y≥30)┤ (II)
Miền nghiệm của hệ (II) là miền tứ giác ABCD. Người ta chứng minh được T=4x+3y đạt GTNN tại cặp số (x;y) là toạ độ một trong các đỉnh của tứ giác ABCD.
Luyện tập
Bài 1 (SGK-tr.29) Kiểm tra xem mỗi cặp số (x;y) đã cho có phải là nghiệm của hệ bất phương trình đã cho hay không?
a) {█(3x+2y≥-6 @x+4y> 4 )┤(0;2), (1;0)
b) {█(4x+y ≤ -3 @-3x+5y ≥ -12 )┤(-1;-3), (0;-3)
Giải
+) Thay x=0; y=2 vào hai bất phương trình của hệ, ta có:
3. 0+2. 2=4≥-6 là mệnh đề đúng; 0+4. 2=8>4 là mệnh đề đúng.
⟹(0;2) là nghiệm chung của hai bất phương trình.
Vậy (0;2) là nghiệm của hệ bất phương trình trên.
+) Thay x=1; y=0 vào hai bất phương trình của hệ, ta có:
3. 1+2. 0=3≥-6 là mệnh đề đúng;
1+4. 0=1>4 là mệnh đề sai.
⟹(1;0) không là nghiệm chung của hai bất phương trình.
Vậy (1;0) không là nghiệm của hệ bất phương trình.
b) +) Thay x=-1; y=-3 vào hai bất phương trình của hệ, ta có: