Tải giáo án Powerpoint Toán 10 cánh diều bài 6: Ba đường conic

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

                Từ xa xưa, người Hy Lạp đã biết rằng giao tuyến của mặt nón tròn xoay và một mặt phẳng không đi qua đỉnh của mặt nón là đường tròn hoặc đường cong mà ta gọi là đường conic. (Hình 48). Từ “đường conic” xuất phát từ gốc tiếng Hy Lạp konos nghĩa là mặt nón.

Đường conic gồm những loại đường nào và được xác định như thế nào?

BÀI 6:

BA ĐƯỜNG CONIC

NỘI DUNG BÀI HỌC

Đường elip

Đường hypebol

Đường parabol

Một số ứng dụng thực tiễn

của ba đường conic

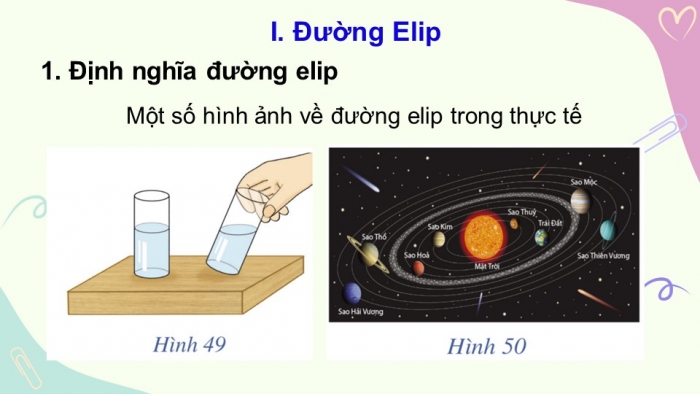
1. Đường Elip
2. Định nghĩa đường elip

Một số hình ảnh về đường elip trong thực tế

Đóng hai chiếc đinh cố định tại hai điểm F₁, F₂ trên mặt một bảng gỗ. Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn 2F₁F₂. Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại vị trí của đầu bút chì (Hình 51). Di chuyển đầu bút chì sao cho dây luôn căng, đầu bút chì vạch nên một đường mà ta gọi là đường elip. Gọi vị trí của đầu bút chì là điểm M.

Khi M thay đổi, có nhận xét gì về tổng MF₁ + MF₂?

Giải

Ta thấy tổng MF₁ + MF₂ luôn bằng độ dài vòng dây kín, do đó khi M thay đổi, tổng MF₁ + MF₂ là
 một độ dài không đổi.

KẾT LUẬN
Cho hai điểm F₁, F₂ cố định có khoảng cách

F₁F₂ = 2c (c > 0).

Đường elip (còn gọi là elip) là tập hợp các điểm M trong mặt phẳng sao cho MF₁ + MF₂ = 2a, trong đó a là số cho trước lớn hơn c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của elip.

2. Phương trình chính tắc của elip

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF₁ + MF₂ = 2a, ở đó F₁F₂ = 2c (với a > c > 0).

Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F₁F­₂, trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 52). Khi đó, F₁(– c; 0) và F₂(c; 0) là hai tiêu điểm của elip (E). Chứng minh rằng:

1. a) A₁(– a; 0) và A_2­(a; 0) đều là giao điểm của elip (E) với trục Ox.
2. b) B₁(0; – b) và B₂(0; b), ở đó , đều là giao điểm của elip (E) với trục Oy.

Giải

1. Do A₁F₁ = a – c và A₁F₂ = a + c nên A₁F₁ + A₁F₂ = 2a.

Vậy A₁(-a; 0) thuộc elip (E).

Mà A₁ (-a; 0) thuộc trục Ox nên A₁(-a; 0) là giao điểm của elip (E) với trục Ox.

Tương tự, ta chứng minh được A₂(a; 0) là giao điểm của elip (E) với trục Ox.

1. Ta có:

B₂F₂ =

Vì B₂F₁ = B₂F₂ nên B₂F₁ + B₂F₂ = a + a = 2a.

Do đó, B₂(0; b) thuộc elip (E). Mà B₂(0; b) thuộc trục Oy nên B₂(0; b) là giao điểm của elip (E) với trục Oy.

Tương tự, ta chứng minh được: B₁(0; -b) là giao điểm của elip (E) với trục Oy.

Như vậy, elip (E) đi qua bốn điểm A₁(-a; 0), A₂(a; 0), B₁(0; -b), B₂(0; b), với b =

KẾT LUẬN

Khi chọn hệ trục toạ độ như trên, phương trình đường elip có thể viết dưới dạng:

Trong đó, a > b > 0

Đây gọi là phương trình chính tắc của elip.