Giải chuyên đề học tập Toán 10 Cánh diều bài 1: Phương pháp quy nạp toán học

Khởi động

Câu hỏi: Chia hình vuông cạnh 1 thành bốn hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{2}$.

Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{4}$

Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở Hình 1.

Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?

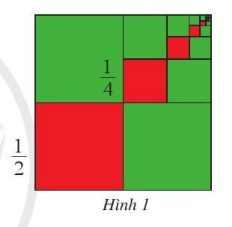
Hướng dẫn trả lời:

Ta có: Hình vuông nhỏ thứ nhất có cạnh bằng $\frac{1}{2}$

Hình vuông nhỏ thứ hai có cạnh bằng nửa hình vuông nhỏ thứ nhất và bằng $\frac{1}{4}=\frac{1}{2^{2}}$

Hình vuông nhỏ thứ ba sẽ có cạnh bằng nửa hình vuông nhỏ thứ hai và bằng $\frac{1}{2}\times\frac{1}{4}=\frac{1}{8}=\frac{1}{2^{3}}$

Tiếp tục như thế hình vuông nhỏ thứ n sẽ có cạnh bằng $\frac{1}{2^{n}}$

I. Phương pháp quy nạp toán học

Hoạt động: Xét mệnh đề chứa biến P(n) : "1 + 3 + 5 + ... + (2n – 1) = n$^{2}$" với n là số nguyên dương.

a) Chứng tỏ rằng P(1) là mệnh đề đúng.

b) Với k là một số nguyên dương tuỳ ý mà P(k) là mệnh đề đúng, cho biết 1 + 3 + 5 + ... + (2k – 1) bằng bao nhiêu.

c) Với k là một số nguyên dương tuỳ ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra $k^{2} + [2(k + 1) – 1] = (k+1)^{2}$.

Hướng dẫn trả lời:

a) Ta có P(1): "1 = 1$^{2}$". Mệnh đề này đúng vì $1^{2}$ = 1.

b) Với k là một số nguyên dương tuỳ ý mà P(k) là mệnh đề đúng thì 1 + 3 + 5 + ... + (2k – 1) = k$^{2}$.

c) Khi P(k) là mệnh đề đúng. Ta có:

P(k+1) = 1 + 3 + 5 + ... + (2k – 1) + [2(k+1) – 1] = P(k) + [2(k+1) – 1]

=$ k^{2} + [2(k+1) – 1] = k^{2} + (2k + 2 – 1) = k^{2} + 2k + 1 = (k+1)^{2}$

Vậy P(k+1) cũng là mệnh đề đúng.

Luyện tập 1. Chứng minh rằng với mọi n ∈ ℕ* ta có

$a) \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-1$

$b)\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{n^{3}-1}{n^{3}+1}=\frac{2(n^{2}+n+1}{3n(n+1)}$

Hướng dẫn trả lời:

a)

• Khi n = 1, ta có:

$\frac{1}{\sqrt{1}+\sqrt{2}}=\frac{\sqrt{2}-1}{(\sqrt{1}+\sqrt{2})(\sqrt{2}-1)}=\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-1^{2}}=\frac{\sqrt{2}-1}{1}=\sqrt{2}-1=\sqrt{1+1}-1$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là:

$\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}=\sqrt{(k+1)+1}-1$

Thật vậy, theo giả thiết quy nạp ta có:

$\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{k}+\sqrt{k+1}}=\sqrt{k+1}-1$

Khi đó:

$\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}$

$=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{k}+\sqrt{k+1}}+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}$

$=(\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{k}+\sqrt{k+1}})+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}$

$=(\sqrt{k+1}-1)+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}$

$=(\sqrt{k+1}-1)+\frac{1}{\sqrt{k+1}+\sqrt{(k+1)+1}}$

$=(\sqrt{k+1}-1)+\frac{\sqrt{(k+1)}+1-\sqrt{k+1}}{(\sqrt{k+1}+\sqrt{(k+1)+1})(\sqrt{(k+1)+1}-\sqrt{k+1}}$

$=\sqrt{\sqrt{k+1}-1}+\frac{\sqrt{(k+1)+1}-\sqrt{k+1}}{[(k+1)+1]-(k+1)}$

$=(\sqrt{k+1}-1)+(\sqrt{9k+1)+1}-\sqrt{k+1})$

$=\sqrt{(k+1)+1}-1$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈  ℕ*.

b)

• Khi n = 2, ta có: $\frac{2^{3}-1}{2^{3}+1}=\frac{7}{9}=\frac{2(2^{2}+2+1)}{3 2(2+1)}$

Vậy mệnh đề đúng với n = 2.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là:

$\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{(k+1)^{3}-1}{(k+1)^{3}+1}=\frac{2[(k+1)^{2}+(k+1)+1}{3(k+1)[(k+1)+1]}$

Thật vậy, theo giả thiết quy nạp ta có:

$\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{k^{3}-1}{k^{3}+1}=\frac{2(k^{2}+k+1)}{3k(k+1)}$

Khi đó:

$\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{(k+1)^{3}-1}{(k+1)^{3}+1}$

$=\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{k^{3}-1}{k^{3}+1}\times\frac{(k+1)^{3}-1}{(k+1)^{3}+1}$

$=(\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{k^{3}-1}{k^{3}+1})\times\frac{(k+1)^{3}-1}{(k+1)^{3}+1}$

$=\frac{2(k^{2}+k+1)}{3k(k+1)}\times\frac{(k+1)^{3}-1}{(k+1)^{3}+1}$

$=\frac{2(k^{2}+k+1)}{3k(k+1)}\times\frac{[(k+1)-1][(k+1)^{2}+(k+1)+1}{[(k+1)^{2}-(k+1)+1]}$

$=\frac{2(k^{2}+k+1)}{3k(k+1)}\times\frac{k[(k+1)^{2}+(k+1)+1}{[(k+1)+1](k^{2}+k+1)}$

$=\frac{2}{3(k+1)}\times\frac{[(k+1)^{2}+(k+1)+1]}{[(k+1)+1]}$

$=\frac{2[(k+1)^{2}+(k+1)+1]}{3(k+1)[(k+1)+1]}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

II. Áp dụng

Luyện tập 2. Chứng minh với mọi n ∈ ℕ*, $(1+\sqrt{2})^{n},(1-\sqrt{2})^{n}$ lần lượt viết được ở dạng $a_{n}+b_{n}\sqrt{2}, a_{n}-b_{n}\sqrt{2}$ , trong đó an, bn là các số nguyên dương.

Hướng dẫn trả lời:

• Khi n = 1, ta có:

$(1+\sqrt{2})^{1}=1+\sqrt{2}=1+1 \times \sqrt{2}\Rightarrow a_{1}=1,b_{1}=1$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $(1+\sqrt{2})^{k+1}$ viết được dưới dạng $a_{k+1}+b_{k+1}\sqrt{2}$  trong đó $a_{k+1},b_{k+1}$  là các số nguyên dương.

Thật vậy, theo giả thiết quy nạp ta có: $(1+\sqrt{2})^{k}=a_{k}+b_{k}\sqrt{2}$ với $a_{k},b_{k}$ là các số nguyên dương.

Khi đó:

$(1+\sqrt{2})^{k+1}=(1+\sqrt{2})^{k}(1+\sqrt{2})=(a_{k}+b_{k}\sqrt{2})(1+\sqrt{2})$

$=a_{k}\times 1+b_{k}\sqrt{2} \times 1+a_{k}\times \sqrt{2}+b_{k}\sqrt{2}\times \sqrt{2}=a_{k}+b_{k}\sqrt{2}+a_{k}\sqrt{2}+2b_{k}$

$=(a_{k}+2b_{k})+(a_{k}+b_{k})\sqrt{2}$

Vì $a_{k},b_{k}$ là các số nguyên dương nên $a_{k}+2b_{k}$ và $a_{k}+b_{k}$  cũng là các số nguyên dương.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

• Theo chứng minh trên ta có:

Với mọi n ∈ ℕ* thì  $(1\sqrt{2})^{n}=a_{n}-b_{n}\sqrt{2}$ với $a_{n}, b_{n}$ là các số nguyên dương.

Chứng minh tương tự ta được:

Với mọi n ∈ ℕ* thì $(1-\sqrt{2})^{n}=c_{n}-d_{n}\sqrt{2}$ với $c_{n},d_{n}$ là các số nguyên dương.

Giờ ta chứng minh $a_{n}=c_{n}$ và $b_{n}= d_{n}$ với mọi n  ℕ*.

Xét mệnh đề P(n):  và  với mọi n ∈ ℕ*.

• Khi n = 1, ta có:

$(1+\sqrt{2})^{1}=1+\sqrt{2}=1+1 \times \sqrt{2}\Rightarrow a_{1}=1,b_{1}=1$

$(1-\sqrt{2})^{1}=1-\sqrt{2}=1-1 \times \sqrt{2}\Rightarrow c_{1},d_{1}=1$

Vậy $a_{1}=c_{1},b_{1}=d_{1}$

Vậy mệnh đề P(n) đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề P(n) cũng đúng với k + 1, tức là: $a_{k+1}=c_{k+1}$ và $b_{k+1}=d_{k+1}$

Thật vậy, theo giả thiết quy nạp ta có: $a_{k}=c_{k}$ và $b_{k}=d_{k}$ (1).

Mặt khác:

$(1+\sqrt{2})^{k+1}=(1+\sqrt{2})^{k}(1+\sqrt{2})$

$=(a_{k}+b_{k}\sqrt{2})(1+\sqrt{2})=a_{k}\times 1+b_{k}\sqrt{2}+a_{k}\times \sqrt{2}+b_{k}\sqrt{2}\times \sqrt{2}$

$=a_{k}+b_{k}\sqrt{2}+a_{k}\sqrt{2}+2b_{k}=(a_{k}+b_{k})\sqrt{2}$

$a_{k+1}=a_{k}+2b_{k},b_{k+1}=a_{k}+b_{k}$(2).

$(1-\sqrt{2})^{k+1}=(1-\sqrt{2})^{k}(1-\sqrt{2})$

$=(c_{k}-d_{k}\sqrt{2})(1-\sqrt{2})=c_{k}\times 1-d_{k}\times \sqrt{2}-c_{k}\sqrt{2}-d_{k}\sqrt{2}\times (-\sqrt{2})$

$=c_{k}-d_{k}\sqrt{2}-c_{k}\sqrt{2}+2d_{k}=(c_{k}+2d_{k})-(c_{k}+d_{k})\sqrt{2}$

nên $c_{k+1}=c_{k}+2d_{k},d_{k+1}=c_{k}+d_{k}$ (3)

Từ (1), (2) và (3) ta suy ra $a_{k+1}=c_{k+1}$ và $b_{k+1}=d_{k+1}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

Vậy bài toán đã được chứng minh.

Luyện tập 3. Chứng minh $16^{n} – 15n – 1$ chia hết cho 225 với mọi n ∈ ℕ*.

Hướng dẫn trả lời:

+) Khi n = 1, ta có: 16$^{1}$ – 15n – 1 = 0 ⁝ 225.

Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $16^{k+1}– 15(k + 1) – 1$ chia hết cho 225.

Thật vậy, theo giả thiết quy nạp ta có: 16$^{k}$ – 15k – 1 chia hết cho 225.

Khi đó:

$16^{k+1} – 15(k + 1) – 1$

$= 16 \times  16^{k} – 15k – 16$

$= 16 \times  16^{k} – (240k – 225k)  – 16$

$= 16 \times  16^{k} – 240k + 225k  – 16$

$= 16 \times  16^{k} – 240k – 16 + 225k$

$= 16 (16^{k} – 15k – 1) + 225k

Vì $(16^{k} – 15k – 1)$ và 225k đều chia hết cho 225 nên $16 (16^{k} – 15k – 1) + 225k ⁝ 225$, do đó $16^{k+1} – 15(k + 1) – 1 ⁝ 225.$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

Bài tập

Bài tập 1. Cho $S_{n} = 1 + 2 + 2^{2} +... + 2^{n}$ và $T_{n} = 2^{n+1} – 1$, với n ∈ ℕ*.

a) So sánh S₁ và T₁; S₂ và T₂; S₃ và T₃.

b) Dự đoán công thức tính S_n và chứng minh bằng phương pháp quy nạp toán học

Hướng dẫn trả lời:

a) $S_{1} = 1 + 2^{1} = 3, S_{2} = 1 + 2 + 2^{2} = 7, S_{3} = 1 + 2 + 2^{2} + 2^{3} = 15.$

$T_{1} = 2^{1+1} – 1 = 3, T_{2} = 2^{2+1} – 1 = 7, T_{3} = 2^{3+1} – 1 = 15.$

Vậy S₁ = T₁; S₂ = T₂; S₃ = T₃.

b) Ta dự đoán S_n = T_n với n ∈ ℕ*.

• Khi n = 1, ta có: S₁ = T₁.

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $S_{k+1}=T_{k+1}$

Thật vậy, theo giả thiết quy nạp ta có: S_k = T_k.

Khi đó:

$S_{k} + 1 = 1 + 2 + 2^{2} +... + 2^{k} + 2^{k+1}$

$= S_{k} + 2^{k+1}$

$= T_{k} + 2^{k+1}$

$= (2^{k+1} – 1) + 2^{k+1}$

$= 2 \times  2^{k+1} – 1$

$= 2^{k+2} – 1$

$= 2^{(k + 1) + 1} – 1

=T_k + 1.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*. Vậy $S_{n} = T_{n} = 2^{n + 1} – 1$ với n ∈ ℕ*.

Bài tập 2. Cho $S_{n}=1+\frac{1}{2}+\frac{1}{2^{2}}+...+\frac{1}{2^{n}}$ và $Tn=2-\frac{1}{2^{n}}$ với n ∈ ℕ*.

a) So sánh S₁ và T₁; S₂ và T₂; S₃ và T₃.

b) Dự đoán công thức tính S_n và chứng minh bằng phương pháp quy nạp toán học.

Hướng dẫn trả lời:

a) $S_{1}=1+\frac{1}{2^{1}}=\frac{3}{2},S2=1+\frac{1}{2^{1}}+\frac{1}{2^{2}}=\frac{7}{4},S3=1+\frac{1}{2^{1}}+\frac{1}{2^{2}}+\frac{1}{2^{3}}=\frac{15}{8}$

$T_{1}=2-\frac{1}{2}=\frac{3}{2},T2=2-\frac{1}{2}=\frac{7}{4},T3=2-\frac{1}{3}=\frac{15}{8}$

Vậy S₁ = T₁; S₂ = T₂; S₃ = T₃.

b) Ta dự đoán S_n = T_n với n ∈ ℕ*.

• Khi n = 1, ta có: S₁ = T₁.

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $S_{k+1}=T_{k+1}$

Thật vậy, theo giả thiết quy nạp ta có: S_k = T_k.

Khi đó:

$S_{k+1}=1+\frac{1}{2}+\frac{1}{2^{2}}+...+\frac{1}{2^{k}}+\frac{1}{2^{k+1}}=Sk+\frac{1}{2^{k+1}}$

$=Tk+\frac{1}{2^{k+1}}=(2-\frac{1}{2^{k}})+\frac{1}{2^{k+1}}=2-(\frac{1}{2^{k}}-\frac{1}{2^{k+1}})$

$=2-(\frac{2}{2^{k+1}}-\frac{1}{2^{k+1}})=2-\frac{1}{2^{k+1}}=T_{k+1}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*. Vậy S_n = T_n = $2-\frac{1}{2^{n}}$ với n ∈ ℕ*.

Bài tập 3. Cho $S_{n}=\frac{1}{1\times 5}+\frac{1}{5\times 9}+\frac{1}{9\times 13}+...+\frac{1}{(4n-3)(4n+1)}$, với n ∈ ℕ*.

a) Tính S₁, S₂, S₃, S₄.

b) Dự đoán công thức tính S_n và chứng minh bằng phương pháp quy nạp toán học.

Hướng dẫn trả lời:

a) $S1=\frac{1}{1\times 5}=\frac{1}{5},S2=\frac{1}{1 \times 5}+\frac{1}{5 \times 9}=\frac{2}{9}$

$S3=\frac{1}{1 \times 5}+\frac{1}{5 \times 9}+\frac{1}{9 \times 13}=\frac{3}{13},S4=\frac{1}{1\times  5}+\frac{1}{5\times 9}+\frac{1}{9\times 13}+\frac{1}{13\times 17}=\frac{4}{17}$

b) Ta dự đoán $Sn=\frac{n}{4n+1}$

• Khi n = 1, ta có: $S1=\frac{1}{5}=\frac{1}{4 \times 1+1}$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $S_{k+1}=\frac{k+1}{4(k+1)+1}$

Thật vậy, theo giả thiết quy nạp ta có: $Sk=\frac{k}{4k+1}$

Khi đó:

$S=\frac{1}{1\times 5}+\frac{1}{5\times 9}+\frac{1}{9\times 13}+...+\frac{1}{(4n-3)(4n+1)}+\frac{1}{[4(k+1)-3][4(k+1)+1]}$

$=S_{k}+\frac{1}{[4(k+1)-3][4(k+1)+1]}=\frac{k}{4k+1}+\frac{1}{[4(k+1)-3][4(k+1)+1]}$

$=\frac{k}{4k+1}+\frac{1}{(4k+1)[4(k+1)+1]}=\frac{k[4(k+1)+1]}{(4k+1)[4(k+1)+1]}$

$=\frac{k(4k+5)}{(4k+1)[4(k+1)+1]}+\frac{1}{(4k+1)[4(k+1)+1]}$

$=\frac{4k^{2}+5k}{(4k+1)[4(k+1)+1]}+\frac{1}{(4k+1)[4(k+1)+1]}$

$=\frac{4k^{2}+5k+1}{(4k+1)[4(k+1)+1}=\frac{(4k+1)(k+1)}{(4k+1)[4(k+1)+1]}$

$=\frac{k+1}{4(k+1)+1}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*. Vậy $Sn=\frac{n}{4n+1}$ với n ∈ ℕ*.

Bài tập 4. Cho q là số thực khác 1. Chứng minh: $1 + q + q^{2} +... + q^{n-1}=\frac{1-q^{n}}{1-q}$ với n ∈ ℕ*.

Hướng dẫn trả lời:

• Khi n = 1, ta có: $1=\frac{1-q}{1-q}=\frac{1-q}{1-q^{1}}$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $1 + q + q^{2} +... + q^{k – 1} + q^{(k + 1) – 1} =  \frac{1-q^{k+1}}{1-q}$

Thật vậy, theo giả thiết quy nạp ta có: $1 + q + q^{2} +... + q^{k – 1} = \frac{1-q^{k}}{1-q}$

Khi đó:

$1 + q + q^{2} +... + q^{k – 1} + q^{(k + 1) – 1}$

$= (1 + q + q^{2} +... + q^{k – 1}) + q^{(k + 1) – 1}$

$=\frac{1-q^{k}}{1-q}+q^{(k+1)-1}=\frac{1-q^{k}}{1-q}+q^{k}$

$=\frac{1-q^{k}}{1-q}+\frac{q^{k}(1-q)}{1-q}=\frac{1-q^{k}}{1-q}+\frac{q^{k}-q^{k+1}}{1-q}$

$=\frac{(1-q^{k})+(q^{k}-q^{k+1})}{1-q}=\frac{1-q^{k+1}}{1-q}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

Bài tập 5. Chứng minh với mọi n ∈ ℕ*, ta có:

a) $4^{n} + 15n – 1$ chia hết cho 9;

b) $13^{n} – 1$ chia hết cho 6.

Hướng dẫn trả lời:

a)

• Khi n = 1, ta có: $4^{1} + 15 \times  1 – 1 = 18 ⁝ 9.$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $4^{k+1} + 15(k+1) – 1 ⁝ 9.$

Thật vậy, theo giả thiết quy nạp ta có: $4^{k} + 15k – 1 ⁝ 9.$

Khi đó:

$4^{k + 1} + 15(k+1) – 1$

$= 4 \times  4^{k} + 15k + 14$

$= 4\times  4^{k} + (60k – 45k) + (–4 + 18)$

$= (4 \times  4^{k} + 60k – 4) – 45k + 18$

$= 4 \times  (4^{k} + 15k – 1) – 45k + 18$

Vì $4^{k} + 15k – 1, 45k$ và 18 đều chia hết cho 9 nên $4 \times  (4^{k} + 15k – 1) – 45k + 18 ⁝ 9,$ do đó $4^{k + 1} + 15(k+1) – 1 ⁝ 9.$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

b)

• Khi n = 1, ta có: $13^{1} – 1 = 12 ⁝ 6.$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $13^{k + 1} – 1 ⁝ 6$.

Thật vậy, theo giả thiết quy nạp ta có: $13^{k} – 1 ⁝ 6.$

Khi đó:

$13^{k + 1} – 1$

$= 13 \times  13^{k} – 1$

$= 13 \times  13^{k} – 13 + 12$

$= 13 \times  (13^{k} – 1) + 12$

Vì $13^{k} – 1$ và 12 đều chia hết cho 6 nên $13 \times  (13^{k} – 1) + 12 ⁝ 6$, do đó $13^{k + 1} – 1 ⁝ 6.$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

Bài tập 6. Chứng minh $n^{n} > (n + 1)^{n – 1}$ với n ∈ ℕ*, n ≥ 2.

Hướng dẫn trả lời:

• Khi n = 2, ta có: $2^{2} > (2 + 1)^{2 – 1}  \Leftrightarrow 4 > 3.$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý (k ≥ 2) mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: $(k + 1)^{k + 1} > [(k+1) + 1]^{(k + 1) – 1}$.

Thật vậy, theo giả thiết quy nạp ta có: $k^{k} > (k + 1)^{k – 1}$.

Suy ra: $k^{k} \times  (k + 1)^{k + 1} > (k + 1)^{k – 1} \times  (k + 1)^{k + 1}$

$\Rightarrow  k^{k} \times  (k + 1)^{k + 1} > (k + 1)^{2k}$

$ \Rightarrow k^{k} \times  (k + 1)^{k + 1} > [(k + 1)^{2}]^{k}$

$\Rightarrow  k^{k} \times  (k + 1)^{k + 1} > (k^{2} + 2k + 1)^{k} > (k^{2} + 2k)^{k} = [k(k + 2)]^{k}= k^{k} . (k + 2)^{k}$

$\Rightarrow  (k + 1)^{k + 1} > (k + 2)^{k} = (k + 2)^{(k + 1) – 1}$

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề P(n) đúng với mọi n ∈ ℕ*, n ≥ 2.

Bài tập 7. Chứng minh $a^{n} – b^{n} = (a – b)(a^{n – 1} + a^{n – 2}b + ... + ab^{n –2} + b^{n – 1})$ với n ∈ ℕ*.

Hướng dẫn trả lời:

• Khi n = 1, ta có: $a^{1} – b^{1} = a – b.$

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là:

$a^{k + 1} – b^{k + 1} = (a – b)[a^{(k + 1) – 1} + a^{(k + 1) – 2}b + ... + ab^{(k + 1) –2} + b^{(k + 1) – 1}]$

Thật vậy, theo giả thiết quy nạp ta có:

$a^{k} – b^{k} = (a – b)(a^{k – 1} + a^{k – 2}b + ... + ab^{k –2 }+ b^{k – 1})$

Khi đó:

$a^{k + 1} – b^{k + 1}$

$= a \times  a^{k} – b \times  b^{k}$

$= a \times  a^{k} – a \times  b^{k} + a \times  b^{k} – b \times  b^{k}$

$= a \times  (a^{k} – b^{k}) + b^{k} \times  (a – b)$

$= a v (a – b)(a^{k – 1} + a^{k – 2}b + ... + ab^{k –2 }+ b^{k – 1}) + b^{k} \times  (a – b)$

$= (a – b) \times  a \times  (a^{k – 1} + a^{k – 2}b + ... + ab^{k –2} + b^{k – 1}) + (a – b) \times  b^{k}$

$= (a – b)(a \times  a^{k – 1} + a \times  a^{k – 2}b + ... + a \times  ab^{k – 2} + a \times  b^{k – 1}) + (a – b) \times  b^{k}$

$= (a – b)[a^{1 + (k – 1)} + a^{1 + (k – 2)}b + ... + a^{2}b^{k – 2} + a \times  b^{k – 1}) + (a – b) \times  b^{k}$

$= (a – b)[a^{(k + 1) – 1} + a^{(k + 1) – 2}b + ... + a^{2}b^{(k + 1) – 3} + ab^{(k + 1) –2}] + (a – b) \times  b^{(k + 1) – 1}$

$= (a – b)[a^{(k + 1) – 1} + a^{(k + 1) – 2}b + ... + ab^{(k + 1) –2} + b^{(k + 1) – 1}]$.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề P(n) đúng với mọi n ∈ ℕ*.

Bài tập 8. Cho tam giác đều màu xanh (Hình thứ nhất).

a) Nêu quy luật chọn tam giác đều màu trắng ở Hình thứ hai.

b) Nêu quy luật chọn các tam giác đều màu trắng ở Hình thứ ba.

c) Nêu quy luật tiếp tục chọn các tam giác đều màu trắng từ Hình thứ tư và các tam giác đều màu trắng ở những hình sau đó.

d) Tinh số tam giác đều màu xanh lần lượt trong các Hình thứ nhất, Hình thú hai, Hình thứ ba.

e) Dự đoán số tam giác đều màu xanh trong Hình thứ n. Chứng minh kết quả đó bằng phương pháp quy nạp toán học.

Hướng dẫn trả lời:

a) Tam giác đều màu trắng ở Hình thứ hai có đỉnh là trung điểm các cạnh của tam giác đều màu xanh ở hình thứ nhất.

b) Giữ nguyên tam giác đều màu trắng ở Hình thứ hai, với mỗi tam giác đều màu xanh ở Hình thứ hai, ta lại chọn các tam giác đều màu trắng như cách ở Hình thứ nhất.

c) Giữ nguyên các tam giác đều màu trắng ở Hình thứ ba, với mỗi tam giác đều màu xanh ở Hình thứ ba, ta lại chọn các tam giác đều màu trắng như cách ở Hình thứ nhất.

Như vậy, ta có quy luật chọn các tam giác đều màu trắng ở hình thứ n:

Giữ nguyên các tam giác đều màu trắng ở Hình thứ n – 1, với mỗi tam giác đều màu xanh ở Hình thứ n – 1, ta lại chọn các tam giác đều màu trắng như cách ở Hình thứ nhất.

d) Số tam giác đều màu xanh ở Hình thứ nhất là: 1.

Số tam giác đều màu xanh ở Hình thứ hai là: 3.

Số tam giác đều màu xanh ở Hình thứ ba là: 9.

e) Dự đoán số tam giác đều màu xanh ở Hình thứ n là: $3^{n – 1}$.

Xét mệnh đề P(n): "Số tam giác đều màu xanh ở Hình thứ n là $3^{n – 1}$ với n ∈ ℕ*".

Chứng minh:

• Khi n = 1, ta có: Số tam giác đều màu xanh ở Hình thứ nhất là: 1.

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là:

Số tam giác đều màu xanh ở Hình thứ (k + 1) là $3^{(k + 1) –1}$.

Thật vậy, theo giả thiết quy nạp ta có:

Số tam giác đều màu xanh ở Hình thứ k là $3^{k –1}$.

Vì với cách chọn như trên, mỗi tam giác đều màu xanh sẽ tạo ta 3 tam giác đều màu xanh mới ở hình tiếp theo nên từ $3^{k – 1}$ tam giác đều màu xanh ở Hình thứ k sẽ cho ta 3 x $3^{k – 1} = 3k = 3^{(k + 1) – 1}$ tam giác đều màu xanh ở Hình thứ (k + 1).

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề P(n) đúng với mọi n ∈ ℕ*.

Bài tập 9. Quan sát hình 6.

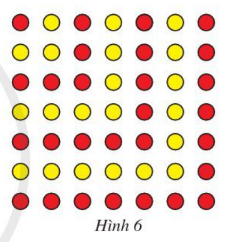
a) Nêu quy luật sắp xếp các chấm đỏ và vàng xen kẽ nhau khi xếp các chấm đó từ góc trên bên trái xuống góc dưới bên phải (tạo thành hình vuông).

b) Giả sử hình vuông thứ n có mỗi cạnh chứa n chấm. Tinh tổng số chấm được xếp trong hình vuông (kể cả trên cạnh). Chứng minh kết quả đó bằng phương pháp quy nạp toán học.

Hướng dẫn trả lời:

a) Số chấm tăng thêm sau mỗi lượt xếp (kể từ lượt đầu tiên) là các số lẻ liên tiếp bắt đầu từ 1.

b) Vì ở hình vuông thứ n có mỗi cạnh chứa n chấm nên tổng số chấm là n$^{2}$.

Mặt khác, theo cách sắp xếp trên ta lại có tổng số chấm là: 1 + 3 + 5 + ... + (2n – 1).

Như vậy ta sẽ chứng minh mệnh đề

P(n): "1 + 3 + 5 + ... + (2n – 1) = n$^{2}$ với mọi n ∈ ℕ*".

+) Khi n = 1, ta có: 1 = 1$^{2}$.

Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: 1 + 3 + 5 + ... + (2k – 1) + [2(k+1) – 1] = (k + 1)$^{2}$.

Thật vậy, theo giả thiết quy nạp ta có: 1 + 3 + 5 + ... + (2k – 1) = k$^{2}$.

Khi đó:

1 + 3 + 5 + ... + (2k – 1) + [2(k+1) – 1]

= [1 + 3 + 5 + ... + (2k – 1)] + [2(k+1) – 1]

= k$^{2}$ + [2(k+1) – 1]

= k$^{2}$ + (2k + 2 –1)

= k$^{2}$ + 2k + 1

= (k + 1)$^{2}$.

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề P(n) đúng với mọi n ∈ ℕ*.

Bài tập 10. Giả sử năm đầu tiên, cô Hạnh gửi vào ngân hàng A (đồng) với lãi suất r%/năm. Hết năm đầu tiên, cô Hạnh không rút tiền ra và gửi thêm A (đồng) nữa. Hết năm thứ hai, cô Hạnh cũng không rút tiền ra và lại gửi thêm A (đồng) nữa. Cứ tiếp tục như vậy cho những năm sau. Chứng minh số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là $Tn=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{n}-1]$ (đồng), nếu trong khoảng thời gian này lãi suất không thay đổi.

Hướng dẫn trả lời:

Xét mệnh đề P(x): "Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là  (đồng) (n ∈ ℕ*)".

• Khi n = 1:

Số tiền lãi người đó nhận được là: A x r% = $\frac{A\times r}{100}$ (đồng).

Số tiền nhận được (bao gồm cả vốn lẫn lãi) là:

$A+\frac{A\times r}{100}=\frac{A(100+r)}{100}=\frac{A(100+r)}{r}\times \frac{r}{100}$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})-1]$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})-1]$ (đồng)

Vậy mệnh đề đúng với n = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau (k +1) (năm) là 

$T_{k+1}=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k+1}-1]$ (đồng)

Thật vậy, theo giả thiết quy nạp ta có:

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau k (năm) là:

$Tk=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k}-1]$ (đồng)

Vì cô Hạnh không rút tiền ra và lại gửi thêm A (đồng) nữa nên:

Số tiền vốn của cô Hạnh sau (k + 1) năm là: Tk + A (đồng).

Số tiền lãi cô Hạnh nhận được sau (k + 1) (năm) là: (Tk + A) x r% (đồng).

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau (k + 1) (năm) là: (Tk + A) + (Tk + A) x r%

$=(Tk+A)+(Tk+A)\times \frac{r}{100}=(Tk+A)(1+\frac{r}{100})$

={$\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k}-1]+A$} x $(1+\frac{r}{100})$

$=\frac{A(100+r}{r}[(1+\frac{r}{100})^{k}-1](1+\frac{r}{100})+A(1+\frac{r}{100})$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k+1}-(1+\frac{r}{100})]+A\times \frac{100+r}{100}$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k+1}-(1+\frac{r}{100})]+A\times \frac{100+r}{r}\times \frac{r}{100}$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k+1}-(1+\frac{r}{100})+\frac{r}{100}]$

$=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{k+1}-1]=T_{k+1}$ (đồng)

Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*. Từ đó ta có điều phải chứng minh.

Bài tập 11. Một người gửi số tiền A (đồng) vào ngân hàng. Biểu lãi suất của ngân hàng như sau: Chia mỗi năm thành m kì hạn và lãi suất r%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thi cứ sau mỗi kì hạn, số tiển lãi sẽ được nhập vào vốn ban đầu. Chứng minh số tiền nhận được (bao gồm cả vốn lẫn lãi) sau n (năm) gửi là $Sn=A(1+\frac{r}{100m})^{m\times n}$ (đồng), nếu trong khoảng thời gian này người gửi không rút tiền ra và lãi suất không thay đổi.

Hướng dẫn trả lời:

Xét mệnh đề P(x): "Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau x (kì hạn) gửi là $Sn=A(1+\frac{r}{100m)})^{x}$ (đồng) (x ∈ ℕ*)".

Vì một năm có m kì hạn nên lãi suất mỗi kì hạn là $\frac{r%}{m}=\frac{r}{100m}$

• Khi x = 1:

Số tiền lãi người đó nhận được là: A x $\frac{r}{100m}$ (đồng).

Số tiền nhận được (bao gồm cả vốn lẫn lãi) là:

A+A x $\frac{r}{100m}=A(1+\frac{r}{100m})=A(1+\frac{r}{100m})^{1}$ (đồng)

Vậy mệnh đề đúng với x = 1.

• Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau (k + 1) (kì hạn) gửi là $Sn=A(1+\frac{r}{100m})^{k+1}$ (đồng).

Thật vậy, theo giả thiết quy nạp ta có:

Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau k (kì hạn) gửi là $Sn=A(1+\frac{r}{100m})^{k}$ (đồng).

Vì sau mỗi kì hạn, số tiển lãi sẽ được nhập vào vốn ban đầu nên số tiền lại ở kì hạn thứ (k + 1) là: $A(1+\frac{r}{100m})^{k}$ x $\frac{r}{100m}$ (đồng).

Suy ra số tiền nhận được (bao gồm cả vốn lẫn lãi) là:

$A(1+\frac{r}{100m})^{k}+A(1+\frac{r}{100m})^{k}$ x $\frac{r}{100m}$

$=A(1+\frac{r}{100m})^{k}(1+\frac{r}{100m})=A(1+\frac{r}{100m})^{k+1}$ (đồng)

Vậy mệnh đề cũng đúng với x = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi x ∈ ℕ*.

Sau n (năm) thì số kì hạn người đó đã gửi là: m x n (kì hạn).

Do đó, số tiền nhận được (bao gồm cả vốn lẫn lãi) sau n (năm) gửi là:

$Sn=A(1+\frac{r}{100m})^{m\times n}$ (đồng)