Tải giáo án Powerpoint Toán 8 cánh diều Chương 5 Bài 6: Hình thoi

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Họa tiết trên vải ở Hình 55 gợi nên hình ảnh của hìn thoi.

Hình thoi có những tính chất gì? Có những dấu hiệu nào để   nhận biết một hình bình hành là hình thoi?

CHƯƠNG V. ĐỊNH LÍ PYTHAGORE. TỨ GIÁC

BÀI 6: HÌNH THOI

NỘI DUNG BÀI HỌC

Định nghĩa

Tính chất

Dấu hiệu nhận biết

1. ĐỊNH NGHĨA

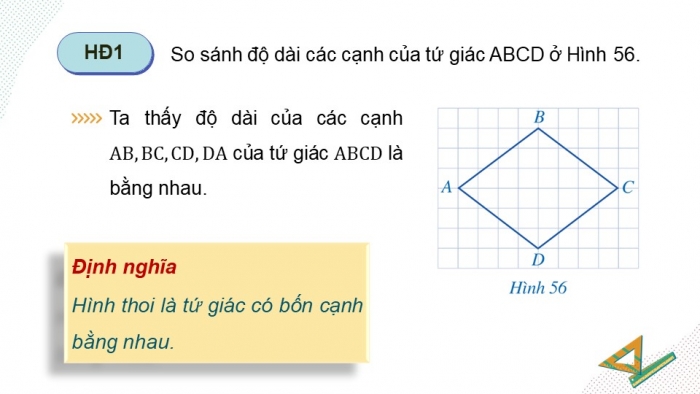
HĐ1

So sánh độ dài các cạnh của tứ giác ABCD ở Hình 56.

Ta thấy độ dài của các cạnh  của tứ giác  là bằng nhau.

Định nghĩa

Hình thoi là tứ giác có bốn cạnh bằng nhau.

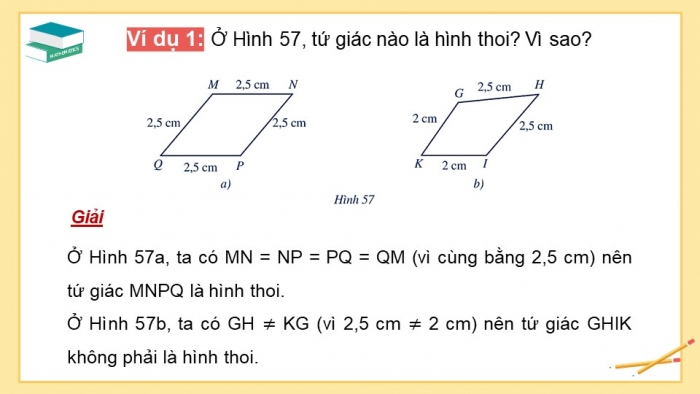
Ví dụ 1:

Ở Hình 57, tứ giác nào là hình thoi? Vì sao?

Giải

Ở Hình 57a, ta có MN = NP = PQ = QM (vì cùng bằng 2,5 cm) nên tứ giác MNPQ là hình thoi.

Ở Hình 57b, ta có GH  KG (vì 2,5 cm  2 cm) nên tứ giác GHIK không phải là hình thoi.

2. TÍNH CHẤT

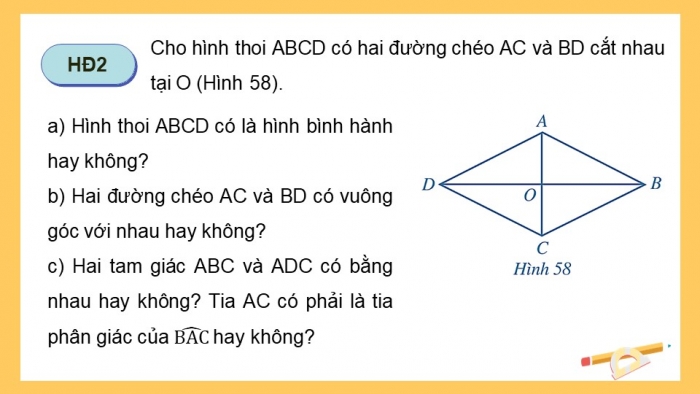
HĐ2

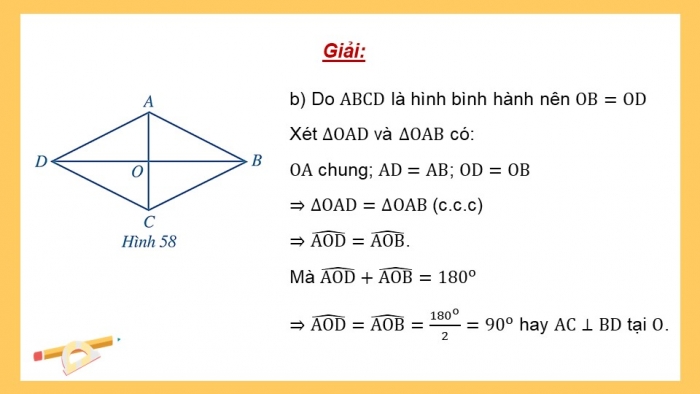
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

1. a) Hình thoi ABCD có là hình bình hành hay không?
2. b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
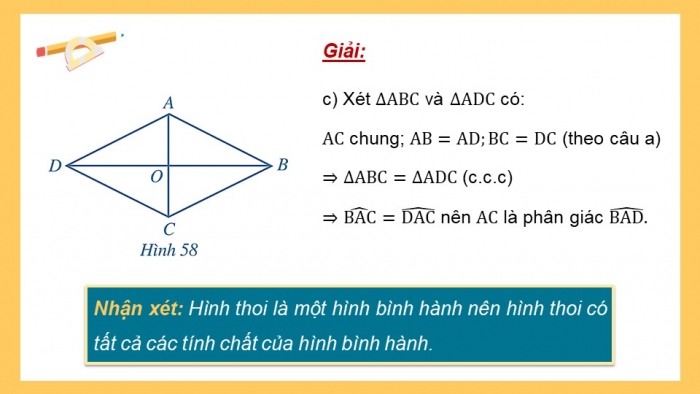
3. c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của hay không?

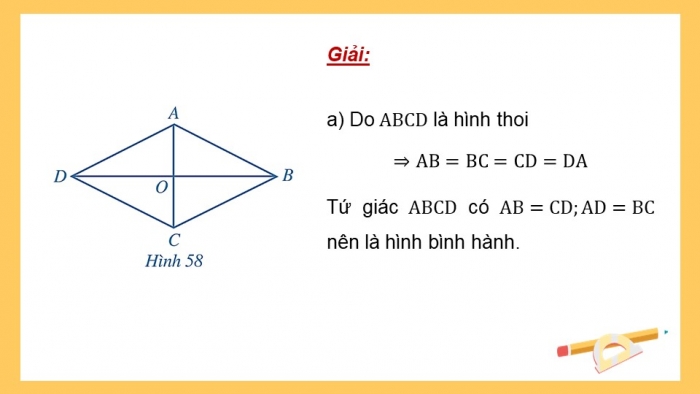
Giải:

1. a) Do là hình thoi

Tứ giác  có  nên là hình bình hành.

1. b) Do là hình bình hành nên

Xét  và  có:

 chung; ;

 (c.c.c)

 .

Mà

  hay  tại .

1. c) Xét và có:

 chung;  (theo câu a)

 (c.c.c)

 nên  là phân giác

Nhận xét: Hình thoi là một hình bình hành nên hình thoi có tất cả các tính chất của hình bình hành.

ĐỊNH LÍ

Trong một hình thoi:

1. a) Các cạnh đối song song;
2. b) Các góc đối bằng nhau;
3. c) Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;
4. d) Hai đường chéo là các đường phân giác của các góc ở đỉnh.

Ví dụ 2:

Cho hình thoi  có hai đường chéo  và  cắt nhau tại

 (Hình 59). Tính độ dài của

Giải

Do  là hình thoi nên O là trung điểm của hai đường chéo

Ta có (vì  là hình thoi) nên tam giác OAB vuông tại O. Áp dụng định lí Pythagore, ta có:

hay

Luyện tập 1

Cho hình thoi ABCD có . Chứng minh tam giác ABD là tam giác đều.

Giải

Ta có  là hình thoi, ;   cân tại .

Lại có  là phân giác  (tính chất hình thoi)

Vậy  là tam giác cân có một góc  nên là tam giác đều.

3. DẤU HIỆU NHẬN BIẾT

HĐ3

1. a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?
2. b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 60).

• Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
• ABCD có phải là hình thoi hay không?

Giải

1. a) Do là hình bình hành nên và .

Mà  . Vậy  là hình thoi.

1. b) Do là hình bình hành

 Hai đường chéo  và  cắt nhau tại trung điểm mỗi đường.

  tại trung điểm  của   là trung trực của .

Vì  là đường trục trực của   

Theo câu a, hình bình hành  có hai cạnh kề  và  bằng nhau nên là hình thoi.

DẤU HIỆU NHẬN BIẾT

• Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

Ví dụ 3:

Cho tam giác ABC vuông tại A. Các điểm M, N lần lượt thuộc tia đối của tia AB, AC sao cho AM = AB, AN = AC. Chứng minh tứ giác BCMN là hình thoi.

Giải

Tứ giác BCMN có A là trung điểm của cả hai đường chéo BM và CN nên BCMN là hình bình hành.

Do tam giác ABC vuông tại A nên  

hay BM  CN.

Hình bình hành BCMN có hai đường chéo BM và CN vuông góc với nhau nên BCMN là hình thoi.

Luyện tập 2