Giải chuyên đề học tập Toán 10 KNTT bài 5: Elip

Câu hỏi khởi động: Một hành tinh trong hệ Mặt Trời chuyển động theo một quỹ đạo hình elip nhận tâm Mặt Trời là một tiêu điểm. Khoảng cách lớn nhất và nhỏ nhất từ Trái Đất đến tâm Mặt Trời tương ứng khoảng 152.10^8 km và 147.10^8 km (theo nssdc.gsfc.nasa.gov). Liệu có lập được phương trình chính tắc của elip là quỹ đạo của Trái Đất?

Có lập được phương trình chính tắc 

Ta gọi khoảng cách lớn nhất và nhỏ nhất từ Trái Đất đến tâm Mặt Trời làm trục, tại các điểm cắt gọi là tiêu cự. Lấy mặt trời làm tiêu điểm.

Luyện tập 1: Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6

Gọi phương trình chính tắc của elip đã cho là 

Theo đề bài ta có:
Độ dài trục lớn bằng 10, suy ra 2a=10 => a=5

Elip có một tiêu cự bằng 6, suy ra 2c=6 => c=3

Suy ra b^2=a^2-c^2=5^2-3^2=16

Vậy phương trình chính tắc của elip là: 

Luyện tập 2: Cho đường tròn có phuong trình x^2 + y^2 = a^2 và số (0 < k < 1). Với mỗi điểm M(x0; y0) thuộc đường tròn, gọi H(x0; 0) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho HN = kHM (H.3.5).

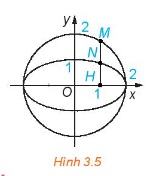
a, Tính toạ độ của N theo x0; y0; k.

b, Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên elip có phương trình chính tắc

a,  Gọi toạ độ của N là (xN; yN­).

Khi đó: 

Vì HN = kHM nên 

Nên: 

b, Khi M thay đổi trên đường tròn ta luôn có Xo^2 + Yo^2=a^2

Do đó:

Vậy N luôn thay đổi trên elip có phương trình chính tắc

2.BÁN KÍNH QUA TIÊU CỰ, TÂM SAI VÀ ĐƯỜNG CHUẨN

Hoạt động 2: Cho hau tiêu điểm F1(-c;0), F2(c;0) và độ dài trục lớn bằng 2a và điểm M(x;y)

a, Tính MF1^2 - MF2^2

b, Khi điểm M thuộc elip (MF1+MF2=2a). Tính MF1-MF2; MF1;MF2

a, MF1^2 – MF2^2 = (x^2 + 2cx + c^2 + y^2) – (x^2 – 2cx + c^2 + y^2) = 4cx.

b,  MF12 – MF22 = 4cx

MF1 + MF2 = 2a và MF1 – MF2 = 2c/a(x) 

Suy ra:

Từ MF1 + MF2 = 2a và MF1 – MF2 =2c/ax

Suy ra:

Luyện tập 3: Cho elip  điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?

Có a^2 = 36, suy ra a = 6.

c = √a^2−^=√36−20=√16=4.

Gọi toạ độ của M là (x; y).

Ta xét khoảng cách từ M đến F1.

Theo công thức độ dài bán kính qua tiêu ta có MF1 = 6 +4x/6 = 6+ 2x/3

Mặt khác, vì M thuộc elip nên –6 ≤ x ≤ 6

Vậy 2=< MF1=< 10

Vậy độ dài MF1 nhỏ nhất bằng 2 khi M có hoành độ bằng –6, lớn nhất bằng 10 khi M có hoành độ bằng 6.

Vận dụng 1: Với thông tin được đưa ra tronh tình huống mở đầu, lập phương trình chính tắc của elip quỹ đạo của trái đất, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với 10^6 trên thực tế

Gọi phương trình chính tắc của elip là 

Giả sử Trái Đất có toạ độ là điểm M(x; y) và tâm Mặt Trời trùng với tiêu điểm F1.

Khi đó, khoảng cách lớn nhất và nhỏ nhất từ Trái Đất đến tâm Mặt Trời lần lượt là a + c và a – c.

Theo đề bài ta có: a + c = 152 và a – c = 147.

Suy ra a = 149,5 và c = 2,5.

Suy ra b^2 = a^2 – c^2 = 149,5^2 – 2,5^2 = 22344.

Vậy phương trình chính tắc của elip là

Hoạt động 3: Cho elip có phương trình chính tắc với các tiêu điểm F1(–c; 0), F2(c; 0), ở đây Xét các đường thẳng Với điểm M(x; y) thuộc elip, tính các tỉ số theo a và c

Viết lại phương trình đường thẳng Δ1 ở dạng: x+0y+a^2/c=0.

Với mỗi điểm M(x; y) thuộc elip, ta có:

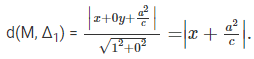
 Do MF1=a+cx/a >0 Nên MF1 =

Suy ra: 

Luyện tập 4: Cho elip có phương trình chính tắc 

Tìm tâm sai và các đường chuẩn của elip. Tính các bán kính qua tiêu của điểm  thuộc elip và có hoành độ bằng –2.

Có a^2 = 36, b^2 = 25, suy ra a = 6, b = 5.

Suy ra: 

Tâm sai của elip là e = , các đường chuẩn của elip là :

Các bán kính qua tiêu của điểm  thuộc elip và có hoành độ bằng –2 là:

Vận dụng 2: Mặt Trăng chuyển động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu điểm. Các khoảng cách lớn nhất và nhỏ nhất từ các vị trí của Mặt Trăng đến tâm Trái Đất tương ứng là 400000 km và 363000 km.

Ta có a= 400000, b= 363000

Suy ra c= 168020,8

Vậy tâm sai của elip là e=0,42

BÀI TẬP

3.1. Cho elip 

a) Xác định đỉnh và độ dài các trục của elip.

b) Xác định tâm sai và các đường chuẩn của elip.

c) Tính các bán kính qua tiêu của điểm M thuộc elip, biết điểm M có hoành độ bằng –3.

a, Có a^2=12, b^2=4 => a=căn 12=2 căn 3; b=2

Toạ độ các đỉnh của elip là 

Độ dài trục lớn của elip là 2a = 2.2√3=4√3.

Độ dài trục nhỏ của elip là 2b = 2.2 = 4.

b, 

Tâm sai của elip là 

Các đường của elip là:

C, Các bán kính qua tiêu điểm thuộc elip và có hoành độ bằng -3 là:

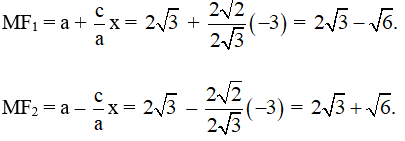
3.2. Viết phương trình chính tắc của elip trong mỗi trường hợp sau:

a) Độ dài trục lớn bằng 8, tiêu cự bằng 6;

b) Độ dài trục lớn bằng 8 và tâm sai bằng  căn 3/2

a, Gọi phương trình chính tắc của elip đã cho là 

Theo đề bài ta có:

Độ dài trục lớn bằng 8, suy ra 2a = 8, suy ra a = 4.

Tiêu cự bằng 6, suy ra 2c = 6 hay c = 3,

suy ra b^2 = a^2 – c^2 = 4^2 – 3^2 = 7.

Vậy phương trình chính tắc của elip đã cho là

b, Gọi phương trình chính tắc của elip đã cho là 

Theo đề bài ta có:

Độ dài trục lớn bằng 8, suy ra 2a = 8, suy ra a = 4.

 Elip có tâm sai bằng √3/2 , 

Suy ra: 

Vậy phương trình chính tắc của elip đã cho là 

3.3. Cho elip  

a, Qua tiêu điểm của elip vẽ đường thẳng vuông góc với trục Ox, cắt elip tại hai điểm A và B. Tính độ dài đoạn thẳng AB.

b, Tìm điểm M trên elip sao cho MF1 = 2MF2 với F1 và F2 là hai tiêu điểm của elip (hoành độ của F1 âm).

Ta có : 

a,  Giả sử A nằm phía trên còn B nằm phía dưới trục Ox.

Khi đó toạ độ của A có dạng (c; yA) hay (2; yA) với yA > 0;

toạ độ của B có dạng (c; yB) hay (2; yB) với yB > 0.

Vì A thuộc elip nên

Vì B thuộc elip nên 

b, Gọi toạ độ của M là (x; y). Theo công thức bán kính qua tiêu ta có:

Do đó: MF1 = 2MF2

Vậy 

3.4. Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip (H.3.8). Do đó, đường tròn phụ là đường tròn lớn nhất có thể nằm bên trong một hình elip. Tìm phương trình đường tròn phụ của elip  và chứng minh rằng, nếu điểm M(x0; y0) thuộc elip thì điểm   thuộc đường tròn phụ.

Vì đường tròn phụ có đường kính là trục nhỏ của elip nên có tâm là O(0; 0) và bán kính b.

Vậy phương trình đường tròn phụ là: X^2+Y^2=B^2

Có M(x0; y0) thuộc elip nên 

Xét điểm , ta có:

Vậy toạ độ điểm N thoả mãn phương trình đường tròn phụ, do đó điểm N thuộc đường tròn phụ.

3.5. Với tâm sai khoảng 0,244, quỹ đạo elip của sao Diêm Vương "dẹt" hơn so với quỹ đạo của tám hành tinh trong hệ Mặt Trời (xem Em có biết? ở cuối bài). Nửa độ dài trục lớn của elip quỹ đạo là khoảng 590635.10^6 km. Tìm khoảng cách gần nhất và khoảng cách xa nhất giữa sao Diêm Vương và tâm Mặt Trời (tiêu điểm của quỹ đạo)

Chọn hệ trục toạ độ sao cho tâm Mặt Trời trùng với tiêu điểm F1 của elip, đơn vị trên các trục là kilômét.

Giả sử phương trình chính tắc của quỹ đạo elip này là 

Theo đề bài, ta có:

Nửa độ dài trục lớn của elip quỹ đạo là khoảng 590635.106 km, suy ra a = 590635.10^6.

Elip có yâm sai khoảng 0,244 => c/a= 0,244

=>  c = 0,244.a = 144114,94.10^6

Giả sử sao Diêm Vương có toạ độ là M(x; y).

Khoảng cách giữa sao Diêm Vương và tâm Mặt Trời là MF1.

Vậy khoảng cách gần nhất và khoảng cách xa nhất giữa sao Diêm Vương và tâm Mặt Trời lần lượt là 46520,06.10^6 km và 734749,94.10^6 km.

3.6. Một phòng thì thầm có trần vòm elip với hai tiêu điểm ở độ cao 1,6 m (so với mặt sàn) và cách nhau 16 m. Đỉnh của mái vòm cao 7,6 m (H.3.9). Hỏi âm thanh thì thầm từ một tiêu điểm thì sau bao nhiêu giây đến được tiêu điểm kia? Biết vận tốc âm thanh là 343,2 m/s và làm tròn đáp số tới 4 chữ số sau dấu phẩy.

Giả sử phương trình chính tắc của elip này là 

Dựa vào hình vẽ ta thấy: 2c = 16  ⇒c = 8.

b = 7,6 – 1,6 = 6 ⇒⇒  a =

Âm thanh đi từ một tiêu điểm qua điểm M(x; y) trên trần vòm rồi đến tiêu điểm kia. Do đó quãng đường mà âm thanh đã đi là: MF1 + MF2.

Theo công thức bán kính qua tiêu ta có: 

 Quãng đường âm thanh đã đi là:

Thời gian âm thanh đã đi là:≈ 0,0583 (s).

Vậy âm thanh thì thầm từ một tiêu điểm thì sau khoảng 0,0583 giây sẽ đến được tiêu điểm kia.