Hướng dẫn giải nhanh vật lí 11 CTST bài 3: Vận tốc, gia tốc trong chuyển động điều hòa

I. THẾ NĂNG TRONG DAO ĐỘNG ĐIỀU HÒA

Thảo luận 1 trang 22 sgk vật lý 11 ctst

Dựa vào công thức (3.2) và Hình 3.2, mô tả sự thay đổi của thế năng trong một chu kì dao động của vật.

Đáp án:

Thế năng của vật đạt cực đại khi ở vị trí hai biên và đạt cực tiểu ở vị trí cân bằng. Thế năng giảm dần từ giá trị lớn nhất về 0 khi vật di chuyển từ vị trí biên đến vị trí cân bằng và ngược lại.

Thảo luận 2 trang 23 sgk vật lý 11 ctst

So sánh chu kì, tần số biến thiên của thế năng với chu kì, tần số dao động của vật.

Đáp án:

Tần số của thế năng gấp hai lần tần số dao động của vật và chu kì bằng một nửa chu kì dao động của vật.

Luyện tập trang 23 sgk vật lý 11 ctst

Một số toà nhà cao tầng sử dụng các con lắc nặng trong bộ giảm chấn khối lượng (mass damper) để giảm thiểu sự rung động gây ra bởi gió hay những cơn địa chấn nhỏ. Giả sử vật nặng của con lắc có khối lượng 3,0.10$^{5}$kg, thực hiện dao động điều hoà với với tần số 15 Hz với biên độ dao động là 15 cm. Hãy xác định thế năng cực đại của hệ con lắc trong bộ giảm chấn khối lượng.

Đáp án:

$W_{tmax}$  = ½.mω$^{2}$A$^{2}$ = ½.3,0.10$^{5}$.(2π.15)$^{2}$.0,15$^{2}$ = 3037500π$^{2}$(J)

II. ĐỘNG NĂNG TRONG DAO ĐỘNG ĐIỀU HÒA

Thảo luận 3 trang 23 sgk vật lý 11 ctst

Dựa vào công thức (3.5) và Hình 3.3, mô tả sự thay đổi của động năng trong một chu kì dao động của vật.

Đáp án:

Động năng của vật đạt cực đại ½.mω$^{2}$A$^{2}$ ở vị trí cân bằng và đạt cực tiểu là 0 ở vị trí hai biên.

Trong một chu kì động năng của vật đạt cực đại ở vị trí cân bằng và giảm dần bằng 0 ở vị trí hai biên.

Thảo luận 4 trang 24 sgk vật lý 11 ctst

So sánh pha dao động của thế năng và động năng khi vật dao động điều hòa.

Đáp án:

Thế năng và động năng ngược pha nhau.

Luyện tập trang 24 sgk vật lý 11 ctst

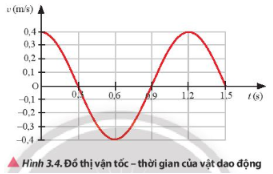
Một vật có khối lượng 2 kg dao động điều hoà có đồ thị vận tốc – thời gian như Hình 3.4. Xác định tốc độ cực đại và động năng cực đại của vật trong quá trình dao động.

Đáp án:

$v_{max}$ = 0,4 m/s

Động năng cực đại của vật trong quá trình dao động là

$W_{đ}$ = ½.mv$^{2}$ = ½.2.0,4$^{2}$ = 0,16 (J)

III. SỰ CHUYỂN HÓA NĂNG LƯỢNG VÀ BẢO TOÀN CƠ NĂNG TRONG DAO ĐỘNG ĐIỀU HÒA

Thảo luận 5 trang 24 sgk vật lý 11 ctst

Quan sát Hình 3.5 và mô tả sự thay đổi của động năng và thế năng khi vật dao động di chuyển từ biên âm đến biên dương.

Đáp án:

Khi vật ở biên âm, Wt cực đại còn $W_{đ}$ bằng 0.

Khi vật di chuyển từ biến âm về vị trí cân bằng, $W_{t}$ giảm trong khi $W_{đ}$ tăng.

Khi vật đi qua vị trí cân bằng, $W_{t}$ bằng 0 và $W_{đ}$ cực đại.

Khi vật di chuyển từ vị trí cân bằng ra biên dương, $W_{t}$ tăng trong khi $W_{đ}$ giảm.

Khi vật ở biên cương, $W_{t}$ cực đại còn Wđ bằng 0.

Thảo luận 6 trang 25 sgk vật lý 11 ctst

Quan sát Hình 3.5 và 3.6, nhận xét về độ lớn của động năng, thế năng và cơ năng trong quá trình dao động điều hòa của vật.

Đáp án:

Khi thế năng tăng thì động năng giảm, cơ năng không đổi và luôn bằng tổng giá trị của động năng và thế năng 

W = $W_{đmax}$ = $W_{tmax}$ = $W_{đ}$ + $W_{t}$ = ½.mω$^{2}$A$^{2}$

Thảo luận 7 trang 25 sgk vật lý 11 ctst

Dựa vào biểu thức (3.2) và (3.5), hãy thiết lập biểu thức (3.7).

Đáp án:

Ta có: $W_{t}$ = ½.mω$^{2}$A$^{2}$cos$^{2}$(ωt+φ)

$W_{đ}$ = ½.mv$^{2}$ = ½.mω$^{2}$A$^{2}$sin$^{2}$(ωt+φ)

⇒W = $W_{t}$ + $W_{đ}$ = ½.mω$^{2}$A$^{2}$cos$^{2}$(ωt+φ) + ½.mω$^{2}$A$^{2}$sin$^{2}$(ωt+φ)

⇒W = ½.mω$^{2}$A$^{2}$(cos$^{2}$(ωt+φ)+sin$^{2}$(ωt+φ)

Mà cos$^{2}$(ωt+φ) + sin$^{2}$(ωt+φ) = 1 nên W = ½.mω$^{2}$A$^{2}$

Luyện tập trang 25 sgk vật lý 11 ctst

Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng, hãy chỉ ra những khoảng thời gian trong một chu kì dao động mà:

a) Thế năng tăng dần trong khi động năng giảm dần.

b) Thế năng giảm dần trong khi động năng tăng dần.

Đáp án:     

a) Vật dao động từ vị trí cân bằng về hai biên.

b) Vật dao động từ vị trí biên về vị trí cân bằng.

Vận dụng trang 25 sgk vật lý 11 ctst

Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hoà là x = 5cos(20t) (cm). 

a) Tính cơ năng trong quá trình dao động.

b) Viết biểu thức thế năng và động năng.

Đáp án:     

a) Cơ năng W = ½.mω$^{2}$A$^{2}$ = ½.0,2.20$^{2}$.0,05$^{2}$ = 0,11(J)

b) Thế năng:

$W_{t}$ = ½.mω$^{2}$A$^{2}$cos$^{2}$(ωt+φ0) = ½.0,2.20$^{2}$.0,05$^{2}$cos$^{2}$(20t) = 0,1cos$^{2}$(20t)

Động năng:

$W_{đ}$ = ½.mω$^{2}$A$^{2}$sin$^{2}$(ωt+φ0) = ½.0,2.20$^{2}$.0,05$^{2}$sin$^{2}$(20t) = 0,1sin$^{2}$(20t)

Bài tập 1 trang 25 sgk vật lý 11 ctst

Một hệ dao động điều hoà với chu kì 2 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?

Đáp án:

T=2s => ω = π(rad/s)

$W_{t}$ = $W_{đ}$

⇒ ½.mω$^{2}$A$^{2}$cos$^{2}$(ωt+φ0) = ½.mω$^{2}$A$^{2}$sin$^{2}$(ωt+φ0)

⇒ cos$^{2}$(πt+φ0) = sin$^{2}$(πt+φ0)

⇒ πt + φ0 = π/4+ kπ/2

Lần thứ nhất động năng và thế năng bằng nhau nên k = 1, t = 0 nên ta có: φ0 = 3π/4

Động năng và thế năng bằng nhau lần thứ hai sau khoảng thời gian:

Πt + 3π/4 = π/4 + 2π/2 ⇒ t = 0,5s

Bài tập 2 trang 25 sgk vật lý 11 ctst

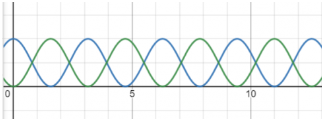
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau.

Đáp án:     

Phương trình dao động: x = Acos(ωt−π/2) 

Thế năng: $W_{t}$ = ½.mω$^{2}$A$^{2}$cos$^{2}$(ωt−π/2)

Động năng: $W_{đ}$= ½.mω$^{2}$A$^{2}$sin$^{2}$(ωt−π/2)

Đường màu xanh lá cây là thế năng, đường màu xanh nước biển là động năng

Trên đồ thị những thời điểm mà hai đồ thị cắt nhau thì động năng và thế năng có độ lớn bằng nhau

T/8 + k.T/4 (k=0;1;2;3;...)