Tải giáo án Powerpoint Toán 7 CTST bài 5: Đường trung trực của một đoạn thẳng

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!

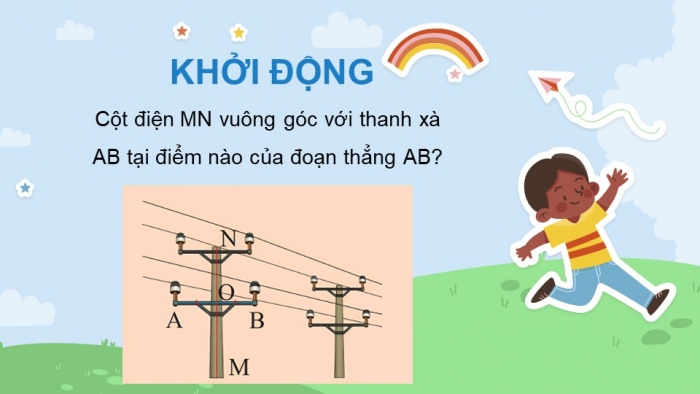
KHỞI ĐỘNG

Cột điện MN vuông góc với thanh xà AB tại điểm nào của đoạn thẳng AB?

BÀI 5: ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG

NỘI DUNG BÀI HỌC

Đường trung trực của một đoạn thẳng

Tính chất của đường trung trực

1. Đường trung trực của một đoạn thẳng

Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng . Sau đó gấp mảnh giấy sao cho điểm  trùng với điểm  (Hình  ).

Theo em nếp gấp xy có vuông góc với đoạn  tại trung điểm hay không? Tại sao?

KẾT LUẬN

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.

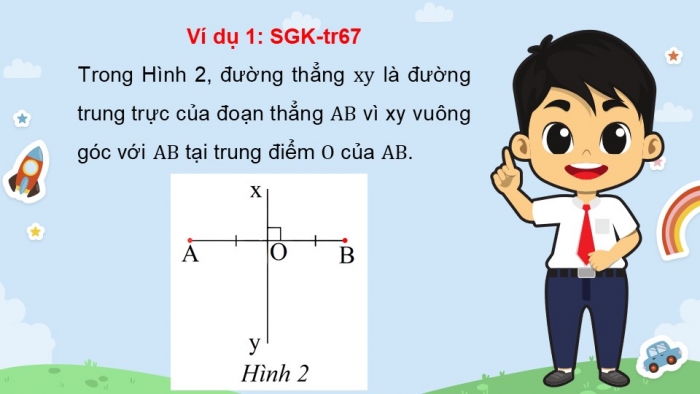
Ví dụ 1: SGK-tr67

Trong Hình 2, đường thẳng  là đường trung trực của đoạn thẳng  vì xy vuông góc với  tại trung điểm  của .

Thực hành 1:

Cho hình chữ nhật , trên cạnh  lấy các điểm  và trên cạnh  lấy các điểm . Cho biết  và ,  đều song song với  (Hình 3 ). Tìm đường trung trực của mỗi đoạn thẳng  và .

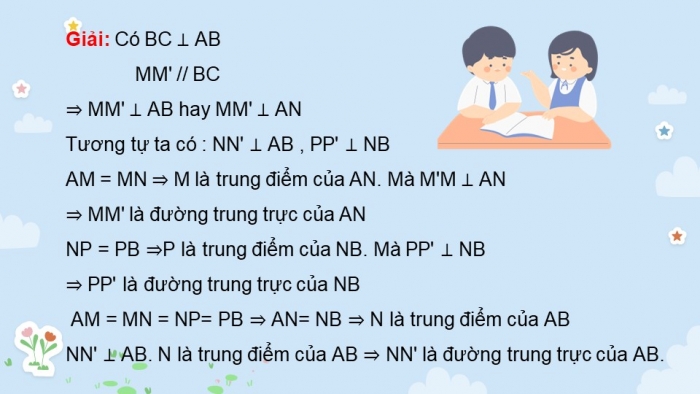
Giải: Có BC ⊥ AB

             MM' // BC  

 MM' ⊥ AB hay MM' ⊥ AN

Tương tự ta có : NN' ⊥ AB , PP' ⊥ NB

AM = MN  M là trung điểm của AN. Mà M'M ⊥ AN

 MM' là đường trung trực của AN

NP = PB P là trung điểm của NB. Mà PP' ⊥ NB

 PP' là đường trung trực của NB

 AM = MN = NP= PB  AN= NB  N là trung điểm của AB

NN' ⊥ AB. N là trung điểm của AB  NN' là đường trung trực của AB.

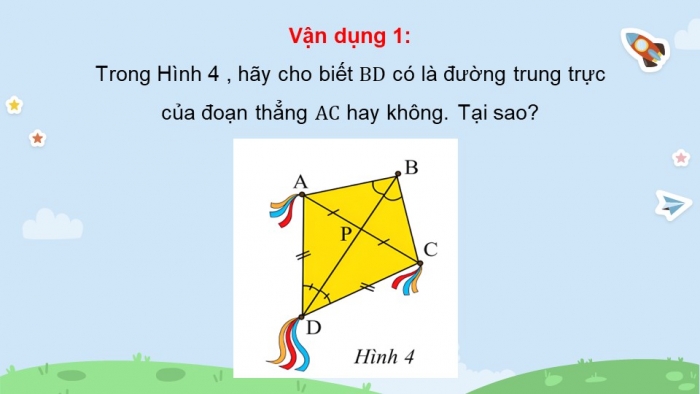
Vận dụng 1:

Trong Hình 4 , hãy cho biết  có là đường trung trực của đoạn thẳng  hay không. Tại sao?

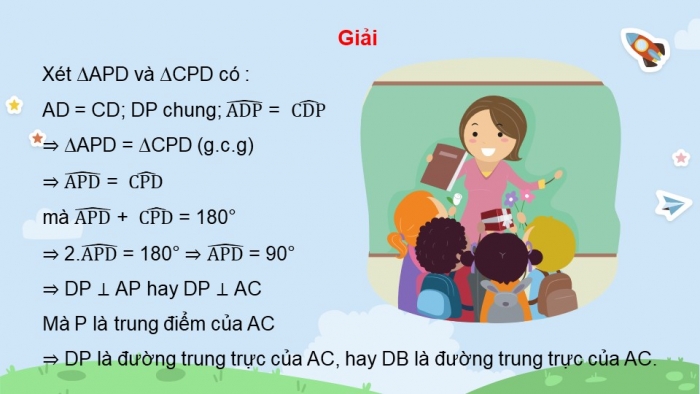
Giải

Xét ∆APD và ∆CPD có :

AD = CD; DP chung;  =  

 ∆APD = ∆CPD (g.c.g)

   =    

mà   +    = 180°

2. = 180°    = 90°

 DP ⊥ AP hay DP ⊥ AC

Mà P là trung điểm của AC

 DP là đường trung trực của AC, hay DB là đường trung trực của AC.

2. Tính chất của đường trung trực

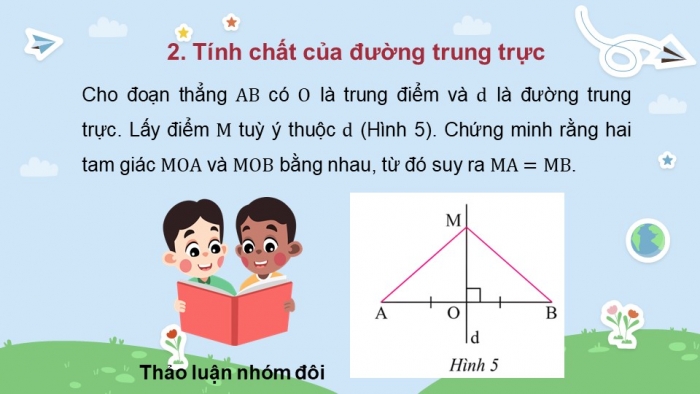
Cho đoạn thẳng  có  là trung điểm và  là đường trung trực. Lấy điểm  tuỳ ý thuộc  (Hình 5). Chứng minh rằng hai tam giác  và  bằng nhau, từ đó suy ra .

Giải

d là đường trung trực của AB tại điểm O

 ∆MOA và ∆MOB là hai tam giác vuông tại O.

Xét ∆MOA và ∆MOB cùng vuông tại đỉnh O ta có:

MO chung

AO = OB ( O là trung điểm của AB)

 ∆MOA = ∆MOB (hai cạnh góc vuông)

 MA = MB.

KẾT LUẬN

Định lí 1:

Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Định lí 2:

Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Thực hành 2:      

Trong Hình 8, cho biết  là đường trung trực của đoạn thẳng , điểm  thuộc đường thẳng  và . Tính .

Giải: M thuộc đường thẳng d mà d là đường trung trực của AB

 MA = MB

 x + 2 = 7 

 x = 7 - 2 = 5.

Vậy x = 5.