Tải giáo án Powerpoint Toán 11 CTST Bài tập cuối chương 7

CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

CHƯƠNG VII. ĐẠO HÀM

BÀI TẬP CUỐI CHƯƠNG VII

BÀI TẬP TRẮC NGHIỆM

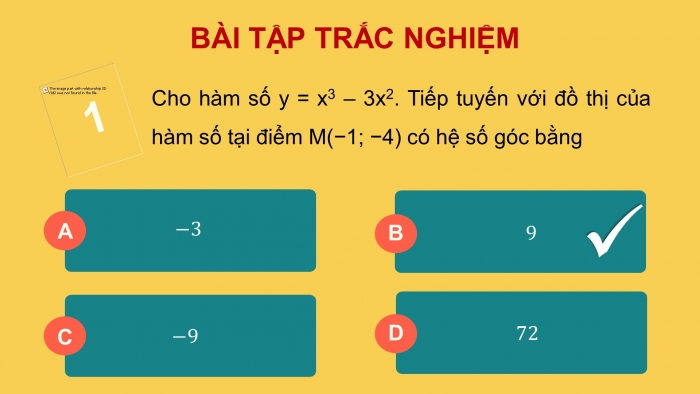
Cho hàm số y = x³ – 3x². Tiếp tuyến với đồ thị của hàm số tại điểm M(−1; −4) có hệ số góc bằng

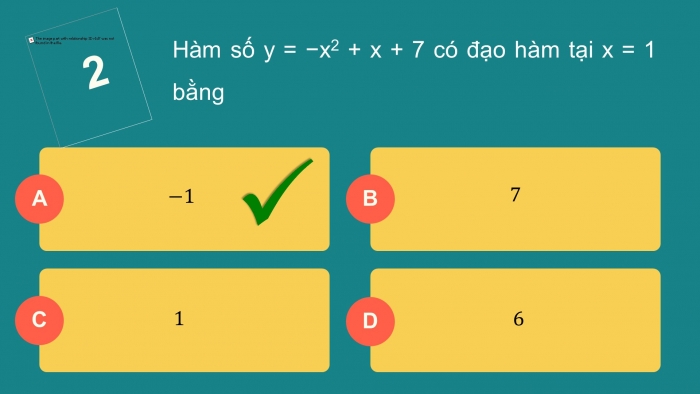
Hàm số y = −x² + x + 7 có đạo hàm tại x = 1 bằng

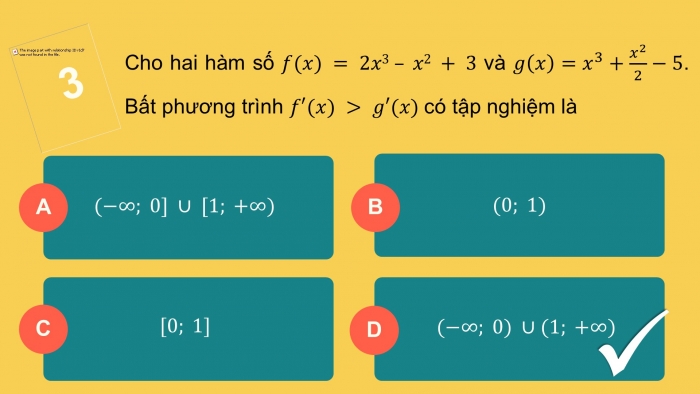
Cho hai hàm số  và . Bất phương trình có tập nghiệm là

Ôn tập kiến thức trọng tâm có trong chương VII

• Trình bày định nghĩa của đạo hàm.
• Trình bày ý nghĩa vật lý của đạo hàm.
• Trình bày công thức viết phương trình tiếp tuyến.
• Trình bày về số e.
• Trình bày bảng đạo hàm của hàm số sơ cấp và hàm hợp.
• Trình bày quy tắc tính đạo hàm của tổng, hiệu, tích, thương.
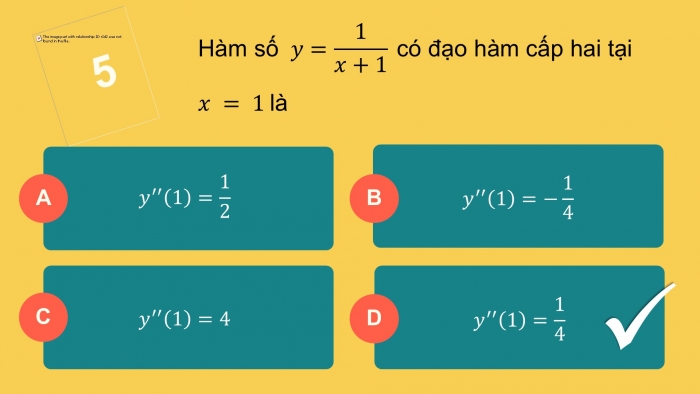
• Trình bày định nghĩa đạo hàm cấp hai.
• Trình bày ý nghĩa cơ học của đạo hàm cấp hai.

• Định nghĩa đạo hàm:

Cho hàm số  xác định trên khoảng  và .

Nếu tồn tại giới hạn hữu hạn

Thì giới hạn này được gọi là đạo hàm của hàm số f(x) tại , kí hiệu là  hoặc .

• Ý nghĩa vật lý của đạo hàm
• Nếu hàm số biểu thị quãng đường di chuyển của vật theo thời gian  thì  biểu thị tốc độ tức thời của chuyển động tại thời điểm .
• Nếu hàm số biểu thị nhiệt độ  theo thời gian  thì  biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm .

• Phương trình tiếp tuyến

Cho hàm số  xác định trên khoảng  và có đạo hàm tại . Gọi  là đồ thị của hàm số đó.

Đạo hàm của hàm số  tại điểm  là hệ số góc của tiếp tuyến  của  tại điểm

Tiếp tuyến   có phương trình là

• Số e

Tổng quát, nếu một năm được chia thành  kì hạn thì

(với

Khi kì hạn càng ngắn thì càng lớn, do đói  càng lớn. Người ta chứng minh được rằng có giới hạn hữu hạn

(với  là số vô tỉ và

Khi kì hạn trở nên rất ngắn (m dần đến ) thì  dần đến , và do đó dần đến .

• Bảng đạo hàm của một số hàm sơ cấp và hàm hợp

• Đạo hàm của tổng, hiệu, tích, thương

Cho hai hàm số  có đạo hàm tại điểm  thuộc tập xác định.

Ta có:

• Đạo hàm cấp hai

Cho hàm số  có đạo hàm  tại mọi .

Nếu hàm số  có đạo hàm tại  thì ta gọi đạo hàm của  là đạo hàm cấp hai của hàm số  tại , kí hiệu  hoặc .

• Ý nghĩa cơ học của đạo hàm cấp hai

Đạo hàm cấp hai  là gia tốc tức thời tại thời điểm  của vật chuyển động có phương trình .

LUYỆN TẬP

Bài 6 (SGK - tr.51) Cho hàm số có đồ thị  và điểm . Viết phương trình tiếp tuyến với  tại điểm .

Giải

Ta có:

Hệ số góc của tiếp tuyến tại  là:

Phương trình tiếp với  tại điểm  là:

Vậy  là tiếp tuyến cần tìm.

Bài 7 (SGK - tr.51) Tính đạo hàm của các hàm số sau: