Tải giáo án Powerpoint Toán 11 CTST Bài 3 Hai mặt phẳng vuông góc

THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI

KHỞI ĐỘNG

Trong thực tế người ta thường nói mặt ngang và mặt đứng của các bậc thang vuông góc với nhau. Vậy thể nào là hai mặt phẳng vuông góc?

BÀI 3: HAI MẶT PHẲNG VUÔNG GÓC

NỘI DUNG BÀI HỌC

Góc giữa hai mặt phẳng

Hai mặt phẳng vuông góc

Tính chất cơ bản về hai mặt phẳng vuông góc

Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

Hình chóp đều. Hình chóp cụt đều

01 GÓC GIỮA HAI MẶT PHẲNG

HĐKP1:

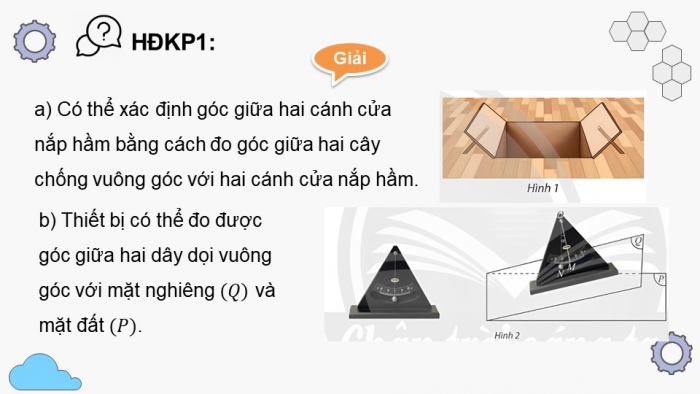
1. a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?
2. b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng (Q) và mặt đất (P).

Giải

1. a) Có thể xác định góc giữa hai cánh cửa nắp hầm bằng cách đo góc giữa hai cây chống vuông góc với hai cánh cửa nắp hầm.
2. b) Thiết bị có thể đo được góc giữa hai dây dọi vuông góc với mặt nghiêng và mặt đất .

ĐỊNH NGHĨA

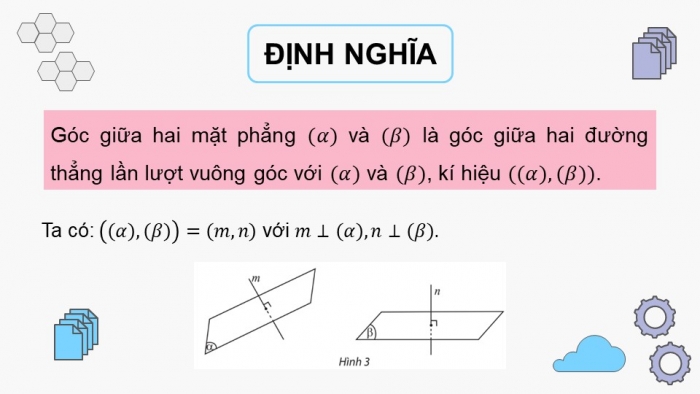
Góc giữa hai mặt phẳng  và  là góc giữa hai đường thẳng lần lượt vuông góc với  và , kí hiệu .

Ta có:  với

NHẬN XÉT

Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.

Cho

với

Ví dụ 1

                                Cho hình chóp có đáy  là hình vuông tâm , cạnh bên  vuông góc với mặt phẳng đáy. Tính góc giữa hai mặt phẳng:

1. a) và ; b) và

Giải

1. a) Ta có: và , suy ra

      và , suy ra .

 Do đó, nếu gọi góc giữa hai mặt phẳng ) và           

      là  thì .

1. b) Ta có: và , suy ra

    và , suy ra

Do đó, nếu gọi góc giữa hai mặt phẳng và

       là  thì .

02 HAI MẶT PHẲNG VUÔNG GÓC

HĐKP2:

Từ một điểm  vẽ hai tia  và  lần lượt vuông góc với hai bức tường trong phòng. Đo góc .

Giải

ĐỊNH NGHĨA

Hai mặt phẳng được gọi là vuông góc nếu góc giữa hai mặt phẳng đó là một góc vuông. Hai mặt phẳng  và  vuông góc được kí hiệu là .

Điều kiện để hai mặt phẳng vuông góc

                   Cho hai mặt phẳng  và cắt nhau theo giao tuyến d điểm  không thuộc và Gọi  và  lần lượt là hình chiếu vuông góc của  lên và Gọi  là giao điểm của  và (Hình 8). 

1. a) Giả sử , hãy cho biết tứ giác là hình gì? Tìm trong đường thẳng vuông góc với .
2. b) Giả sử chứa đường thẳng a với , hãy cho biết tứ giác là hình gì? Tính góc giữa và .

Giải

1. a) Vì nên ; nên 

Mà nên 

Suy ra  là hình chữ nhật.

Trong  có 

1. b) nên nên 

Suy ra .

Mà  nên  là hình chữ nhật

Góc giữa và  là 

Định lí 1

Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Ví dụ 2:

Cho tứ diện  có đôi một vuông góc với nhau. Chứng minh rằng các mặt phẳng , đôi một vuông góc với nhau.

Giải

Ta có

Tương tự ta cũng có .

Vậy các mặt phẳng từng đôi một vuông góc với nhau.

Thực hành 1

Cho hình chóp có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:

1. a)  b) 

Giải

Gọi  là tâm hình vuông.
a) Ta có  và ,

suy ra ,

suy ra .

1. b) Ta có và ,

suy ra ,

suy ra .

Vận dụng 1