Tải giáo án Powerpoint Toán 10 KNTT bài 1: Mệnh đề

CHÀO MỪNG CẢ LỚP ĐẾN VỚI BUỔI HỌC HÔM NAY!

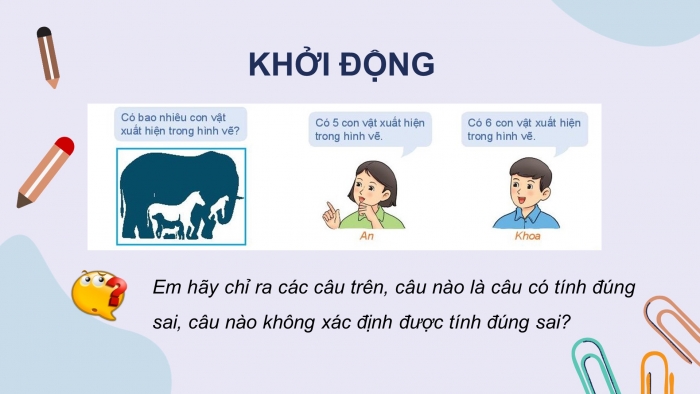
KHỞI ĐỘNG

Em hãy chỉ ra các câu trên, câu nào là câu có tính đúng sai, câu nào không xác định được tính đúng sai?

CHƯƠNG I: MỆNH ĐỀ VÀ TẬP HỢP

BÀI 1: MỆNH ĐỀ

Tiết 1: MỆNH ĐỀ, MỆNH ĐỀ CHỨA BIẾN. MỆNH ĐỀ PHỦ ĐỊNH

1. Mệnh đề, mệnh đề chứa biến
2. Mệnh đề

Trong các câu ở tình huống mở đầu:

1. Câu nào đúng?
2. Câu nào sai?
3. Câu nào không xác định được tính đúng sai?
4. a) Câu đúng: “Có 6 con vật xuất hiện trong hình vẽ”.
5. b) Câu sai: “Có 5 con vật xuất hiện trong hình vẽ”.
6. c) Câu không xác định tính đúng sai: “Có bao nhiêu con vật xuất hiện trong hình vẽ?”.

Những câu không xác định được tính đúng sai không phải là mệnh đề.

KẾT LUẬN

• Mỗi mệnh đề phải hoặc đúng hoặc sai.
• Mỗi mệnh đề không thể vừa đúng vừa sai.

Chú ý

Người ta thường sử dụng các chữ cái P, Q, R, ... để biểu thị các mệnh đề.

Ví dụ 1

Trong các câu sau, câu nào là mệnh đề? Câu nào không là mệnh đề?

1. Phương trình 3x² - 5x + 2 = 0 có nghiệm nguyên;
2. 5 < 7 - 3
3. Có bao nhiêu dấu hiệu nhận biết hai tam giác đồng dạng?
4. Đấy là cách xử lí khôn ngoan!

Giải

Câu c là câu hỏi; câu d là câu cảm thán, nêu lên ý kiến của người nói. Do đó, không xác định được tính đúng sai. Vậy các câu c và d không phải là mệnh đề.

Những câu nghi vấn, câu cảm thán, câu cầu khiến không phải là mệnh đề.

Những mệnh đề liênq quan đến toán học được gọi là mệnh đề toán học.

Ví dụ: Phương trình x² + 2x  + 1 = 0 có nghiệm nguyên.

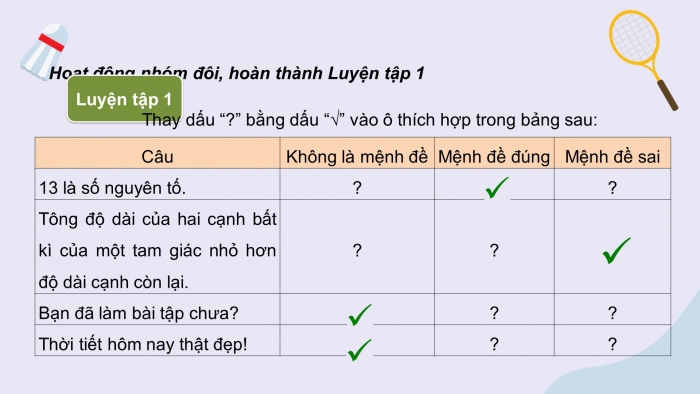
Hoạt động nhóm đôi, hoàn thành Luyện tập 1

Luyện tập 1

Thay dấu “?” bằng dấu “√” vào ô thích hợp trong bảng sau:

1. Mệnh đề chứa biến

Xét câu “n chia hết cho 2” (với n là số tự nhiên).

Ta chưa khẳng định được tính đúng sai, tuy nhiên với mỗi giá trị của n thuộc tập số tự nhiên ta lại thu được một mệnh đề đúng hoặc sai. Chẳng hạn:

• Với n = 5 ta được mệnh đề “5 chia hết cho 2”.
• Mệnh đề sai

Với n = 10 ta được mệnh đề “10 chia hết cho 2”.

• Mệnh đề đúng

“n chia hết cho 2” là một mệnh đề chứa biến.

Mệnh đề chứa biến là một câu chứa biến, với mỗi giá trị của biến thuộc một tập nào đó, ta được một mệnh đề.

Ví dụ

               P: “2 + n = 5”

Q: “x > 3”

M: “x + y  < 2”

Xét câu “x > 5”. Hãy tìm hai giá trị thực của x để từ câu đã cho, ta nhận được một mệnh đề đúng và một mệnh đề sai.

Gợi ý

• Với x = 8, "8 > 5" là mệnh đề đúng.
• Với x = 3, "3 > 5" là mệnh đề sai.

2. Mệnh đề phủ định

  Quan sát biển báo trong hình bên.

Khoa nói: “Đây là biển báo đường dành cho người đi bộ”.

An không đồng ý với ý kiến của Khoa. Hãy phát biểu ý kiến của Khoa dưới dạng một mệnh đề.

Để phủ định mệnh đề P, người ta thường thêm hoặc bớt từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P, kí hiệu  là mệnh đề phủ định của P.

Kết luận:

Mệnh đề P và mệnh đề  là hai phát biểu trái ngược nhau. Nếu P đúng thì  sai, còn nếu P sai thì  đúng.

Ví dụ 2

Phát biểu mệnh đề phủ định của mỗi mệnh đề sau:

P: “17 là số chính phương”;

Q: “Hình hộp chữ nhật không phải là hình lăng trụ đứng tứ giác”.

Giải

Mệnh đề phủ định của P là : “17 không phải là số chính phương”.

Mệnh đề phủ định của Q là : “Hình hộp chữ nhật là hình lăng trụ đứng tứ giác”.

Luyện tập 2

Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó.

P: “ 2 022 chia hết cho 5”;

Q: “Bất phương trình 2x + 1 > 0 có nghiệm”.

Giải

: “2022 không chia hết cho 5”, là mệnh đề đúng.

: “Bất phương trình 2x + 1 > 0 không có nghiệm”, mệnh đề sai.