Tải giáo án Powerpoint Toán 10 KNTT bài 25: Nhị thức newton

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MỚI!
KHỞI  ĐỘNG

Cho các khai triển

Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển  khi  không?

BÀI 25:
NHỊ THỨC NEWTON

NỘI DUNG BÀI HỌC
Khai triển lũy thừa của nhị thức bằng sơ đồ cây

Vận dụng công thức nhị thức

Thảo luận nhóm: hãy đọc nội dung HĐ1 và trả lời câu hỏi.

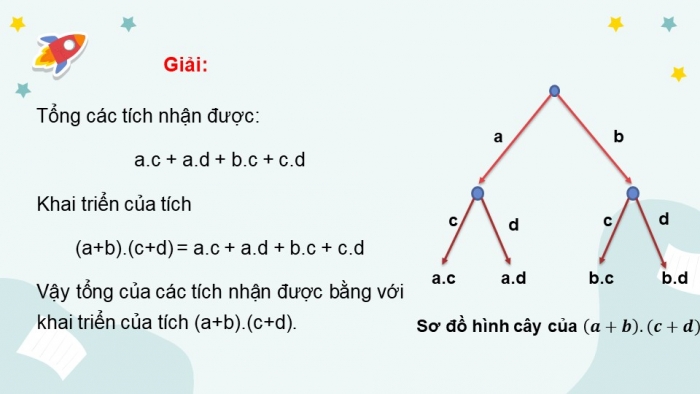
                      Sơ đồ hình cây của tích hai nhị thức (a + b).(c + d) được xây dựng như sau:

• Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);
• Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;
• Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.

Giải:

Tổng các tích nhận được:

a.c + a.d + b.c + c.d

Khai triển của tích

(a+b).(c+d) = a.c + a.d + b.c + c.d

Vậy tổng của các tích nhận được bằng với khai triển của tích (a+b).(c+d).

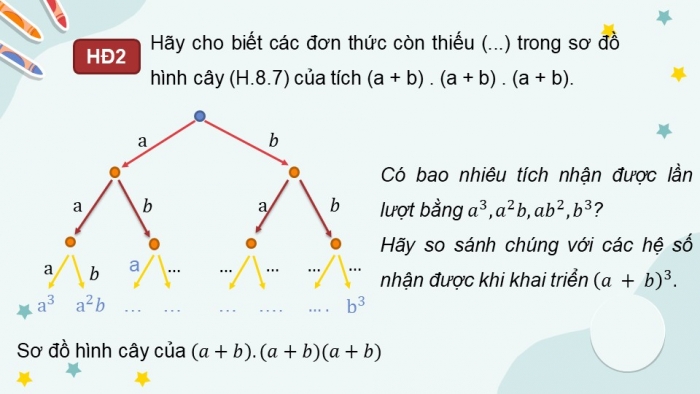
Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b). 

Có bao nhiêu tích nhận được lần lượt bằng ?

Hãy so sánh chúng với các hệ số nhận được khi khai triển

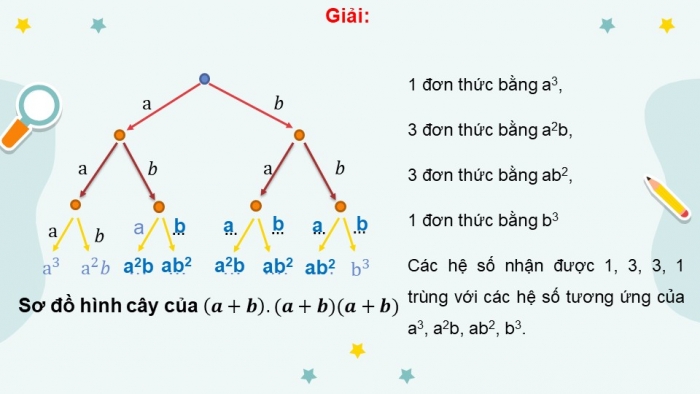
Giải:

1 đơn thức bằng a³,

3 đơn thức bằng a²b,

3 đơn thức bằng ab²,

1 đơn thức bằng b³

Các hệ số nhận được 1, 3, 3, 1 trùng với các hệ số tương ứng của a³, a²b, ab², b³.

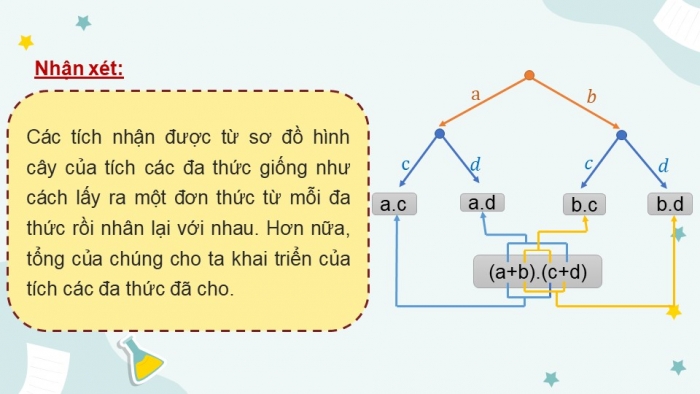
Nhận xét:

Các tích nhận được từ sơ đồ hình cây của tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Hơn nữa, tổng của chúng cho ta khai triển của tích các đa thức đã cho.

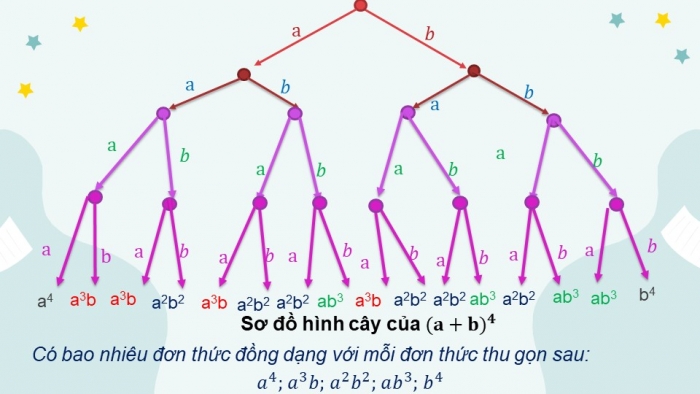
HĐ3

Sơ đồ hình cây của khai triển được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm  (theo quy tắc nhân) đơn thức có dạng x . y . z . t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a . a . b . a, thu gọn là . Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với   trong tổng là  .

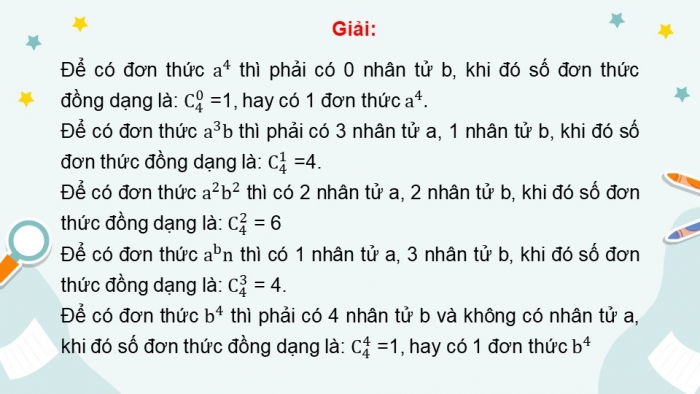
Giải:

Để có đơn thức  thì phải có 0 nhân tử b, khi đó số đơn thức đồng dạng là:  =1, hay có 1 đơn thức

Để có đơn thức  thì phải có 3 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng là:  =4.

Để có đơn thức  thì có 2 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng là:  = 6

Để có đơn thức  thì có 1 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng là:  = 4.

Để có đơn thức  thì phải có 4 nhân tử b và không có nhân tử a, khi đó số đơn thức đồng dạng là:  =1, hay có 1 đơn thức