Tải giáo án Powerpoint Toán 10 KNTT bài 24: Hoán vị, chỉnh hợp và tổ hợp

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!

KHỞI ĐỘNG

Danh sách các cầu thủ của Đội tuyển bóng đá quốc gia tham dự một trận đấu quốc tế có 23 cầu thủ gồm 3 thủ môn, 7 hậu vệ, 8 tiền vệ và 5 tiền đạo. Huấn luyện viên rất bí mật, không cho ai biết đội hình (danh sách 11 cầu thủ) sẽ ra sân.

Trong cuộc họp báo, ông chỉ tiết lộ đội sẽ đá theo sơ đồ 3 - 4 - 3 (nghĩa là 3 hậu vệ, 4 tiền vệ. 3 tiền đạo và 1 thủ môn). Đối thủ đã có danh sách 23 cầu thủ (tên và vị trí của từng cầu thủ) và rất muốn dự đoán đội hình, họ xét hết các khả năng có thể xảy ra.

Hỏi nếu đối thủ đã dự đoán được trước vị trí thủ môn thì họ sẽ phải xét bao nhiêu đội hình có thể?

BÀI 24

HOÁN VỊ, CHỈNH HỢP VÀ TỔ HỢP

NỘI DUNG BÀI HỌC

Hoán vị

Chỉnh hợp

Tổ hợp

Ứng dụng hoán vị, chỉnh hợp, tổ hợp vào các bài toán đếm

Sử dụng máy tính cầm tay

HOÁN VỊ

Hoạt động 1

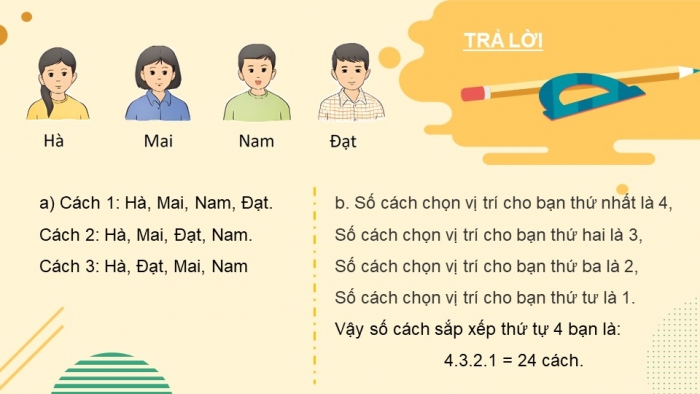
Một nhóm gồm bốn bạn Hà, Mai, Nam, Đạt xếp thành một hàng, từ trái sang phải, để tham gia một cuộc phỏng vấn.

1. a) Hãy liệt kê ba cách sắp xếp bốn bạn trên theo thứ tự.
2. b) Có bao nhiêu cách sắp xếp thứ tự bốn bạn trên để tham gia phỏng vấn?
3. a) Cách 1: Hà, Mai, Nam, Đạt.

Cách 2: Hà, Mai, Đạt, Nam.

Cách 3: Hà, Đạt, Mai, Nam

TRẢ LỜI

1. Số cách chọn vị trí cho bạn thứ nhất là 4,

Số cách chọn vị trí cho bạn thứ hai là 3, 

Số cách chọn vị trí cho bạn thứ ba là 2,

Số cách chọn vị trí cho bạn thứ tư là 1.

Vậy số cách sắp xếp thứ tự 4 bạn là:

4.3.2.1 = 24 cách.

KẾT LUẬN

• Một hoán vị của một tập hợp có n phần tử là một cách sắp xếp có thứ tự n phần tử đó (với n là một số tự nhiên, ).
• Số các hoán vị của tập hợp có n phần tử, kí hiệu là P_n được tính bằng công thức:

Chú ý:

Quy ước: 0! = 1.

Ví dụ 1 (SGK - tr 67)

Từ các chữ số  và 9 có thể lập được bao nhiêu số có bốn chữ số khác nhau?

Giải

Mỗi cách sắp xếp bốn chữ số đã cho để lập thành một số có bốn chữ số khác nhau là một hoán vị của bốn chữ số đó.

Vậy số các số có bốn chữ số khác nhau có thể lập được là

.

Luyện tập 1

Trong một cuộc thi điền kinh gồm 6 vận động viên chạy trên 6 đường chạy. Hỏi có bao nhiêu cách sắp xếp các vận động viên vào các đường chạy đó?

Giải

Số cách xếp các vận động viên vào các đường chạy là một hoán vị của 6 phần tử.

Vậy số cách sắp xếp là  cách.