Tải giáo án Powerpoint Toán 10 KNTT bài 6: Hệ thức lượng trong tam giác (4 tiết)

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Ngắm Tháp Rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?

BÀI 6: HỆ THỨC LƯỢNG TRONG TAM GIÁC (4 Tiết)

NỘI DUNG BÀI HỌC

Định lí côsin

Định lí sin

Giải tam giác và ứng dụng thực tế

Công thức tính diện tích tam giác

1. Định lí côsin

                Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20 km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc và đi tiếp.

1. Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1 km trên thực tế ứng với 1 cm trên bản vẽ).
2. Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilomet (số đo gần đúng).
3. Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hương đông nam) thì có thể dụng Định lí Pythagore (Pi-ta-go) để tính chính xác các số đo trong câu b hay không?

Giải

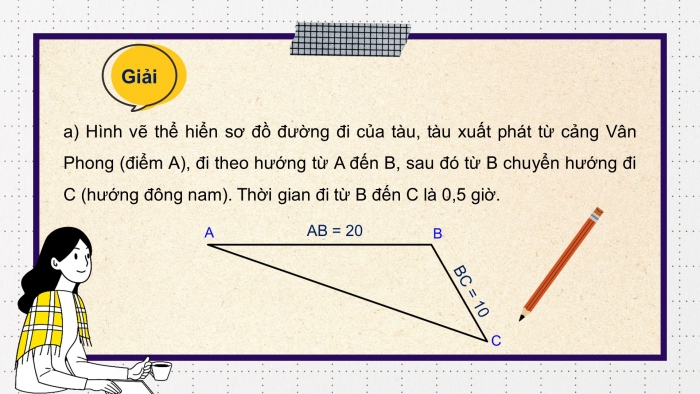
1. a) Hình vẽ thể hiển sơ đồ đường đi của tàu, tàu xuất phát từ cảng Vân Phong (điểm A), đi theo hướng từ A đến B, sau đó từ B chuyển hướng đi C (hướng đông nam). Thời gian đi từ B đến C là 0,5 giờ.
2. b) Khoảng cách từ C đến A khoảng 28 cm, thì thực tế tàu cách cảng Vân Phong 28 km.
3. c) Có thể dùng Định lí Pythagore (Pi-ta-go) vì nếu tàu chuyển hướng sang nam thì góc ABC là góc vuông, ta có thể áp dụng định lí Pythagore (Pi-ta-go).

Có hay không, một kiểu định lí Pythagore cho tam giác tùy ý?

Ghi nhớ

• Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng;
• a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C;
• p là nửa chu vi;
• S là diện tích;
• R, r tương ứng là bán kính đường tròn ngoại tiếp và nội tiếp tam giác.

Thảo luận nhóm đôi, hoàn thành HĐ2.

HĐ2

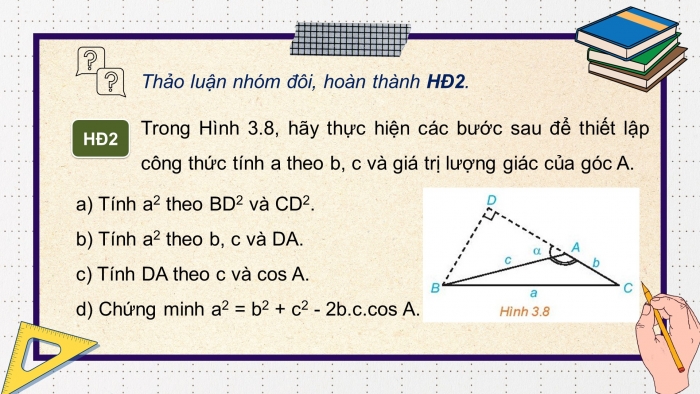
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.

2. a) Tính a² theo BD² và CD².
3. b) Tính a² theo b, c và DA.
4. c) Tính DA theo c và cos A.
5. d) Chứng minh a² = b² + c² - c.cos A.

Giải

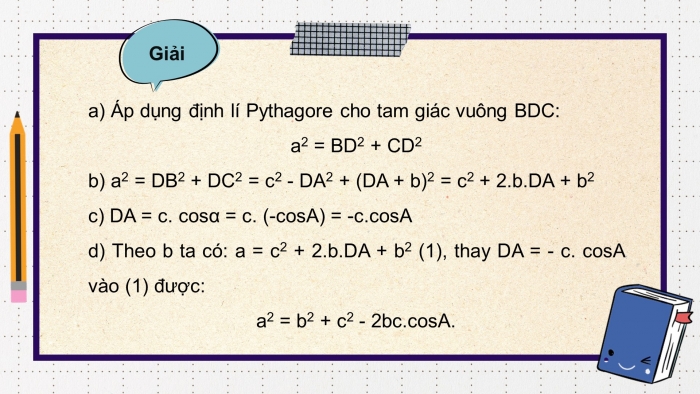
1. a) Áp dụng định lí Pythagore cho tam giác vuông BDC:

a² = BD² + CD²

2. b) a² = DB² + DC² = c² - DA² + (DA + b)² = c² + b.DA + b²
3. c) DA = cos⁡α = c. (-cosA) = -c.cosA
4. d) Theo b ta có: a = c² + b.DA + b² (1), thay DA = - c. cosA vào (1) được:

a² = b² + c² - 2bc.cos⁡A.

    Kết quả câu d còn đúng không khi góc A là góc vuông?

Còn đúng, vì khi A vuông thì cos⁡A = 0, a² = b² + c²

Em hãy nhận xét mối quan hệ giữa độ dài cạnh BC với độ dài các cạnh BA, AC và côsin của góc A.

Định lí côsin

Trong tam giác ABC:

a² = b² + c² - 2bc.cos⁡A

b² = c² + a² - 2ca.cos⁡B

c² = a² + b² - 2ab.cos⁡C

Định lí Pythagore có phải là một trường hợp đặc biệt của định lí Cosin hay không?

Định lí Pythagore là một trường hợp đặc biệt của định lí Côsin, khi góc A = 90^o.

Đọc Ví dụ 1 và cho biết: Tam giác ABC đã biết các yếu tố nào? Để tính được BC ta dùng định lí côsin như thế nào?

Ví dụ 1

Cho tam giác ABC có  = 120^o và AB = 5, AC = 8. Tính độ dài cạnh BC.

Giải

Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² - 2AB. AC. cos120^o

        = 5² + 8² - 2.5.8.  = 129.

Vậy BC = 

Khám phá

Từ định lí cosin, hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.