Giải SBT toán 8 chân trời tập 2 bài Bài tập cuối chương 7

A. CÂU HỎI TRẮC NGHIỆM

Câu 1 trang 48 SBT Toán 8 tập 2 CTST: Cho hai đoạn thẳng AB=12 am, CD = 10 cm. Tỉ số của hai đoạn thẳng AB và CD là

A.$\frac{AB}{CD} = \frac{5}{6}$

B.$\frac{AB}{CD} = \frac{6}{5}$

C.$\frac{AB}{CD} = \frac{4}{3}$

D.$\frac{AB}{CD} = \frac{3}{4}$

Hướng dẫn trả lời:

Đáp án đúng B.$\frac{AB}{CD} = \frac{6}{5}$

$\frac{AB}{CD} =\frac{12}{10}= \frac{6}{5}$

Câu 2 trang 48 SBT Toán 8 tập 2 CTST: Quan sát Hinh 1. Biết MN = 1 cm, MM' // NN’, OM'=3 cm, M'N'= 1,5 cm, độ dài đoạn thẳng OM trong Hình 1 là 

A. 3 cm.

B. 1,5 cm.

C. 2 cm.

D. 2,5 cm.

Hướng dẫn trả lời:

Đáp án đúng C. 2 cm.

Ta có $\frac{OM}{MN} = \frac{OM’}{M’N’} = \frac{OM}{1} = \frac{3}{1,5}$

$\Rightarrow OM=  2cm$

Câu 3 trang 49 SBT Toán 8 tập 2 CTST: Trong Hình 2 có $\widehat M_{1}= \widehat M_{2}$ .Đẳng thức nào sau đây đúng?

A.$\frac{MN}{MK} = \frac{NK}{KP}$

B.$\frac{MN}{KP} = \frac{MP}{NP}$

C.$\frac{MK}{MP} = \frac{NK}{KP}$

D.$\frac{MN}{NK} = \frac{MP}{KP}$

Hướng dẫn trả lời:

Đáp án đúng D.$\frac{MN}{NK} = \frac{MP}{KP}$

Câu 4 trang 49 SBT Toán 8 tập 2 CTST: Cho tam giác MNP có M'N' // MN (Hình 3). Đẳng thức nào sau đây sai?

A.$\frac{PM’}{PM} = \frac{PN}{PN’}$

B.$\frac{PM’}{PM} = \frac{PN’}{PN}$

C.$\frac{PM’}{M’M} = \frac{PN’}{N’N}$

D.$\frac{M’M}{PM} = \frac{N’N}{PN}$

Hướng dẫn trả lời:

Đáp án đúng C.$\frac{PM’}{M’M} = \frac{PN’}{N’N}$

Câu 5 trang 49 SBT Toán 8 tập 2 CTST: Độ dài x trong Hình 4 là

A. 2,5. 

B. 2,9.

C. 3.

D. 3,2.

Hướng dẫn trả lời:

Đáp án đúng C. 3.

$\frac{3}{3,6} = \frac{2,5}{x} \Rightarrow x = 3 $

Câu 6 trang 49 SBT Toán 8 tập 2 CTST: Trong Hình 5 có MQ là tia phân giác của $\widehat{NMP}$ . Tỉ số $\frac{x}{y}$ là

A. $\frac{5}{2}$

B. $\frac{5}{4}$

C. $\frac{4}{5}$

D. $\frac{2}{5}$

Hướng dẫn trả lời:

Đáp án đúng B. $\frac{5}{4}$

Theo tính chất tia phân giác ta có

$\frac{MP}{MN} =\frac{QP}{NQ}=\frac{2,5}{2} =\frac{5}{4}$

Câu 7 trang 49 SBT Toán 8 tập 2 CTST: Cho hình vuông ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (Hình 6). Đẳng thức nào sau đây đúng?

A.$S_{MNPQ} =\frac{1}{4}S_{ABCD}$

B.$S_{MNPQ} =\frac{1}{3}S_{ABCD}$

C.$S_{MNPQ} =S_{ABCD}$

D.$S_{MNPQ} =\frac{1}{2}S_{ABCD}$

Hướng dẫn trả lời:

Đáp án đúng 

D.$S_{MNPQ} =\frac{1}{2}S_{ABCD}$

Ta có $S_{QAM} = S_{MNB}=S_{CPN}=S_{DPQ} = \frac{QQ.DP}{2} = \frac{a^{2}}{8}$ Lại có $S_{ABCD} = a^{2}$

Nên $S_{MNPQ}= S_{ABCD} -S_{AMQ}-S_{MBN}-S_{CPN} - S_{DPQ}$

=$a^{2} - 4\frac{a^{2}}{8} =\frac{1}{2} .S_{ABCD}$

Vậy $S_{MNPQ} = \frac{1}{2}S_{ABCD}$

Câu 8 trang 50 SBT Toán 8 tập 2 CTST: Cho hình bình hành ABCD có M, N lần lượt là trung điểm của BC, AD. Vẽ MP // BD (P = AC) và NQ//BD($P \in AC$). Phát biểu nào sau đây đúng?

A. AQ=QP=PC.

B. O là trung điểm PQ

C. MNPQ là hình bình hành.

D. MPNQ là hình chữ nhật.

Hướng dẫn trả lời:

Đáp án đúng B. O là trung điểm PQ

O là trung điểm chung của AC và BD

Xét tứ giác AMCN có 

AM//CN

AM=CN

Do đó; AMCN là hình bình hành

Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường

hay O là trung điểm của MN

Ta có: OP+PC=OC

OQ+QA=OA

mà OA=OC

và PC=QA

nên OP=OQ

=>O là trung điểm của PQ

Câu 9 trang 50 SBT Toán 8 tập 2 CTST: Cho tam giác ABC đều cạnh bằng 1 dm. Gọi E, F lần lượt là trung điểm của AB, AC. Chu vi của hình thang EFCB bằng:

A.$\frac{5}{2}$ dm

B.3 dm

C.3,5 dm

B.4 dm

Hướng dẫn trả lời:

Đáp án đúng A.$\frac{5}{2}$ dm

Tam giác ABC dều nên AB = BC = CA 1 dm

Vì E, F lần lượt là trung điểm của AB, AC nên BE = $\frac{1}{2} BC = 0,5 dm

Tam giác ABC có E, F lần lượt là trung điểm của AB, AC nên theo hệ quả định lí Thalès ta có:

EF =$ \frac{1}{2}$ BC = 0,5 dm $

Vậy chu vi hình thang EFCB là:

BE + FE + FC + BC = 1 + 0,5 + 0,5 + 0,5 = 2,5 m

Câu 10 trang 50 SBT Toán 8 tập 2 CTST: Cho hình thang ABCD (AB // CD) và DE=EC (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng? 

(I) $\frac{AK}{EC} = \frac{ KB}{DE}$

(II) AK = KB.

(III) $\frac{AO}{AC} = \frac{AB}{DC}$

(IV) $\frac{AK}{EC} = \frac{OB}{OD}$

A. 1. 

B. 2.

C. 3.

D. 4.

Hướng dẫn trả lời:

Đáp án đúng C. 3.

Tam giác AKO có AK//CE nên theo hệ quả định lí Thalès ta có:

$\frac{AK}{CE} = \frac{KO}{EO} =\frac{AO}{OC}$

Tam giác BKO có BK//DE nên theo hệ quả định lí Thalès ta có:

$\frac{BK}{DE} = \frac{KO}{EO} = \frac{OB}{OD}$

Do đó, $\frac{AK}{DE} = \frac{KO}{EO} =\frac{OB}{OD}$

Mà DE =EC nên AK = KB

Ta có $\frac{AO}{OC} = \frac{AK}{CE} = \frac{2AK}{2CE} = \frac{AB}{DC}$

B.BÀI TẬP TỰ LUẬN

Bài 11 trang 50 SBT Toán 8 tập 2 CTST: Cho tam giác ABC có cạnh BC=10 cm. Trên cạnh AB lấy các điểm D, E sao cho AD =DE=EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC lần lượt tại M và N. Tính độ dài DM và EN.

Hướng dẫn trả lời:

Xét $\Delta$ ABC có DM // BC, theo hệ quả của định lí thales

$\frac{DM}{BC} =\frac{AD}{AB}$, suy ra $\frac{DM}{10}=\frac{1}{3}$

Vậy DM = $\frac{10}{3}$ cm 

Xét $\Delta$ ABC có EN // BC, theo hệ quả của định lí thales

$\frac{EN}{BC} =\frac{AE}{AB}$, suy ra $\frac{EN}{10}=\frac{2}{3}$

Vậy EN = $\frac{10}{3}$ cm 

Bài 12 trang 50 SBT Toán 8 tập 2 CTST: Cho tam giác ABC có I $\in$ AB và K = AC. Kẻ IM // BK (M $\in$ AC), KN // CI (N $\in$ AB). Chứng minh MN // BC.

Hướng dẫn trả lời:

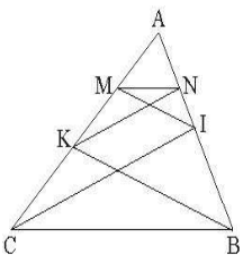
Xét $\Delta$ ABK có IM // BK, theo hệ quả của định lí Thales ta có:

$\frac{DM}{BC} =\frac{AD}{AB}$

Xét $\Delta$ AIC có KN // CI, theo hệ quả của định lí Thales ta có:

$\frac{AN}{AI} =\frac{AK}{AC}$

Do đó $\frac{AI}{AB} .\frac{AN}{AI}=\frac{AM}{AK} .\frac{AK}{AC}$ 

Suy ra $\frac{AN}{AB} =\frac{AM}{AC}$

Xét $\Delta$ ABC có $\frac{AN}{AB} =\frac{AM}{AC}$ nên theo định lí thales đảo ta có MN // BC 

Bài 13 trang 50 SBT Toán 8 tập 2 CTST: Để đo khoảng cách giữa hai điểm A và B bị ngăn cách bởi một hồ nước, người ta đóng các cọc tại các vị trí A, B, M, N, O như Hình 9 và đo được MN=45 m.Tính khoảng cách AB biết M,N lần lượt là trung điểm OA, OB.

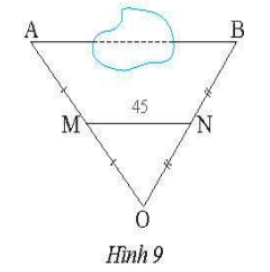
Hướng dẫn trả lời:

Xét tam giác AOB ta có:

M là trung điểm của AO

N là trung điểm của BO

$\Rightarrow$ MN là đường trung bình của tam giác AOB

$\Rightarrow MN =\frac{1}{2} AB$

$\Rightarrow AB = 2MN = 2.45 = 90 (m)$

Bài 14 trang 51 SBT Toán 8 tập 2 CTST: Cho Hình 10, tính độ dài x, y. 

Hướng dẫn trả lời:

Ta có :  EF // DC =>  EFDC là hình thang.

Mặt khác BF = FH = HC; GH vuông góc với ED nên GH là đường trung bình của hình thang EFDC

$\Rightarrow y= GH = \frac{EF+DC}{2} = \frac{10+14}{2} = 12 cm$

Tương tự ta có  AB // GH => ABGH là hình thang.

Mặt khác BF = FH = HC; EF vuông góc với AG nên EF là đường trung bình của hình thang  ABGH

$\Rightarrow  EF = \frac{AB+GH}{2} = \frac{x+12}{2} = 10 \Rightarrow x =8 cm$

Bài 15 trang 51 SBT Toán 8 tập 2 CTST: Cho tam giác ABC vuông tại A có AB=6 cm, AC=8 cm. Tia phân giác của $\widehat{ABC}$ cắt AC tại D.

a) Tính độ dài DA, DC.

b) Tia phân giác của $\widehat{ACB}$ cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh$\widehat{ BIM} =90^{\circ}$.

Hướng dẫn trả lời:

a) Xét tam giác ABC vuông tại A  theo pytago ta có 

$BC = \sqrt{AB^{2}+ AC^{2}} = 10$ cm 

Ta có BD là đường phân giác của $\widehat{ABC}$ trong $\Delta {ABC}$ nên

$\frac{DA}{DC} = \frac{BA}{BC} =\frac{6}{10}=\frac{3}{5}$

$\Rightarrow \frac{DA}{3} =\frac{DC}{5}=\frac{AC}{8}=1$

Vậy DA = 3 cm 

DC = 5 cm

b) Xét tam giác ABD vuông tại A  theo pytago ta có

$BD = \sqrt{AB^{2}+ AD^{2}} = 3\sqrt{5}$ cm 

Ta có CI là đường phân giác của $\widehat{DCB}$ trong $\Delta {BCDC}$ nên

$\frac{ID}{IB} = \frac{CD}{CB} =\frac{5}{10}=\frac{1}{2}$

$\Rightarrow \frac{ID}{1} =\frac{IB}{2}=\frac{BD}{3}=\sqrt{5}$

Vậy ID =  $\sqrt{5}$ cm

IB =$2\sqrt{ 5}$ cm

Ta có $\Delta$ IDC $\Delta$ IMC 

Suy ra $IM=ID = \sqrt{5}$ cm

Ta có $IM^{2} + IB^{2} = 25 = MB^{2}$. 

Áp dụng định lí Pythagore đảo trong $\Delta$ IMB,

suy ra$\widehat{ BIM} =90°$.