Tải giáo án Powerpoint Toán 10 CTST bài 1: Giá trị lượng giác của một góc từ 0° đến 180°

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY
KHỞI ĐỘNG
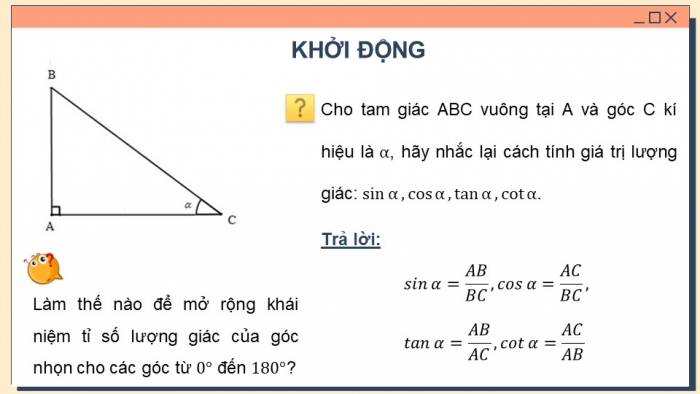
Cho tam giác ABC vuông tại A và góc C kí hiệu là α, hãy nhắc lại cách tính giá trị lượng giác: sin⁡α,cos⁡α,tan⁡α,cot⁡α.
Trả lời:
Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?
sin⁡α=AB/BC,cos⁡α=AC/BC,tan⁡α=AB/AC,cot⁡α=AC/AB
CHƯƠNG IV:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
BÀI 1: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°
NỘI DUNG
Giá trị lượng giác
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Giá trị lượng giác của một số góc đặc biệt
Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
Giá trị lượng giác
HĐKP 1:
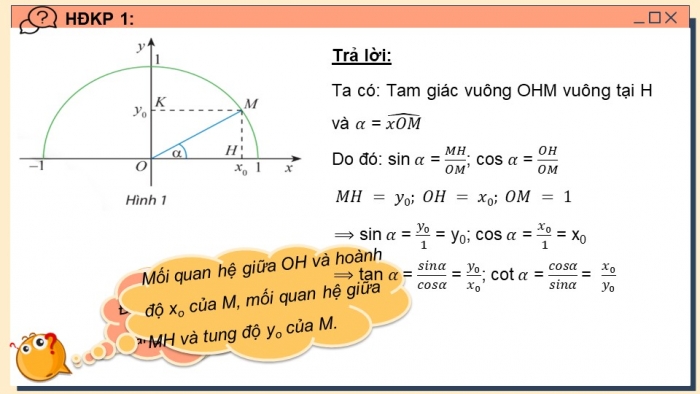
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho (xOM) ̂=α. Giả sử điểm M có tọa độ (x0; y0). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
sinα = y0; cosα =x0 ; tanα = y0/x0; cotα = y0/x0
Trả lời:
Ta có: Tam giác vuông OHM vuông tại H và α = (xOM) ̂
Do đó: sin α = MH/OM; cos α = OH/OM
MH = y0; OH = x0; OM = 1
⟹ sin α = y_0/1 = y0; cos α = x_0/1 = x0
⟹ tan α = sinα/cosα = y_0/x_0 ; cot α = cosα/sinα = x_0/y_0
ĐỊNH NGHĨA
Với mỗi góc α ( 0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho (xOM) ̂ = α. Gọi (x0; y0) là tọa độ điểm M, ta có:
- Tung độ y0 của M là sin của góc α, kí hiệu là sin α = y0.
- Hoành độ x0 của M là côsin của góc α, kí hiệu là cos α = x0;
- Tỉ số y_0/x_0 (x0 ≠ 0) là tang của góc α, kí hiệu là tan α = y_0/x_0 ;
- Tỉ số x_0/y_0 (y0 ≠ 0) là cô tang của góc α, kí hiệu là cotα = x_0/y_0 .
+ Mối quan hệ giữa tan⁡α và sin⁡α,cos⁡α? Tương tự với cot⁡α.
+ Mối quan hệ giữa tan⁡α và cot⁡α.
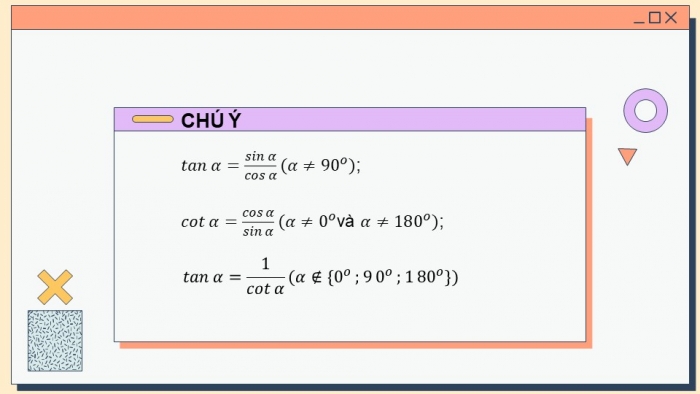
tan⁡α=sin⁡α/cos⁡α (α≠90^o);
cot⁡α=cos⁡α/sin⁡α (α≠0^ovà α≠180^o);
tan⁡α=1/cot⁡α (α∉{0^o ;⁡9 0^o ;⁡1 80^o})
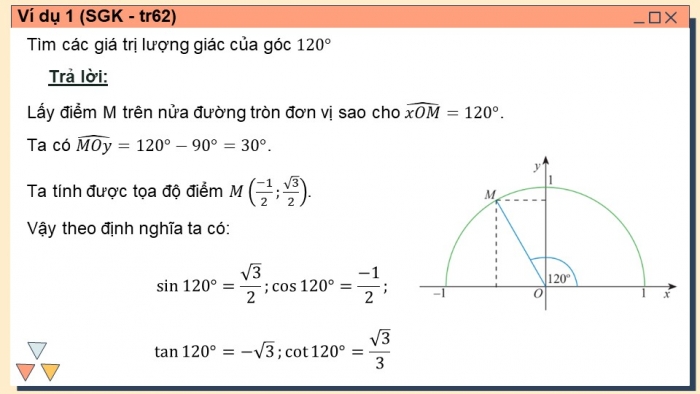
Ví dụ 1 (SGK - tr62)
Tìm các giá trị lượng giác của góc 120°
Trả lời:
Lấy điểm M trên nửa đường tròn đơn vị sao cho (xOM) ̂=120°.
Ta có (MOy) ̂=120°-90°=30°.
Ta tính được tọa độ điểm M((-1)/2;√3/2).
Vậy theo định nghĩa ta có:
sin⁡〖120°=√3/2〗;cos⁡〖120°=(-1)/2〗;
tan⁡〖120°=-√3〗;cot⁡〖120°〗=√3/3
Cho (xOM) ̂=α trên nửa đường tròn đơn vị. Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị và xét dấu của giá trị sinx, cosx trong mỗi trường hợp sau:
a) (xOM) ̂=α=90^o
b) (xOM) ̂=α<90^o
d) (xOM) ̂=α=90^o
Chú ý:
a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.
Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
b) tanα chỉ xác định khi α ≠ 90°, tanα chỉ xác định khi α ≠ 0° và α ≠ 180°.
THỰC HÀNH 1:
Trả lời:
Lấy điểm M trên nửa đường tròn đơn vị sao cho (xOM) ̂ = 135°, H là hình chiếu vuông góc của M trên Oy.
Ta có: (MOy) ̂ = 135° - 90° = 45°.
Tam giác OMH vuông cân tại H nên
OH = MH = OM/√2 = 1/√2 = √2/2.
⇒ Tọa độ điểm M là (-√2/2; √2/2)
Vậy theo định nghĩa ta có:
sin135° = √2/2; cos135° = -√2/2; tan135° = -1; cot135° = -1
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
HĐKP 2:
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4).
Tính tổng số đo của hai góc (xOM) ̂ và (xON) ̂.
Trả lời:
Gọi H là chân đường vuông góc hạ từ N xuống Ox.
Ta có: (NOH) ̂ = (ONM) ̂ = (OMN) ̂ = (MOx) ̂ = α (do NM // Ox)
mà (xON) ̂ + (NOH) ̂ = 180°
⟹ (xON) ̂ + (xOM) ̂ = 180°
KẾT LUẬN
Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° - α) = sin α;
cos(180° - α) = - cos α;
tan(180° - α) = - tan α (α ≠ 90°)
cot(180° - α) = - cot α (0° < α < 180°)
Ví dụ 2 (SGK - tr63)
Cho biết sin30°=1/2;cos45°=√2/2;tan60°=√3.
Tính sin150°;cos135°;tan120°.
Trả lời:
Cho biết sin30°=1/2;cos45°=√2/2;tan60°=√3.
sin150°=sin⁡(180°-30°)=sin30°=1/2;
cos135°=-cos45°=-√2/2;
tan120°=-tan60°=-√3.
Sử dung tính chất của hai góc bù nhau, ta có thể tính giá trị lượng giác của các góc lớn hơn 90° bằng cách đưa về giá trị lượng giác của các góc nhỏ hơn 90°.
THỰC HÀNH 2:
Tính các giá trị lượng giác: sin120°; cos150°; cot135°.
Trả lời:
sin120° = sin(180° - 60°) = sin60° = √3/2
cos150° = -cos(180° - 30°) = -cos30° = - √3/2
cot135° = -cot(180° - 45°) = - cot 45° = -1
VẬN DỤNG 1:
Cho biết sinα =1/2 , tìm góc α (0° ≤ α ≤ 180°) bằng cách vẽ nửa đường tròn đơn vị.
Trả lời:
Do sin α = 1/2 nên tung độ của M bằng 1/2.
Vậy ta xác định được hai điểm N và M trên nửa đường tròn đơn vị, thỏa mãn sin (xON) ̂ = sin(xOM) ̂ = 1/2.
Đặt α = (xOM) ̂ ⟹ (xON) ̂ = 180° - α.
Xét tam giác OHM vuông tại H ta có:
sinα=MH/OM=1/2⇒α=30^o=(xOM) ̂
Vậy α = 30° hoặc α = 150°
3. Giá trị lượng giác của một số góc đặc biệt
Vận dụng tính chất của hai góc bù nhau và kết quả các bài toán trên hãy điền giá trị lượng giác thích hợp vào ô trống.
THỰC HÀNH 3:
Tính
A = sin150° + tan135° + cot45°;
B = 2cos30° – 3tan150° + cot135°.
Trả lời:
A = sin150° + tan135° + cot45°
= 1/2 + (-1) + 1 = 1/2
B = 2cos30° - 3tan150° + cot135°
= 2. √3/2 - 3. (-√3/3) + (-1) = 2√3 - 1
VẬN DỤNG 2:
Tìm gócα (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) sinα = √3/2;
b) cosα = (-√2)/2 ;
c) tanα = –1
d) cotα =-√3
Trả lời:
a) α = 60° hoặc α = 120°
b) α = 135°
c) α = 135°
c) α = 135°
4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
a) Tính các giá trị lượng giác của góc
Ví dụ 3 (SGK - tr64)
Sử dụng máy tính cầm tay, tính sin⁡〖125°34^' 22^''.〗
Trả lời:
Để tính sin⁡〖125°34^' 22^'',〗 ta ân liên tiếp các phím sau đây:
Và được kết quả sin⁡〖125°34^' 22^''≈0,8133603236,〗 với hiển thị trên màn hình như bên
Để tính cosα, tanα ta cũng làm như trên, chỉ thay phím bằng phím
Trường hợp muốn tính cot α, ta tính 1/tan α" " .