Tải giáo án Powerpoint Toán 10 CTST bài: Bài tập cuối chương IX

BÀI TẬP CUỐI CHƯƠNG IX

1. KHỞI ĐỘNG

HS hãy chọn câu trả lời đúng.

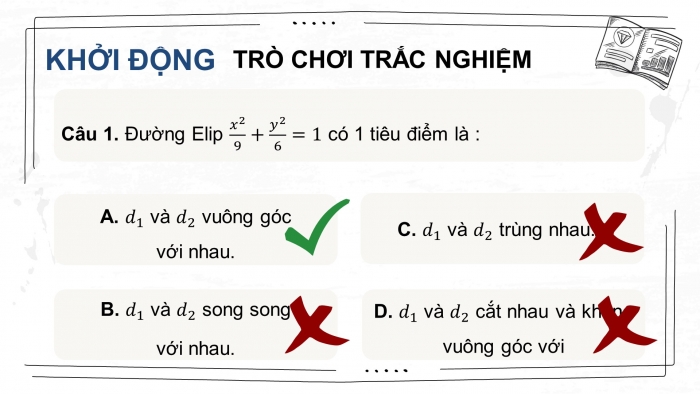
Câu 1. Cho đường thẳng  và . Khẳng định nào sau đây đúng?

1. và vuông góc với nhau.    B.  và  song song với nhau.
2. và trùng nhau.                            D.  và  cắt nhau và không vuông góc với

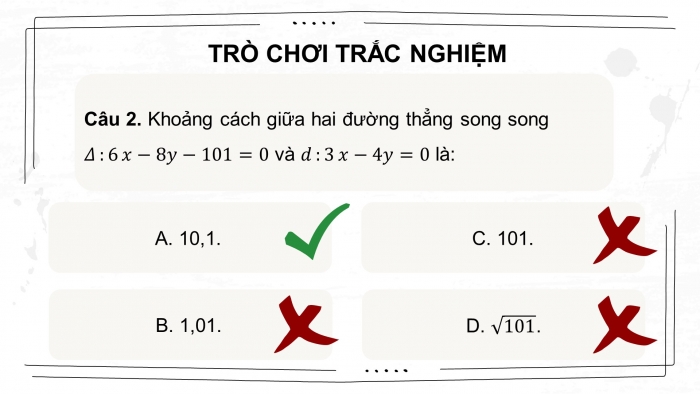
Câu 2. Khoảng cách giữa hai đường thẳng song song  và  là:

1. 10,1. B. 1,01. C. 101.                D. .

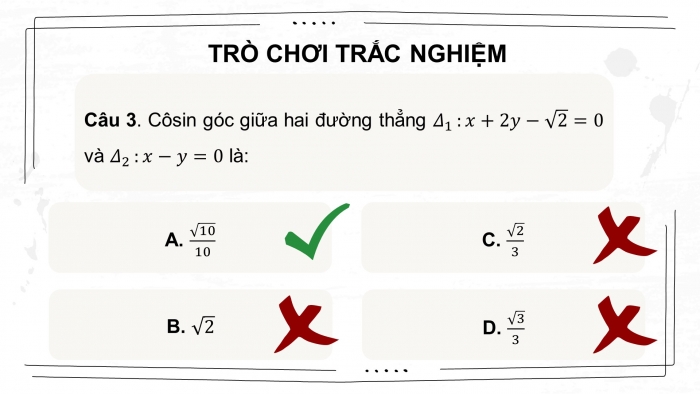
Câu 3. Côsin góc giữa hai đường thẳng  và  là:

1. B. C.                      D.

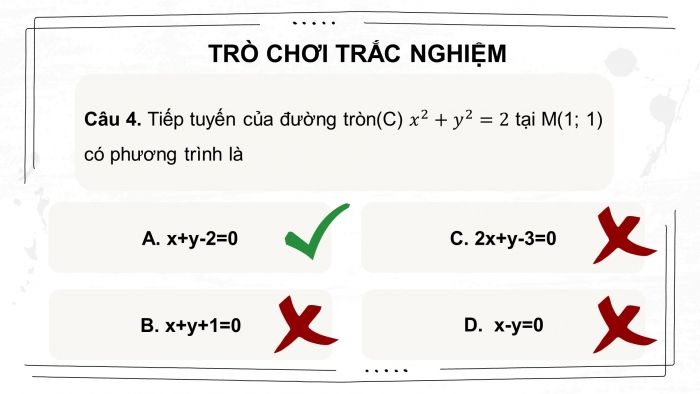
Câu 4. Tiếp tuyến của đường tròn(C)  tại M(1; 1) có phương trình là

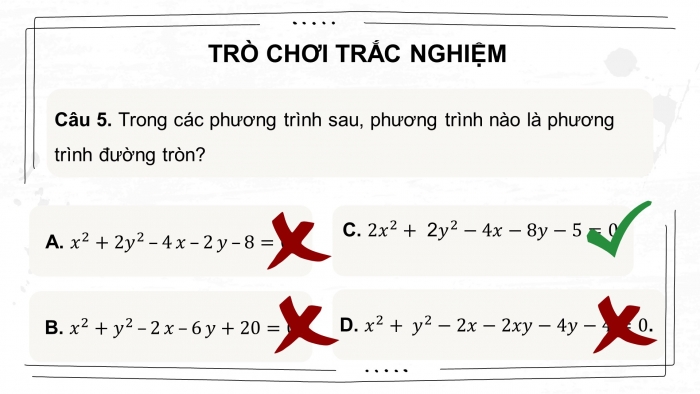
Câu 5. Trong các phương trình sau, phương trình nào là phương trình đường tròn?

1. . B. .
2. .   D. .

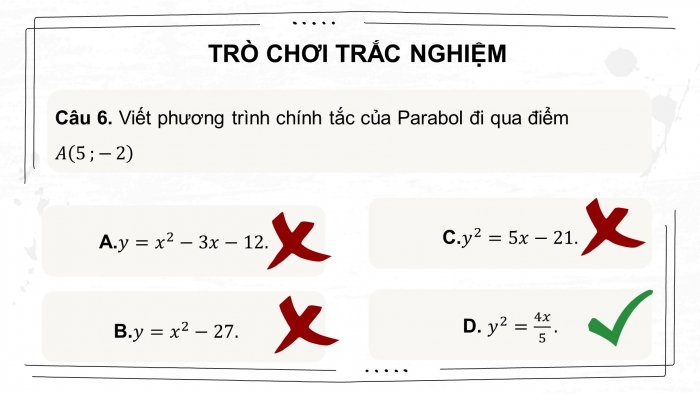
Câu 6. Viết phương trình chính tắc của Parabol đi qua điểm  

1. B.    
2. D.  

Đáp án câu trắc nghiệm:

1. NỘI DUNG BÀI HỌC

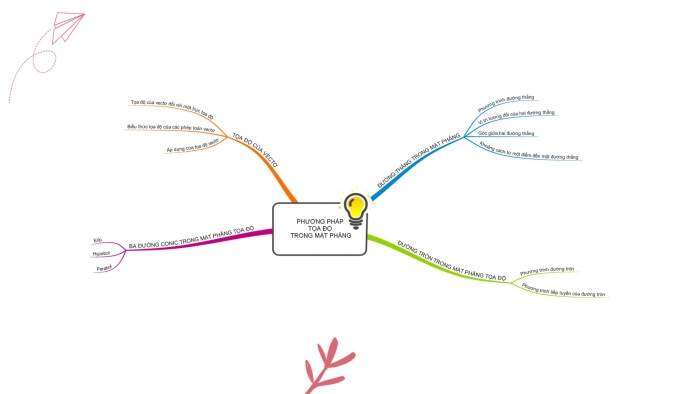
Sơ đồ tổng kết nội dung cơ bản của chương IX

(Có slide)

1. LUYỆN TẬP

Bài 1. (SGK – trang 73)

Trong mặt phẳng , cho bốn điểm , .

1. a) Chứng minh là một hình vuông.
2. b) Tìm toạ độ tâm của hình vuông .

Giải :

1. a) Ta có: = (-1; 3), = (-1; 3)   =  

 ABCD là hình bình hành.

Lại có:  = (3; 1)  .  = -1. 3 + 3. 1 = 0

    hay AB  AD

 Hình bình hành ABCD là hình chữ nhật.

Ta có: AD = || =  =

          AB = || =  =

 AB = AD  Hình chữ nhật ABCD là hình vuông (đpcm).

1. b) Tâm I của hình vuông ABCD là trung điểm của AC I = (; ) I = (3; 3)

Vậy I = (3; 3).

Bài 2. (SGK – trang 73)

Cho  và  là hai dây cung vuông góc tại  của đường tròn . Vẽ hình chữ nhật . Dùng phương pháp toạ độ để chứng minh  vuông góc với .

Giải:

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

Vì ACEF là hình chữ nhật nên F(a; c). 

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

 K là trung điểm của AB  K = (; 0)

     H là trung điểm của CD  H = (0; )

 I = (; )

Ta có:  = (a - ; -) = (; -)

          = ( -; c - ) = (-; 

Vì IA = IC (=R)   +  =  + 

  +  =  +

  = 

 4ab = 4cd  ab = cd  ab - cd = 0

Ta có:  = (-a; -c},  = (-b; d)

 .  = (-a).(-b) - c.d = ab - cd = 0 (chứng minh trên)

    hay EF  BD (đpcm).

Bài 3.

Tìm toạ độ giao điểm và góc giữa hai đường thẳng  và  trong mỗi trường hợp sau:

1. a) và ;
2. b) và ;
3. c) và

Giải

1. a) Đường thẳng và có vectơ pháp tuyến lần lượt là  = (1; -1) và  = (1; 1).

Ta có: .  = 1. 1 + (-1). 1 = 0 nên  và  là hai vectơ vuông góc

     (, ) = .

Giao điểm M của  và  là nghiệm của hệ phương trình: 

Vậy  và  vuông góc và cắt nhau tại M(-3; -1).

1. b) Ta có: = (1; 2) là vectơ chỉ phương của   = (2; -1) là vectơ pháp tuyến của .

Phương trình tổng quát của  đi qua điểm A(1; 3) và nhận  = (2; -1) làm vectơ pháp tuyến là:   

Đường thẳng  có vectơ pháp tuyến là  = (1; -3)

Ta có:      và  là hai vectơ không cùng phương.

  và  cắt nhau. Giao điểm M của  và  là nghiệm của hệ phương trình: