Tải giáo án Powerpoint Toán 10 CTST bài 2: hệ bất phương trình bậc nhất hai ẩn

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY

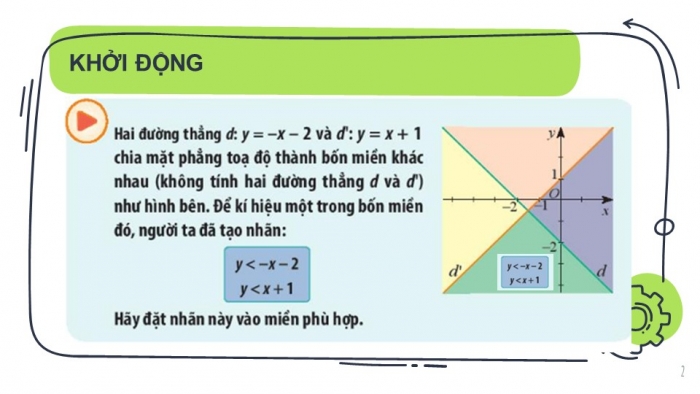
KHỞI ĐỘNG

CHƯƠNG II:

BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬCNHẤT HAI ẨN

BÀI 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT  HAI ẨN

NỘI DUNG

Khái niệm hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn.

Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác.

Luyện tập.

1. Khái niệm hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn.

Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.

1. a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.
2. b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên? (20; 40),  (40; 20), (-30; 10).

HĐKP 1:

Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.

1. a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.

1. b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên?

(20; 40),  (40; 20), (-30; 10).

1. a)
2. b) Cặp số (20; 40) thỏa mãn đồng thời tất cả các bất phương trình nêu trên.

HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN

KẾT LUẬN

Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y.

Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Trên mặt phẳng tọa độ Oxy, tập hợp các điểm  có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.

Tìm hệ bất phương trình bậc nhất hai ẩn trong các hệ sau:

Trả lời:

Các hệ bất phương trình bậc nhất hai ẩn là a); c); d).

Hệ b) không phải là hệ bất phương trình bậc nhất hai ẩn vì hệ này chỉ gồm các phương trình bình thường.

THỰC HÀNH 1

Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.

Trả lời:

1. a) (0; 0) và (0; 1) là hai nghiệm của bất phương trình.
2. c) (0; 0) và (1; -1) là hai nghiệm của bất phương trình.
3. d) (0; 1) và ( 1; 1) là hai nghiệm của bất phương trình.
4. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

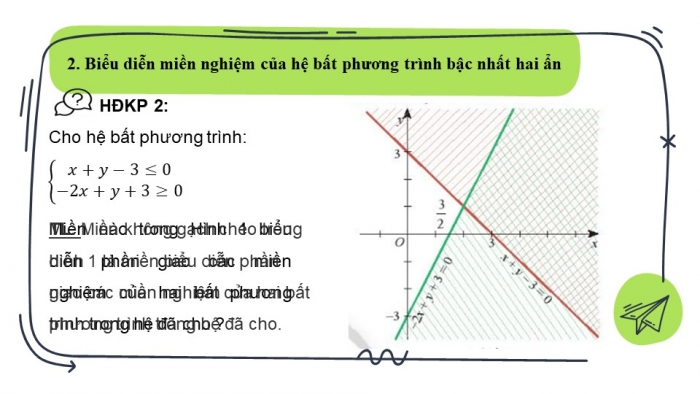
HĐKP 2:

Cho hệ bất phương trình:

TL: Miền không gạch chéo trong hình 1 là miền biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho.

Làm thế nào để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn?

KẾT LUẬN

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ Oxy, ta thực hiện như sau:

- Trên cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.

- Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.

Ví dụ 2:

Biểu diễn miền nghiệm của hệ

Trả lời:

+ Biểu diễn miền nghiệm của bất phương trình  và .

+ Lấy giao của hai miền nghiệm của hai bất phương trình trên.

Chú ý bất phương trình để xét miền nghiệm có lấy cả bờ là đường thẳng hay không.

Ví dụ 3:

Biểu diễn miền nghiệm của hệ bất phương trình

Trả lời:

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng  

VÍ DỤ

Miền nghiệm của hệ bất phương trình trong Ví dụ 3 là miền tứ giác OABC.

Chú ý:

Miền đa giác là miền mặt phẳng tọa độ bao gồm một đa giác lồi và phần nằm bên trong đa giác đó.

THỰC HÀNH 2

Biểu diễn miền nghiệm của hệ bất phương trình : 

Trả lời:

+ Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.

+ Miền không tô màu (miền tứ giác OABC, bao gồm các cạnh) là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by

 trên một miền đa giác

NHẬN XÉT

Tổng quát, người ta chứng minh được rằng giá trị lớn nhất (hay nhỏ nhất) của biểu thức F(x; y) = ax + by, với (x; y) là tọa độ các điểm thuộc miền đa giác , tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.

Ví dụ 4: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công việc cho việc trồng ngô và đậu xanh.

Trả lời:

Gọi x là số hecta trồng ngô và y là số hecta trồng đậu xanh. Ta có:

• Hiển nhiên
• Diện tích canh tác không vượt quá 8 ha nên

Từ đó, ta có hệ bất phương trình:

Biểu diễn miền nghiệm của các bất phương trình trên hệ trục tọa độ  thu được miền tứ giác . Tọa độ các đỉnh của tứ giác đó là:

Gọi  là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: .

Tìm  thỏa mãn hệ bất phương trình sao cho  đạt giá trị lớn nhất của biểu thức

 trên miền tứ giác

Tính các giá trị của biểu thức  tại các đỉnh của đa giác, ta có:

Tại  

Tại

Tại

Tại

 đạt giá trị lớn nhất bằng  tại .

Vậy để thu được nhiều tiềnn hất, bác Năm cần trồng 6 ha  ngô và 2 ha đậu xanh.

Các bước khai giải bài toán tìm cực trị của biểu thức F = ax + by trên một miền đa giác:

+ Bước 1: Đặt x, y cho ẩn số cần tìm.

+ Bước 2: Lập hệ bất phương trình mô tả các điều kiện ràng buộc.

+ Bước 3: Xác định tọa độ đỉnh của miền đa giác biểu diễn miền nghiệm của hệ bất phương trình.

+ Bước 4: Tính giá trị của biểu thức F = ax + by tại các đỉnh của đa giác để tìm giá trị lớn nhất hoặc giá trị nhỏ nhất.

+ Bước 5: Nêu kết luận phù hợp với yêu cầu của bài toán.

Ví dụ 5: Một người dùng ba loại nguyên liệu A,B,C để sản xuất ra hai loại sản phẩm P và Q. Để sản xuất ra 1 kg mỗi loại sản phẩm P và Q phải dùng một số kilogam nguyên liệu khác nhau. Tổng số kilogam nguyên liệu mỗi loại mà người đó có và số kilogam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho tròn bảng sau:

Biết 1 kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất.

Trả lời:

Gọi x là số kilogam sản phẩm P và y là số kilogam sản phẩm Q. Ta có hệ bất phương trình:

Biểu diễn miền nghiệm của các bất phương trình trên hệ trục tọa độ Miền nghiệm là ngũ giác . Tọa độ các đỉnh của tứ giác đó là:

Gọi  là số tiền lãi (đơn vị: triệu đồng) thu được, ta có: .

Tính các giá trị của biểu thức  tại các đỉnh của đa giác, ta có:

Tại

Tại

Tại

Tại

Tại

 đạt giá trị lớn nhất bằng  tại .

Vậy người đó cần sản xuất 4 kg sản phẩm P và 1 kg sản phẩm Q để có lãi cao nhất là 17 triệu đồng.

VẬN DỤNG

Một người bán nước giải khát đang có 24 g bột cam, 9 l nước và 210 g đường để pha chế hai loại nước cam A và B. Để pha chế 1 l nước cam loại A cần 30 g đường, 1 l nước và 1 g bột cam; để pha chế 1 l nước cam loại B cần 10 g đường, 1 l nước và 4 g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất ?

              Gọi  và  là số lít nước cam loại  và  người bán cần pha chế. Ta có hệ bất phương trình mô tả điều kiện ràng buộc:

Miền nghiệm là đa giác có toạ độ các đỉnh là .

Gọi  là số tiền (đơn vị: nghìn đồng) người đó thu được.

Ta có . Tính giá trị của  tại các đỉnh, ta thấy  đạt giá trị lớn nhất bằng 640 nghìn đồng tại đỉnh .

Vậy người bán nên pha chế  nước cam loại  và  nước cam loại  thì có doanh thu cao nhất.