Tải giáo án Powerpoint Toán 10 CTST bài 3: Các phép toán trên tập hợp

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!
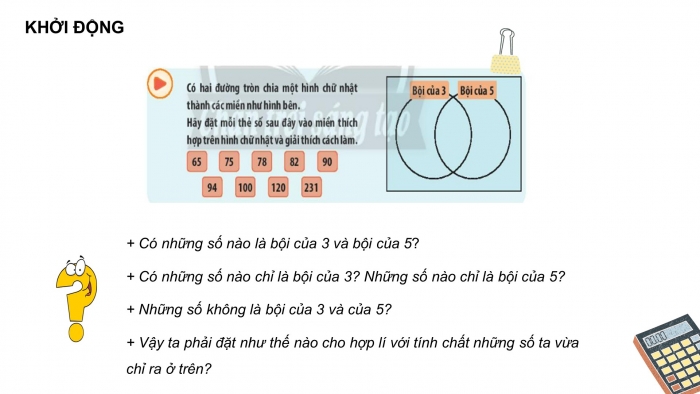
KHỞI ĐỘNG
+ Có những số nào là bội của 3 và bội của 5?
+ Có những số nào chỉ là bội của 3? Những số nào chỉ là bội của 5?
+ Những số không là bội của 3 và của 5?
+ Vậy ta phải đặt như thế nào cho hợp lí với tính chất những số ta vừa chỉ ra ở trên?
CHƯƠNG I: MỆNH ĐỀ VÀ TẬP HỢP
BÀI 3: CÁC PHÉP TOÁN TRÊN TẬP HỢP
NỘI DUNG
HỢP VÀ GIAO CỦA CÁC TẬP HỢP
HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP CON
LUYỆN TẬP
HỢP VÀ GIAO CỦA CÁC TẬP HỢP
HĐKP 1:
Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):
a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về mặt ngoại ngữ.
b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.
a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về mặt ngoại ngữ.
Trả lời:
A={a_1;a_2;a_5;a_6;a_7;a_8;a_10 },
B={a_1;a_3;a_5;a_6;a_8;a_10 }.

b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
Trả lời:
C={a_1;a_5;a_6;a_8;a_10 }.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.
Trả lời:
D={a_1;a_2;a_3;a_5;a_6;a_7;a_8;a_10 }.
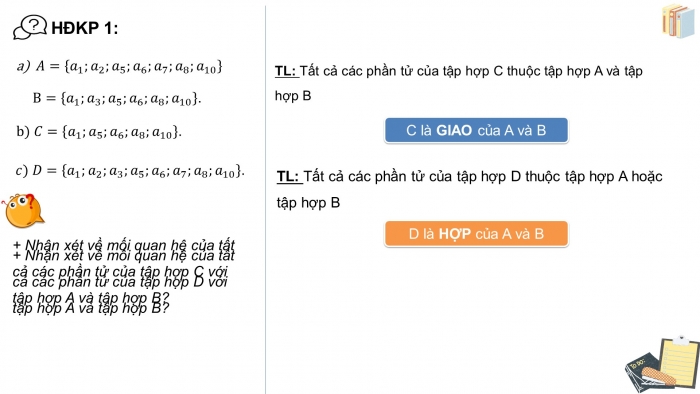
HĐKP 1:
A={a_1;a_2;a_5;a_6;a_7;a_8;a_10 }
B={a_1;a_3;a_5;a_6;a_8;a_10 }.
b) C={a_1;a_5;a_6;a_8;a_10 }.
c) D={a_1;a_2;a_3;a_5;a_6;a_7;a_8;a_10 }.
+ Nhận xét về mối quan hệ của tất cả các phần tử của tập hợp D với tập hợp A và tập hợp B?
TL: Tất cả các phần tử của tập hợp C thuộc tập hợp A và tập hợp B
C là GIAO của A và B
TL: Tất cả các phần tử của tập hợp D thuộc tập hợp A hoặc tập hợp B
D là HỢP của A và B
KẾT LUẬN
Cho hai tập hợp A và B
Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A∪B.
A∪B={x|x∈Ahoặc x∈B}.
Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A∩B.
A∩B={x|x∈Avà x∈B}.
VÍ DỤ 1:
Xác định A∪B và A∩B trong mỗi trường hợp sau
a) A= {2;3;5;7}, B= {1;3;5;15}
b) A={x∈R|x(x+2)=0}, B={x∈R|x^2+2=0}
c) A là tập hơp các hình bình hành, B là tập hợp các hình thoi.
+ Hợp và giao của tập hợp A và tập rỗng là gì?
A∪∅=A,A∩∅=∅
+ Nếu B⊂A thì hợp và giao của tập hợp A và B là gì?
A∪B=A,A∩B=B
Giải:
a) A∪B={1;2;3;5;7;15}, A∩B={3;5}
b) A={-2;0}, B={∅}
A∪B=A∪∅=A={-2;0}
A∩B=A∩∅=∅
c) B⊂A
A∪B=A, A∩B=B
VÍ DỤ 2:
Lớp 10D có 22 bạn chơi bóng đá, 25 bạn chơi cầu lông và 15 bạn chơi cả hai môn thể thao này. Hỏi lớp 10D có bao nhiêu học sinh chơi ít nhất một trong hai môn thể thao bóng đá và cầu lông.
Giải:
Kí hiệu A,B lần lượt là tập hợp các học sinh của lớp 10D chơi bóng đá, chơi cầu lông.
Theo giả thiết n(A)=22, n(B)=25, n(A∩B)=15
Tập hợp số học sinh chơi ít nhất một trong hai môn thể thao bóng đá và cầu lông có mối quan hệ gì với A và B?
VÍ DỤ 2:
Lớp 10D có 22 bạn chơi bóng đá, 25 bạn chơi cầu lông và 15 bạn chơi cả hai môn thể thao này. Hỏi lớp 10D có bao nhiêu học sinh chơi ít nhất một trong hai môn thể thao bóng đá và cầu lông.
Giải:
Kí hiệu A,B lần lượt là tập hợp các học sinh của lớp 10D chơi bóng đá, chơi cầu lông.
Theo giả thiết n(A)=22, n(B)=25, n(A∩B)=15
Nếu tính tổng n(A)+ n(B) thì ta được số học sinh lớp 10D chơi bóng đá hoặc cầu lông, nhưng số bạn chơi cả 2 môn được tính hai lần.
Từ biểu đồ Ven, nhận xét mối quan hệ n(A), n(B) và n(A∩B),n(A∪B).
Do đó số chơi ít nhất một trong hai môn là:
n(A∪B)=n(A)+" " n(B)-n(A∩B)=22+25-15=32.
Nhận xét:
- Nếu A và B là hai tập hợp hữu hạn thì n(A∪B)=n(A)+n(B)-n(A∩B)
- Nếu A và B không có phần tử chung, tức A∩B=∅, thì n(A∪B)=n(A)+n(B)
THỰC HÀNH 1
Xác định tập hợp A ∪ B và A ∩ B, biết:
a) A = {a; b; c; d; e}, B = {a; e; i; u};
b) A = {x ∈ ℝ| x2 + 2x – 3 = 0},
B = {x ∈ ℝ | |x| = 1}.
Giải:
a) A∪B={a;b;c;d;e;i;u},
A∩B={a;e}.
b) A={-3;1},B={-1;1}.
Từ đó, A∪B={-3;-1;1},A∩B={1}.
THỰC HÀNH 2
Cho A = {(x; y)| x, y ∈ ℝ , 3x – y = 9}, B = {(x; y)| x, y ∈ ℝ , x – y = 1}.
Hãy xác định A ∩ B.
Giải:
Ta thấy (x;y)∈A∩B,
x và y phải thoả mãn {■(3x-y=9@x-y=1.)┤
Vậy A∩B={(4;3)}.
VẬN DỤNG
Tại vòng chung kết của một trò chơi truyền hình, có 100 khán giải tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rẳng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh này. Có bao nhiêu khán giá đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?
Giải:
Kí hiệu E là tập hợp các khán giả bình chọn cho thí sinh A,F là tập hợp các khán giả bình chọn cho thí sinh⁡B.
Theo giả thiết, ta có n(E)=85,n(F)=72 và n(E∩F)=60.
Tập hợp các khán giả đã bình chọn chính là E∪F. Ta có
n(E∪F)=n(E)+n(F)-n(E∩F)=85+72-60=97.
Vậy có 97 khán giả đã tham gia bình chọn và 3 khán giả không tham gia bình chọn.
HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP CON
HĐKP 2: Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở hoạt động khám phá 1.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
Trả lời E={a_2;a_7 }
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
Trả lời F={a_3;〖_4a〗;a_9 }.
A={a_1;a_2;a_5;a_6;a_7;a_8;a_10 },
B={a_1;a_3;a_5;a_6;a_8;a_10 }.
Nhận xét về mối quan hệ giữa các phần tử của tập F và tập hợp A và tập hợp các ứng viên tham gia phỏng vấn gọi là tập M?
KẾT LUẬN
Cho hai tập hợp A và B.
Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\B.
A\B={x|x∈A và x∉B}.
Nếu A là tập con của E thì hiệu E\A gọi là phần bù của A trong E, kí hiệu C_E A.
Chú ý: Hiệu của B và A khác với hiệu của A và B.
VÍ DỤ 3:
Cho E={x∈N | x<10}, A= {0;2;4;6;8} , B={0;3;6;9}
Xác định các tập hợp A\B, B\A,C_E A,C_E B.
Giải:
Ta có:
A\B={2;4;8}
B\A={3;9}
C_E A={1;3;5;7;9}
C_E B={1;2;4;5;7;8}
THỰC HÀNH 3
Cho các tập hợp E = {x ∈ ℕ | x < 8}, A = {0; 1; 2; 3; 4}, B = {3; 4; 5}.
Xác định các tập hợp sau đây:
A\B, B\A và (A\B) ∩ (B\A);
CE(A ∩ B) và (CEA) ∪ (CEB);
CE(A ∪ B) và (CEA) ∩ (CEB).
Giải:
a) A∖B={0;1;2},B∖A={5}, (A∖B)∩(B∖A)=∅.
b) A∩B={3;4}, C_E (A∩B)={0;1;2;5;6;7}
C_E A={5;6;7}, C_E B={0;1;2;6;7" " }
(C_E A)∪(C_E B)={0;1;2;5;6;7}.
Nhận xét: C_E (A∩B)=(C_E A)∪(C_E B).
THỰC HÀNH 3
Cho các tập hợp E = {x ∈ ℕ | x < 8}, A = {0; 1; 2; 3; 4}, B = {3; 4; 5}.
Xác định các tập hợp sau đây:
A\B, B\A và (A\B) ∩ (B\A);
CE(A ∩ B) và (CEA) ∪ (CEB);
CE(A ∪ B) và (CEA) ∩ (CEB).
Nhận xét: C_E (A∩B)=(C_E A)∪(C_E B).
C_E (A∪B)=(C_E A)∩(C_E B)
Giải:
a) A∖B={0;1;2},B∖A={5}, (A∖B)∩(B∖A)=∅.
b) A∩B={3;4}, C_E (A∩B)={0;1;2;5;6;7}
C_E A={5;6;7}, C_E B={0;1;2;6;7" " }
(C_E A)∪(C_E B)={0;1;2;5;6;7}.
c) A∪B={0;1;2;3;4;5}, C_E (A∪B)=6;7
(C_E A)∩(C_E B)={6;7}.
Để tìm các tập hơp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số.
VÍ DỤ 4:
Xác định các tập hợp sau đây
■(a)"   " A=[-2;1)" " ∪" " (0;3];"                 " b)" " B=" " (-∞;1]∪(-2;2)"                " c)" " C=" " (-1;4]∩(-3;2);@d)"  " D="  " (-3;2)\(1;4);"                  " e)" " E=C_R (-∞;2) )
Giải:
a) Để xác định tập hợp A, ta vẽ sơ đồ sau đây:
THỰC HÀNH 4
Xác định các tập hợp sau đây:
a) (1; 3) ∪ [-2; 2];
b) (-∞;1)∩[0;π];
c) [1/2;3)\\(1;+∞);
d) C_R [-1;+∞)
Giải:
a) [-2;3)
b) [0;1)
c) [1/2;1]
d) (-∞;-1)
LUYỆN TẬP
Bài 1 (SGK – tr25)
Xác định các tập hợp A ∪ B và A ∩ B với:
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím};
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
Giải
a) A∩B={lục; lam}, A∪B={đỏ; cam; vàng; lục; lam; chàm; tím}.
b) Ta thấy A⊂B. Từ đó, A∪B=B,A∩B=A.
Bài 2 (SGK – tr25)
Xác định tập hợp A ∩ B trong mỗi trường hợp sau:
a) A = {x ∈ ℝ | x2 – 2 = 0}, B = {x ∈ ℝ | 2x – 1 < 0};
b) A = {(x; y)| x, y ∈ ℝ , y = 2x – 1}, B = {(x; y)| x, y ∈ ℝ, y = - x + 5};
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
Giải
a) A={-√2;√2},B=(-∞;1/2),A∩B={-√2}.
b) A∩B={(2;3)}.
c) A∩B là tập hợp các hình vuông.
Bài 3 (SGK – tr25)
Cho E = {x ∈ N | x < 10}, A = {x ∈ E| x là bội của 3},
B = {x ∈ E| x là ước của 6}.
Xác định các tập hợp A\B, B\A, CEA, CEB, CE(A∪B), CE(A∩B).
Giải
A={0;3;6;9},B={1;2;3;6}
A∪B={0;1;2;3;6;9},
A∩B={3;6}
A∖B={0;9}
B∖A={1;2}
C_E A={1;2;4;5;7;8}
C_E B={0;4;5;7;8;9}
C_E (A∩B)={0;1;2;4;5;7;8;9}
C_E (A∪B)={4;5;7;8}
Bài 4 (SGK – tr25)
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và A∪B;
b) A và A∩B.
Giải
Ta có sơ đồ ven sau:
a) A⊂(A∪B).
b) (A∩B)⊂A.
Bài 5 (SGK – tr25)
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích học môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) có bao nhiêu học sinh không thích cả hai môn này?
Giải
Kí hiệu A là tập hợp các học sinh lớp 10H thích môn Toán, B là tập hợp các học sinh lớp 10H thích môn Tiếng Anh.
Ta có: n(A)=20,n(B)=16,n(A∩B)=12.
a) Số học sinh của lớp 10H thích it nhất một trong hai môn này là
n(A∪B)=n(A)+n(B)-n(A∩B)=20+16-12=24.
b) Số học sinh không thích cả hai môn này là
35-n(A∪B)=35-24=11
BÀI TẬP VỀ NHÀ
Bài 1: Cho hai tập khác rỗng A = (m-1; 4] và B = (-2; 2m+2), với m∈R.
Xác định m để:
a) A∩B≠∅
b) A⊂B
c) B⊂A
d) (A∩B)⊂(-1 ;⁡3)
Bài 2. Mỗi học sinh của lớp 10A đều biết chơi cờ tướng hoặc cờ vua, biết rằng có 25 em biết chơi cờ tướng, 30 em biết chơi cờ vua, 15 em biết chơi cả hai. Hỏi lớp 10Acó bao nhiêu em chỉ biết chơi cờ tướng, bao nhiêu em chỉ biết chơi cờ vua? Sĩ số lớp là bao nhiêu?
HƯỚNG DẪN VỀ NHÀ
Ghi nhớ kiến thức trong bài.
Hoàn thành các bài tập trong SBT
Chuẩn bị bài mới “Bài tập cuối chương I".
GV chia lớp làm các tổ (4 – 5 tổ), mỗi tổ sẽ thực hiện vẽ một sơ đồ tổng kết kiến thức của chương I.
HS về nhà chuẩn bị trước các bài tập (SGK – tr27).
HẸN GẶP LẠI CÁC EM Ở TIẾT HỌC SAU!