Tải giáo án Powerpoint Toán 10 CTST bài 2: Định lí cosin và định lí sin

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY
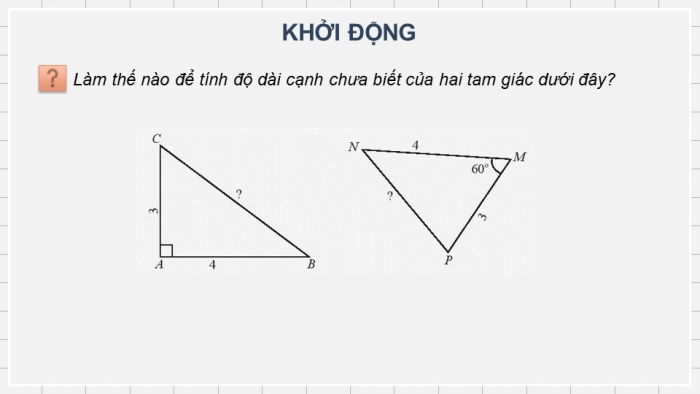
KHỞI ĐỘNG
Làm thế nào để tính độ dài cạnh chưa biết của hai tam giác dưới đây?
CHƯƠNG IV:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
BÀI 2: ĐỊNH LÍ COSIN VÀ ĐỊNH LÍ SIN
NỘI DUNG
Định lí côsin trong tam giác
Định lí sin trong tam giác
Các công thức tính diện tích tam giác
Luyện tập
Định lí côsin trong tam giác
HĐKP 1:
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và C ̂≥B ̂. Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức a2 = b2 + c2 – 2bccosA theo gợi ý sau:
Xét tam giác vuông BCD, ta có:
a2 = d2 + (c – x)2 = d2 + x2 + c2 – 2xc (1)
Xét tam giác vuông ACD, ta có:
b2 = d2 + x2 ⇒ d2 = b2 – x2 (2)
cosA=?/b ⇒ ? =bcosA (3)
Thay (2) và (3) vào (1), ta có: a2 = b2 + c2 – 2bccosA.
HĐKP 1:
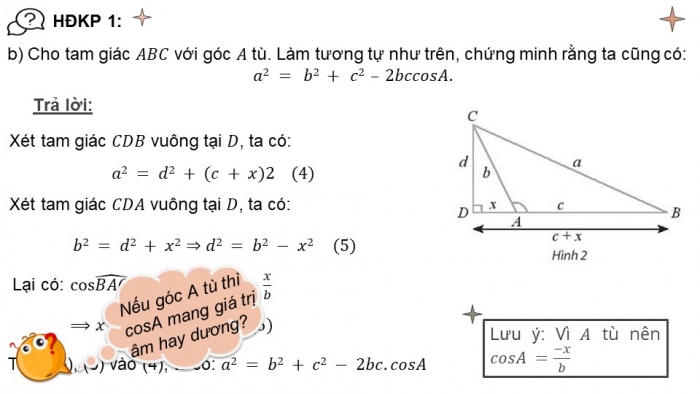
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
a2 = b2 + c2 – 2bccosA.
Trả lời:
Xét tam giác CDB vuông tại D, ta có:
a2 = d2 + (c + x)2 (4)
Xét tam giác CDA vuông tại D, ta có:
b2 = d2 + x2 ⇒ d2 = b2 - x2 (5)
Lại có:
⟹ x = -bcosA (6)
Thay (5), (6) vào (4), ta có: a2 = b2 + c2 - 2bc.cosA
Lưu ý: Vì A tù nên cosA =(-x)/b
HĐKP 1:
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức a2 = b2 + c2 – 2bccosA có thể viết là a2 = b2 + c2.
Trả lời:
c) Tam giác ABC vuông tại A ⟹A ̂ = 90°.
Ta có: a2 = b2 + c2 - 2bc.cosA
a2 = b2 + c2 - 2bc.cos90°
 a2 = b2 + c2
KẾT LUẬN
Định lí côsin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
a2 = b2 + c2 - 2bc cosA;
b2 = c2 + a2 - 2ca cosB;
c2 = a2 + b2 - 2ab cosC.
Hệ quả:
cosA = (b^2+c^2-a^2)/2bc; cosB = (c^2+a^2-b^2)/2ca;
cosC = (a^2+b^2-c^2)/2ab.
Ví dụ 1 (SGK - tr66)
Cho tam giác ABC có C ̂=115°, AC=8, BC=12. Tính độ dài cạnh AB và các góc A,B của tam giác đó.
Trả lời:
Theo định lí côsin, ta có:
AB^2=BC^2+AC^2-2.BC.AC.cos⁡C
=12^2+8^2-2.12.8.cos115°
≈289,14.
Vậy AB≈√289,14 ≈17.
Theo hệ quả của định lí côsin, ta có:
cos⁡A=(AB^2+AC^2-BC^2)/(2.AB.AC)≈(17^2+8^2-12^2)/2.17.18≈0,7684.
Suy ra A ̂≈39°47^', B ̂=180°-(A ̂+C ̂)≈25°13'.
THỰC HÀNH 1
Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình 4.
Trả lời:
Theo định lí côsin, ta có:
BC2 = AC2 + AB2 - 2AC. AB cosA
= 142 + 182 - 2. 14. 18. cos62°
≈ 283,3863
⟹ BC = √283,3863 ≈ 16,834
Theo hệ quả của định lí côsin, ta có:
cosB = (〖AB〗^2+〖BC〗^2-〖AC〗^2)/(2AB. BC) = (14^2+〖16,834〗^2-18^2)/(2.14. 16,834) ≈ 0,3297
cosC = (〖AC〗^2+〖BC〗^2-〖AB〗^2)/(2AC. BC) = (18^2+〖16,834〗^2-14^2)/(2.18. 16,834) ≈ 0,6788
Vậy BC ≈ 16,834; B ̂ ≈ 70°45’; C ̂ ≈ 47°15'
VẬN DỤNG 1
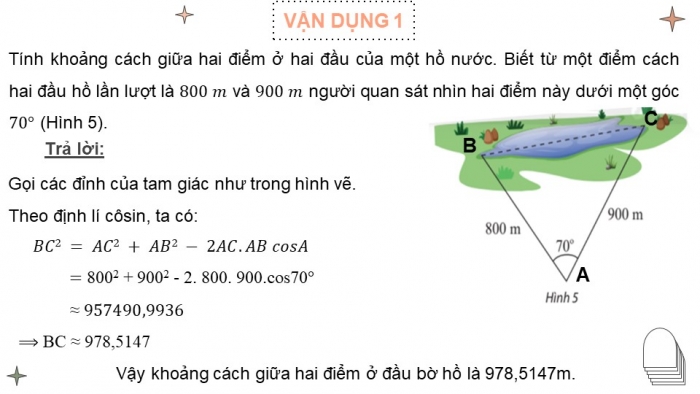
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).
Trả lời:
Gọi các đỉnh của tam giác như trong hình vẽ.
Theo định lí côsin, ta có:
BC2 = AC2 + AB2 - 2AC. AB cosA
= 8002 + 9002 - 2. 800. 900.cos70°
≈ 957490,9936
⟹ BC ≈ 978,5147
Vậy khoảng cách giữa hai điểm ở đầu bờ hồ là 978,5147m.
Định lí sin trong tam giác
HĐKP 2:
a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính sin(BDC) ̂ theo a và R.
ii) Tìm mối liên hệ giữa hai góc (BAC) ̂ và (BDC.) ̂Từ đó chứng minh rằng 2R =a/sinA.
Trả lời:
i) Xét tam giác BDC vuông tại C, ta có: sin(BDC) ̂ = BC/BD = a/2R
ii) Với tam giác ABC có góc A nhọn, ta có:
(BAC) ̂ = (BDC) ̂ (hai góc nội tiếp cùng chắn cung BC).
⟹ sin(BAC) ̂ = sin(BDC) ̂ = a/2R ⟹ 2R = a/sinA.
Với tam giác ABC có góc A tù, ta có tứ giác ABDC nội tiếp đường tròn tâm O.
⟹ (BAC) ̂ + (BDC) ̂ = 180°
⟹ sin(BAC) ̂ = sin(180°-(BDC) ̂) = sin(BDC) ̂ = a/2R ⟹ 2R = a/sinA
Vậy 2R = a/sinA
HĐKP 2:
a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính sin(BDC) ̂ theo a và R.
ii) Tìm mối liên hệ giữa hai góc (BAC) ̂ và (BDC.) ̂Từ đó chứng minh rằng 2R =a/sinA.
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = a/sinA.
Trả lời:
Tam giác ABC vuông tại A nội tiếp đường tròn tâm O bán kính BC/2
⟹ 2R = a (1)
Ta có: sinA = sin90° = 1 (2)
Từ (1) và (2) ⟹ 2R = a/1 = a/sinA
Vậy 2R = a/sinA
KẾT LUẬN
Định lí sin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
a/sinA = b/sinB = c/sinC = 2R
Hệ quả:
a = 2RsinA; b = 2RsinB; c = 2RsinC;
sinA = a/2R; sinB = b/2R; sinC = c/2R
Ví dụ 2 (SGK - tr68)
Cho tam giác ABC có A ̂=72°, B ̂=83, BC=18. Tính độ dài các cạnh AC, AB và bán kính R của đường tròn ngoại tiếp tam giác đó.
Trả lời:
Đặt a=BC, b=AC, c=AB.
Ta có a=18, ( C) ̂=180°-(72°+83°)=25°.
Áp dụng định lí sin, ta có:
a/sinA=b/sinB=c/sinC=2R
Suy ra:
AC=b=asinB/sinA=(18.sin83°)/(sin72°)≈18,8;
AB=c=asinC/sinA=(18.sin25°)/(sin72°)≈8;
R=a/(2.sinA)=18/(2.sin72°)≈9,5.
THỰC HÀNH 2
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
Trả lời:
Ta có: P ̂ = 180° - M ̂ - N ̂
= 180° - 34° - 112° = 34°
⟹ Tam giác MNP cân tại N ⟹ MN = NP = 22
Áp dụng định lí sin trong tam giác, ta có:
NP/sinM = MP/sinN = MN/sinP = 2R
Suy ra: MP = (NP.sinN)/sinM = (22.sin112°)/(sin34°) ≈ 36,5.
VẬN DỤNG 2
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn ?
Trả lời:
Gọi điểm tháp canh là C, điểm cháy là D (như hình vẽ).
Ta có: (BDC) ̂ = 180° - 35° - 125° = 20°
Áp dụng định lí sin cho tam giác CBD, ta có: BD/(sin(BCD) ̂ ) = CB/(sin(BDC) ̂ ) = CD/(sin(CBD) ̂ ) = 2R.
Suy ra: BD = (CB.sin(BCD) ̂)/(sin(BDC) ̂ ) = (900.sin35°)/(sin20°) ≈ 1509,3 (m).
CD = (CB.sin(CBD) ̂)/(sin(BDC) ̂ ) = (900.sin125°)/(sin20°) ≈ 2155,5 (m).
Áp dụng định lí côsin trong tam giác ACD, ta có:
AD2 = CA2 + CD2 - 2AC. CD. cos(ACD) ̂
= 18002 + 2155,52 - 2. 1800. 2155,5. cos34° ≈ 1453014,5.
⟹ AD ≈ 1205, 4(m).
Nhận thấy AD < BD nên dẫn nước từ bồn chứa A sẽ dập tắt đám cháy nhanh hơn.
Các công thức tính diện tích tam giác
Một số kí hiệu trong tam giác
Cho tam giác ABC có:
+ h_a,h_b,h_c là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.
+ R là bán kính đường tròn ngoại tiếp tam giác.
+ r là bán kính đường tròn nội tiếp tam giác.
+ p là nửa chu vi tam giác.
+ S là diện tích tam giác.
Công thức Heron được viết như sau:
Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b và c
S=√(p(p-a)(p-b)(p-c))
Với p=(a+b+c)/2
HĐKP 3:
a) Xét tam giác ABC, đường cao AH: SABC = 1/2. AH. BC = 1/2. ha. a (1)
b) Xét tam giác AHC vuông tại H, ta có: sinC = AH/AC = h_a/b ⟹ ha = b. sinC (2)
c) Thay (2) vào (1), ta được: S = 1/2 absinC.
d) Áp dụng định lí sin, ta có: a/sinA = b/sinB = c/sinC = 2R
⟹ sinC = c/2R
⟹ S = 1/2 absinC = 1/2 ab. c/2R = abc/4R.
Vậy S = abc/4R