Tải giáo án Powerpoint Toán 7 Cánh diều Chương 1 Bài 3. Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC
Khối lượng Trái Đất khoảng 5,9724.10^24 kg.
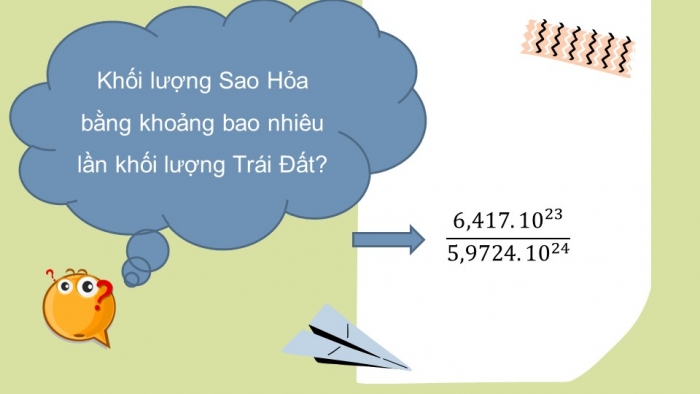
Khối lượng Sao Hỏa khoảng 6,417.10^23kg.
Khối lượng Sao Hỏa bằng khoảng bao nhiêu lần khối lượng Trái Đất?
(6,417.10^23)/(5,9724.10^24 )
BÀI 3: PHÉP TÍNH LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN CỦA MỘT SỐ HỮU TỈ
NỘI DUNG BÀI HỌC
Phép tính luỹ thừa với số mũ tự nhiên
Tích và thương của hai luỹ thừa cùng cơ số
Luỹ thừa của một luỹ thừa
Luyện tập
I. PHÉP LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN
HĐ1
Viết các tích sau dưới dạng luỹ thừa
7.7.7.7.7
⏟(12.12. ….12)┬n thừa số 12
Với n là một số tự nhiên lớn hơn 1, lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x:
x^n=⏟(x.x. ….x)┬n thừa số x (x∈Q,n∈N,n>1)
Số x được gọi là cơ số, n được gọi là số mũ.
Quy ước: x^1=xx^0=1(x≠0)
Chú ý:
xn đọc là "x mũ n" hoặc "x lũy thừa n" hoặc "lũy thừa bậc n của xn"
x2 còn được gọi là "x bình phương" hay "bình phương của x"
x3 còn được đọc là "x lập phương" hay "lập phương của x"
Ví dụ 1
Viết mỗi tích sau dưới dạng một luỹ thừa
(-5)/7.(-5)/7.(-5)/7.(-5)/7=((-5)/7)^4

(-0,4).(-0,4).(-0,4).(-0,4).(-0,4)=(-0,4)^5

* Lưu ý:
Để viết lũy thừa bậc n của phân số a/b, ta phải viết a/b trong dấu ngoặc ( ), tức là (a/b)^n.
(a/b)^n=a^n/b^n
(a,b∈Z,b≠0)
Ví dụ 2
So sánh
((-3)/5)^2 và (-3)^2/5^2
((-3)/5)^2=(-3)/5.(-3)/5=((-3).(-3))/5.5=(-3)^2/5^2 .
〖Vậy((-3)/5)〗^2=(-3)^2/5^2
(2/3)^3 và 2^3/3^3
(2/3)^3=2/3.2/3.2/3=2.2.2/3.3.3=2^3/3^3 .
〖Vậy(2/3)〗^3=2^3/3^3
Luyện tập 1
Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m.
Giải
V=(1,8)^3= 5,832 (m^3)
Luyện tập 1
Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m.
Giải
V=(1,8)^3= 5,832 (m^3)
Luyện tập 2
Tính
((-3)/4)^3
=(-3)/4.(-3)/4.(-3)/4=((-3).(-3).(-3))/4.4.4

(1/2)^5=1/2.1/2.1/2.1/2.1/2=1.1.1.1.1/2.2.2.2.2=1/32.
II. TÍCH VÀ THƯƠNG CỦA HAI LUỸ THỪA CÙNG CƠ SỐ
HĐ2
2^m.2^n=2^(m+n) (m,n∈N)
3^m 〖 :3 〗^n=3^(m-n) (m≥n)
Quy tắc:
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
x^m.x^n=x^(m+n)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia.
x^m:x^n=x^(m-n) (x≠0, m≥n)
Ví dụ 3
Viết kết quả của mỗi phép tính sau dưới dạng một luỹ thừa
((-5)/9)^4.((-5)/9)^3=((-5)/9)^(4+3)=((-5)/9)^7
(-0,8)^5:(-0,8)^2=(-0,8)^(5-2)=(-0,8)^3
Luyện tập 3
Viết kết quả của mỗi phép tính sau dưới dạng một luỹ thừa
6/5.(1,2)^8
=1,2.(1,2)^8
=(1,2)^(1+8)
=(1,2)^9
III. LUỸ THỪA CỦA LUỸ THỪA
So sánh (15^3 )^2 và 15^3.2
Ta có
(15^3 )^2=15^3.15^3=15^(3+3)=15^6
15^3.2=15^6
Vậy (15^3 )^2= 15^3.2
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ:
(x^m )^n=x^(m.n)
Ví dụ 4
Viết kết quả của mỗi phép tính sau dưới dạng luỹ thừa của a.
[((-2)/7)^3 ]^5=((-2)/7)^3.5=((-2)/7)^15=a^15
[(0,1)^2 ]^4=(0,1)^2.4=(0,1)^8=a^8
Ví dụ 5
Viết 2^18 dưới dạng:
Luỹ thừa của 2^2
2^18=2^2.9=(2^2 )^9
Luỹ thừa của 8
2^18=2^3.6=(2^3 )^6=8^6
Luyện tập 4
Viết kết quả của mỗi phép tính sau dưới dạng luỹ thừa của a.
Với a=(-1)/6 ta có:
[((-1)/6)^3 ]^4=(a^3 )^4=(a)^3.4=a^12
Với a=-0,2 ta có:
[(-0,2)^4 ]^5=(a^4 )^5=(a)^4.5=a^20
IV. LUYỆN TẬP
Tìm số thích hợp cho ? trong bảng
So sánh
(-2)^4.(-2)^5 và〖 (-2)〗^12 :(-2)^3
(-2)^4.(-2)^5=(-2)^(4+5)=(-2)^9
(-2)^12:(-2)^3=(-2)^(12-3)=(-2)^9
〖⇒(-2)〗^4.(-2)^5=〖 (-2)〗^12 :(-2)^3
(1/2)^2.(1/2)^6 và[(1/2)^4 ]^2
(1/2)^2.(1/2)^6=(1/2)^(2+6)=(1/2)^8
[(1/2)^4 ]^2=(1/2)^4.2=(1/2)^8
〖⇒(1/2)〗^2.(1/2)^6=[(1/2)^4 ]^2
(0,3)^8:(0,3)^2 và [(0,3)^2 ]^3
(0,3)^8:(0,3)^2=(0,3)^(8-2)=(0,3)^6 ;
[(0,3)^2 ]^3=(0,3)^2.3=(0,3)^6
〖⇒(0,3)〗^8:(0,3)^2= [(0,3)^2 ]^3
(-3/2)^5:(-3/2)^3 và〖 (3/2)〗^2
(-3/2)^5:(-3/2)^3=(-3/2)^(5-3)=(-3/2)^2=(3/2)^2
〖⇒(-3/2)〗^5:(-3/2)^3=〖 (3/2)〗^2
Tìm x, biết
(1,2)^3.x=(1,2)^5
x=(1,2)^5:(1,2)^3
x=(1,2)^2
x=1,44
(2/3)^7:x=(2/3)^6
x=(2/3)^7:(2/3)^6
x=2/3

Viết kết quả của mỗi phép tính sau dưới dạng luỹ thừa của a.
(8/9)^3.4/3.2/3
〖=(8/9)〗^3.8/9=(8/9)^4=a^4 ,với a=8/9
(1/4)^7.0,25
〖=(0,25)〗^7.0,25 =〖0,25〗^8=a^8 ,với a=0,25
(-0,125)^6:(-1)/8
=((-3)/2)^3.2=((-3)/2)^6=a^6 ,với a=(-3)/2
〖=((-1)/8)〗^6:(-1)/8=((-1)/8)^5=a^5,
với a=-1/8
[((-3)/2)^3 ]^2

Vận dụng
Biết vận tốc ánh sáng xấp xỉ bằng 299 792 458 m/s và ánh sáng Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất. Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
Giải
Ta có: 299792458 ≈ 300000000 = 3.10^8 (m/s)
Đổi 8 phút 19 giây = 499 giây ≈ 500 giây
Khoảng cách giữa Mặt Trời và Trái Đất là:
3.10^8.500=3.10^8.5.10^2=15.10^8 (km)
Hai mảnh vườn có dạng hình vuông. Mảnh vườn thứ nhất có độ dài cạnh là 19,5 m. Mảnh vườn thứ hai có độ dài cạnh là 6,5 m. Diện tích mảnh vườn thứ nhất gấp bao nhiêu lần diện tích mảnh vườn thứ hai?
Giải
Diện tích hình vuông thứ nhất là:
(19,5)^2 = 380,25 (m2)
Diện tích hình vuông thứ hai là:
(6,5)^2 = 42,25 (m2)
Ta có: 380,25 : 42,25=9380,25 :42,5= 9
⇒ Diện tích mảnh vườn thứ nhất gấp 9 lần diện tích mảnh vườn thứ hai.
a) (3,147)^3≈31,167
b) (-23,457)^5≈-7101700,278
c) (4/(-5))^4=256/625
d) (0,12)^2.((-13)/28)^5≈-3,107.10^(-4)
Câu hỏi 1: Tính: ((-1)/2)^5=?
A. 1/32
B. 1/10
C. (-1)/32
D. (-1)/10
Câu hỏi 2: Lũy thừa với số mũ lẻ của một số hữu tỉ âm mang dấu:
A. Dương
B. Âm
C. Âm khi số mũ âm
D. Không xác định
Câu hỏi 3: Tính nhanh
M=(100-1). (100- 22). (100- 32)…(100-502)
A. 0
B. 100
C. Không xác định
D. Đáp án khác
Câu hỏi 4: Kết quả của phép tính (2/5+1/2)^2là:
A. 9/10
B. 81/100
C. 41/100
D. Kết quả khác
Câu hỏi 5: Kết quả của phép tính (3/5)^15 〖.(0,36) 〗^5là:
A. 125/27
B. 25/127
C. 3125/243
D. 243/3125
HƯỚNG DẪN VỀ NHÀ
Ôn lại kiến thức đã học trong bài
Hoàn thành các bài tập còn lại trong SGK và SBT
Chuẩn bị bài mới “Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc”.
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!