Tải giáo án Powerpoint Toán 7 Cánh diều Chương 2 Bài 1. Số vô tỉ. Căn bậc hai số học

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC

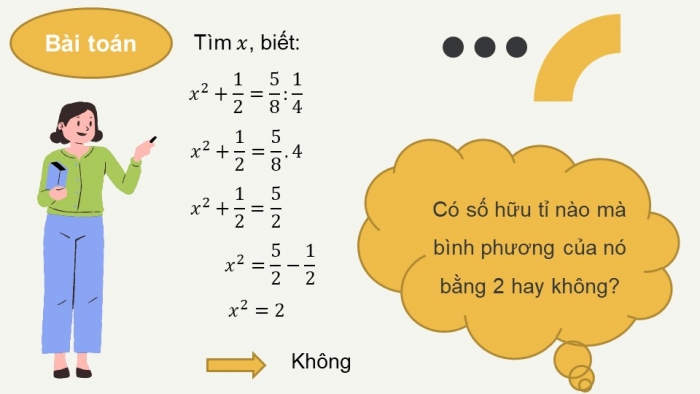
Bài toán

Tìm , biết:

BÀI 1: SỐ VÔ TỈ. CĂN BẬC HAI SỐ HỌC

NỘI DUNG BÀI HỌC

Số vô tỉ

Căn bậc hai số học

Luyện tập

1. SỐ VÔ TỈ
2. Khái niệm số vô tỉ

Số vô tỉ là các số không phải là số hữu tỉ.

VD:

Cách tính, lịch sử hình thành số Pi?

2. Số thập phân vô hạn không tuần hoàn

Viết số hữu tỉ  dưới dạng số thập phân vô hạn tuần hoàn.

Những số thập phân vô hạn mà phần thập phân của chúng không có một chu kì nào cả được gọi là số thập phân vô hạn không tuần hoàn.

VD:

3. Biểu diễn thập phân của số vô tỉ

Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.

Ví dụ 1

Các phát biểu sau đúng hay sai? Vì sao?

1. a) Nếu thì a không thể là số vô tỉ.
2. b) Nếu thì a không thể là số vô tỉ.
3. c) Số thập phân hữu hạn là số vô tỉ.

Giải

1. a) Đúng. Ta có thể giải thích như sau: Nếu thì a là số hữu tỉ và do đó a được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn, tức là a không thể là số vô tỉ.
2. b) Đúng. Ta có thể giải thích như sau: Nếu a là số nguyên thì a cũng là số hữu tỉ và do đó theo lập luận trên a không thể là số vô tỉ.
3. c) Sai. Ta có thể giải thích như sau: Số thập phân hữu hạn không thể là số thập phân vô hạn không tuần hoàn và do đó không thể là số vô tỉ.

Luyện tập 1

Phát biểu “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?

Khẳng định đúng vì những số không phải số hữu tỉ là số vô tỉ.

1. CĂN BẬC HAI SỐ HỌC

Tính

 là căn bậc hai số học của

 là căn bậc hai số học của

• Khái niệm

Căn bậc hai số học của số  không âm là số  sao cho .

Căn bậc hai số học của một số không âm phải là số không âm.

Ví dụ:

nhưng không được gọi là căn bậc hai số học của .

Chú ý:

• Căn bậc hai số học của số được kí hiệu là .

• Căn bậc hai số học của số là số , viết là .

Lưu ý: Cho . Khi đó:

• Đẳng thức là đúng nếu và .
• .

Ví dụ 2

Chứng tỏ rằng:

1. a) Số là căn bậc hai số học của số
2. b) Số không phải căn bậc hai số học của

Giải

1. a) Ta có: và nên  là căn bậc hai số học của
2. b) Tuy nhưng nên  không phải là căn bậc hai số học của .

Ví dụ 3

Tìm giá trị của:

Nhận xét: Người ta chứng minh được rằng "Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì  là số vô tỉ." Như  vậy các số, , , , ... đều là số vô tỉ.

Luyện tập 2

Tìm giá trị của:

Sử dụng máy tính cầm tay

Ví dụ 4

Dùng máy tính cầm tay để tính giá trị trong mỗi trường hợp sau:

III. LUYỆN TẬP

1. a) Đọc các số sau:

đọc là: căn bậc hai số học của mười lăm

 đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu

 đọc là: căn bậc hai số học của không phẩy tám mươi hai

1. b) Viết các số sau:

Căn bậc hai số học của  viết là: 

Căn bậc hai số học của   viết là: 

Căn bậc hai số học của   viết là: 

Chứng tỏ rằng:

1. a) Số là căn bậc hai số học của
2. b) Số không phải là căn bậc hai số học của
3. c) Số là căn bậc hai số học của số nhưng không phải là căn bậc hai số học của số  

Giải

1. a) Vì và  nên số là căn bậc hai số học của số .
2. b) Vì tuy  nhưng nên số không phải là căn bậc hai số học của số .
3. c) Vì  và nên số là căn bậc hai số học của số . Ngược lại, vì nên không phải là căn bậc hai số học của số .

Tính giá trị của biểu thức:

1. a)
2. b)
3. c)
4. d)

Vận dụng

Tìm số thích hợp điền vào

Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.

1. a) Tính diện tích của hình vuông ABCD
2. b) Tính độ dài đường chéo AB.

Giải

1. a) Diện tích của hình vuông ABCD là:
2. b) Độ dài đường chéo AB là:

Ghi nhớ:  là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1.

Phát biểu nào sau đây là sai ?

Số nào trong các số sau không là số hữu tỉ?

Trong các số sau đây số nào là số vô tỉ?

Căn bậc hai số học của 225 là:

Chọn câu trả lời sai. Nếu thì  bằng:

Nếu thì  bằng:

3. 27
4. 9

Trong các số  số nào không có căn bậc hai là số hữu tỉ.

HƯỚNG DẪN VỀ NHÀ

1. Ôn lại kiến thức đã học trong bài
2. Hoàn thành các bài tập trong SBT
3. Chuẩn bị bài mới “Tập hợp R các số thực”.

CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!