Tải giáo án Powerpoint Toán 7 Cánh diều Chương 2 Bài 2. Tập hợp R các số thực

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC

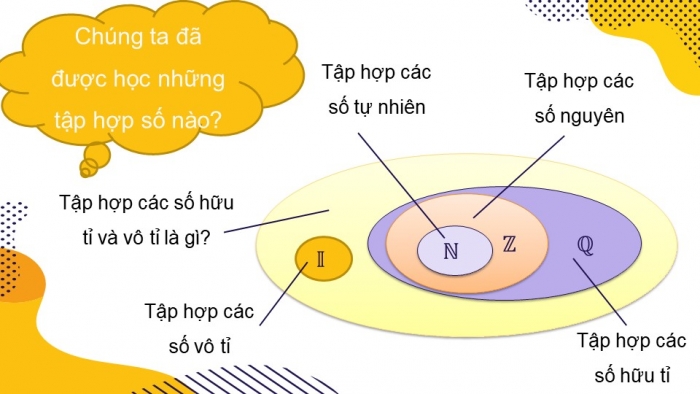
Chúng ta đã được học những tập hợp số nào?

Tập hợp các số tự nhiên

Tập hợp các số nguyên

Tập hợp các số hữu tỉ

Tập hợp các số hữu tỉ và vô tỉ là gì?

Tập hợp các số vô tỉ

BÀI 2: TẬP HỢP  CÁC SỐ THỰC (3 tiết)

NỘI DUNG BÀI HỌC

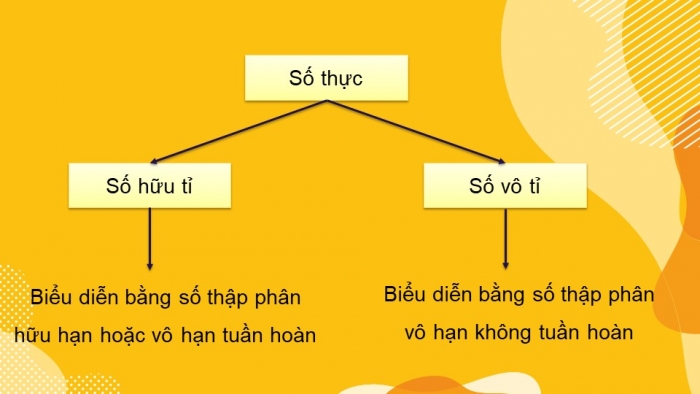
Số thực

Biểu diễn số thực trên trục số

Số đối của một số thực

So sánh các số thực

1. SỐ THỰC
2. Tập hợp số thực

HĐ1

1. a) Hai ví dụ về số hữu tỉ:
2. b) Hai ví dụ về số hữu tỉ:

• Khái niệm:

Số hữu tỉ và số vô tỉ được gọi chung là số thực. Tập hợp các số thực kí hiệu là .

là các số thực.

2. Biểu diễn thập phân của số thực
3. a) Nêu biểu diễn thập phân của số hữu tỉ.
4. b) Nêu biểu diễn thập phân của số vô tỉ.

Giải:

1. a) Số hữu tỉ được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
2. a) Số hữu tỉ được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
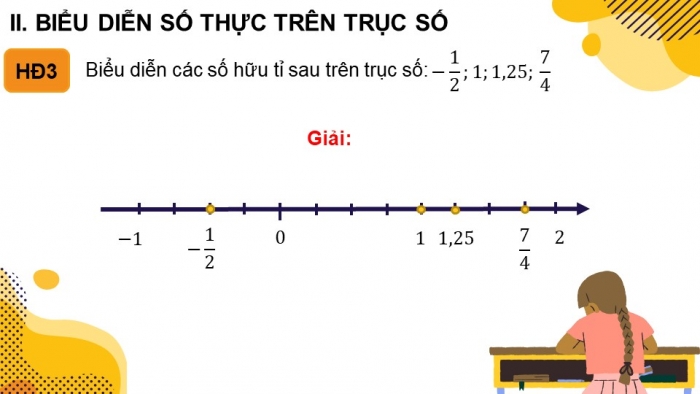
3. BIỂU DIỄN SỐ THỰC TRÊN TRỤC SỐ

Biểu diễn các số hữu tỉ sau trên trục số:

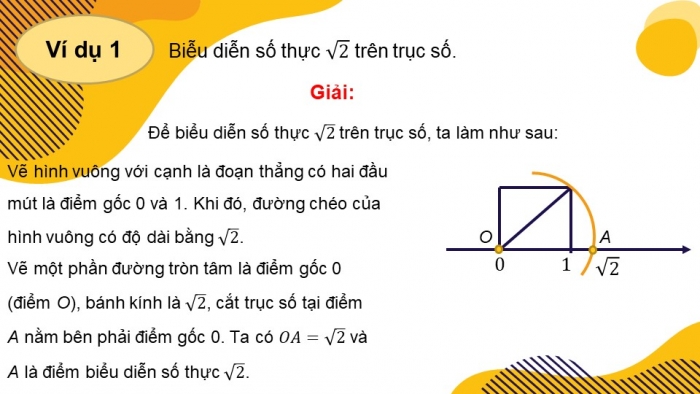
Ví dụ 1

Biễu diễn số thực  trên trục số.

Giải:

Để biểu diễn số thực trên trục số, ta làm như sau:

Vẽ hình vuông với cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và 1. Khi đó, đường chéo của hình vuông có độ dài bằng .

Vẽ một phần đường tròn tâm là điểm gốc 0 (điểm O), bánh kính là , cắt trục số tại điểm A nằm bên phải điểm gốc 0. Ta có    và A là điểm biểu diễn số thực .

Nhận xét

+ Do  không phải là số hữu tỉ mà là số vô tỉ nên không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

+ Người ta chứng minh được rằng: Mỗi số thực đều được biểu diễn bởi một điểm trên trục số; ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực. Vì thế, trục số còn được gọi là trục số thực.

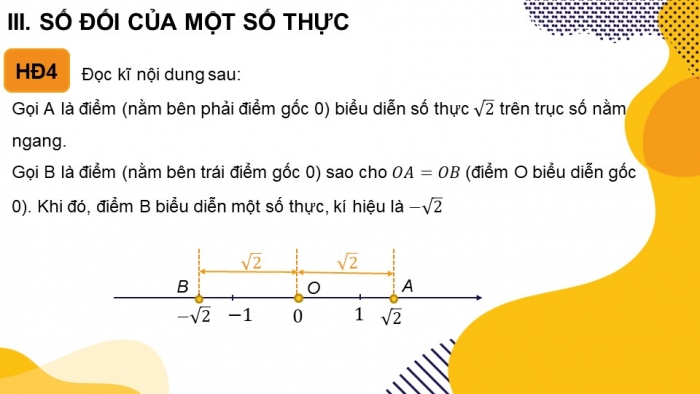
III. SỐ ĐỐI CỦA MỘT SỐ THỰC

          Đọc kĩ nội dung sau:

Gọi A là điểm (nằm bên phải điểm gốc 0) biểu diễn số thực  trên trục số nằm ngang.

Gọi B là điểm (nằm bên trái điểm gốc 0) sao cho (điểm O biểu diễn gốc 0). Khi đó, điểm B biểu diễn một số thực, kí hiệu là

Kết luận

• Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc và cách đều điểm gốc  được gọi là hai số đối nhau.
• Số đối của số thực kí hiệu là .
• Số đối của là .

Nhận xét: Số đối của số  là số , tức là .

Ví dụ 2

Tìm số đối của mỗi số sau:

Số đối của       là:

Số đối của  là:

Số đối của  là:

Luyện tập 1

Tìm số đối của mỗi số sau:

Số đối của       là:

Số đối của  là:

Số đối của  là:

1. SO SÁNH CÁC SỐ THỰC
2. So sánh hai số thực

• Nếu số thực nhỏ hơn số thực  thì ta viết hay .
• Số thực lớn hơn gọi là số thực dương.
• Số thực nhỏ hơn gọi là số thực âm.
• Số 0 không phải là số thực dương, cũng không phải là số thực âm.
• Nếu và thì .

2. Cách so sánh hai số thực
3. a) So sánh hai số thập phân sau: và
4. b) Nêu quy tắc so sánh hai số thập phân hữu hạn.

Giải:

1. a) Vì nên
2. b) Quy tắc so sánh hai số thập phân hữu hạn:

+ So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương

+ So sánh 2 số thập phân dương:

• Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
• Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

+ So sánh 2 số thập phân âm: Nếu thì

Ví dụ 3

So sánh:

1. a) và
2. b) và

Giải:

1. a) Do nên
2. b) Do nên

Luyện tập 2

So sánh hai số thực sau:

1. a) và

Ta có:

Mà

1. b) và

Ta có:

Mà

hay

Chú ý

Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc sau: Với a, b là hai số thực dương, nếu a > b thì   > .

3. Minh hoạ trên trục số

Giả sử hai điểm lần lượt biểu diễn hai số thực trên trục số nằm ngang. Ta thừa nhận nhận xét sau:

• Nếu hay thì điểm nằm bên trái điểm ;
• Ngược lại, nếu điểm x nằm bên trái điểm thì hay .

Đối với hai điểm lần lượt biểu diễn hai số thực trên trục số thẳng đứng, ta cũng thừa nhân nhận xét sau:

• Nếu hay thì điểm nằm dưới điểm ;
• Ngược lại, nếu điểm nằm phía dưới điểm  thì hay .

Ví dụ 4

1. a) Sắp xếp các số sau theo thứ tự tăng dần:
2. b) Trong ba điểm A, B, C trên trục số sau có một điểm biểu diễn số thực . Hãy xác định điểm đó.

Giải:

1. a) Ta có: và nên

Do  nên  hay

Vậy cá số đã cho được sắp xếp theo thứ tự tăng dần là:  

1. b) Do nên điểm nằm bên phải điểm -1 và nằm bên trái điểm 3 trên trục số nằm ngang  Điểm B

LUYỆN TẬP

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

1. a) Nếu thì

Đúng vì một số nguyên cũng là số thực.

1. b) Nếu thì

Đúng vì một số hữu tỉ cũng là số thực.

1. c) Nếu thì

Sai vì một số thực có thể không là số nguyên.

1. d) Nếu thì

Sai vì một số thực có thể là số hữu tỉ hoặc không là số hữu tỉ.

Tìm số đối của mỗi số sau:

So sánh:

1. a) và

Ta có:

Mà:

hay

1. b) và

Mà: 

VẬN DỤNG

Tìm chữ số thích hợp cho

1. a)
2. b)
3. c)
4. d)
5. a) Sắp xếp các số sau theo thứ tự tăng dần

Giải:

Ta có:

Vì

Mà nên

 Thứ tự sắp xếp là:

1. b) Sắp xếp các số sau theo thứ tự giảm dần

Giải:

Ta có:

;

Ta có:

Ta được:

Nên

 Thứ tự sắp xếp là:

Câu 1. Phát biểu nào sau đây là đúng?

1. Số nguyên không phải số thực
2. Phân số không phải số thực
3. Số vô tỉ không phải số thực
4. Cả ba loại số trên đều là số thực

Câu 2.  Phát biểu nào sau đây sai?

1. Mọi số vô tỉ đều là số thực
2. Mọi số thực đều là số vô tỉ.
3. Mọi số nguyên đều là số hữu tỉ
4. Số 0 là số hữu tỉ cũng là số thực.

Câu 3. Chọn chữ số thích hợp điền vào chỗ trống

1. 1 ; 2; ...9
2. 3
4. 0; 1

Câu 4. Chọn khẳng định sai trong các khẳng định sau:

1. ; ;  là các số thực
2. là các số thực
3. Số 0 vừa là số hữu tỉ vừa là số vô tỉ
4. 1; 2; 3; 4 là các số thực

Câu 5. Số đối của các số  lần lượt là

HƯỚNG DẪN VỀ NHÀ

Ôn lại kiến thức đã học trong bài

Hoàn thành các bài tập SBT

Chuẩn bị bài mới “Bài 3. Giá trị tuyệt đối của một số thực”

CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!