Tải giáo án Powerpoint Toán 7 KNTT bài 11: Định lí và chứng minh định lí (1 tiết)
Rõ nét về file powerpoint trình chiếu. => Xem thêm
CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC MỚI!
Trong Bài 10, ta dùng cách đo đạc để kiểm nghiệm tính chất sau:
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”.
Tuy nhiên, đo đạc chỉ cho kết quả gần đúng và trong trường hợp cụ thể.
Vậy có cách nào khác để chắc chắn tính chất đúng cho mọi trường hợp không?
BÀI 10: ĐỊNH LÍ VÀ CHỨNG MINH ĐỊNH LÍ (1 Tiết)
Định lí. Giả thiết và kết luận của định lí
“Nếu hai góc đối đỉnh thì bằng nhau”, được suy ra từ một điều đúng đã biết là “hai góc kề bù có tổng số đo bằng 180 ”.
Nếu hai góc đối đỉnh thì bằng nhau
KẾT LUẬN
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:
Nếu .... thì .....
- Phần giữa từ “nếu ” và từ “thì” là giả thiết của định lí.
- Phần sau từ “thì” là kết luận của định lí.
Ví dụ
Trong định lí “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại” thì có:
Giả thiết là “một đường thẳng vuông góc với một trong hai đường thẳng song song”;
Kết luận là “nó cũng vuông góc với đường thẳng còn lại”.
Ta có thể viết giả thiết, kết luận trên bằng kí hiệu như sau:
Luyện tập 1
Vẽ hình và viết giả thiết, kết luận của định lí:
“Hai góc đối đỉnh thì bằng nhau”
Giả thiết: hai góc đối đỉnh.
Kết luận: bằng nhau.
Thế nào là chứng minh định lí?
Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.
|
GT |
a // b, c cắt a tại A, c cắt b tại B; , là hai góc đồng vị. |
|
KL |
= . |
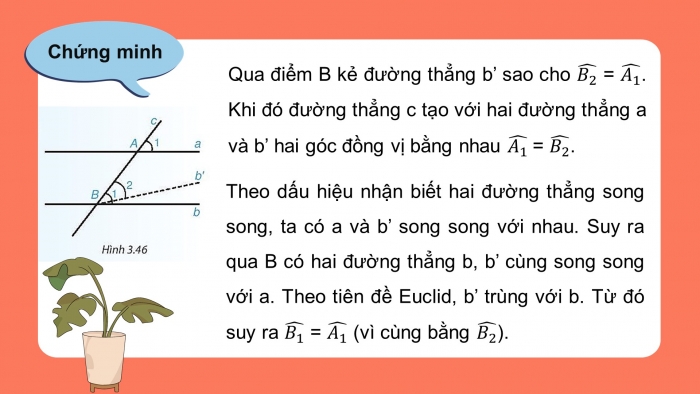
Chứng minh
Qua điểm B kẻ đường thẳng b’ sao cho = . Khi đó đường thẳng c tạo với hai đường thẳng a và b’ hai góc đồng vị bằng nhau = .
Theo dấu hiệu nhận biết hai đường thẳng song song, ta có a và b’ song song với nhau. Suy ra qua B có hai đường thẳng b, b’ cùng song song với a. Theo tiên đề Euclid, b’ trùng với b. Từ đó suy ra = (vì cùng bằng ).
Luyện tập 2
Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.
|
GT |
là hai góc kề bù, . |
|
KL |
Giải
Ta có: (hai góc kề bù)
Mà
.
Tranh luận
Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?
Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?
Hai góc bằng nhau chưa chắc đã đối đỉnh.
Ví dụ: Hai góc vuông mà kề bù bằng nhau và đều bằng nhưng không đối đỉnh.
LUYỆN TẬP
Bài 3.24 (SGK - tr57)
Có thể coi định lí: “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Giải
Nếu d’ và d’’ phân biệt, cùng vuông góc với d thì d cắt d’, d’’ tạo thành 8 góc vuông. Do hai góc vuông nào cũng bằng nhau nên theo dấu hiệu góc đồng vị bằng nhau thì hai đường thẳng d’ và d’’ song song.
Bài 3.24 (SGK - tr57)
Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó, ta đã sử dụng những điều đúng đã biết nào?
Giải
- Nếu d không cắt d’’ thì d song song với d’’ nên qua giao điểm A của d và d’ có hai đường thẳng là d và d’ cùng song song với d’’. Theo tiên đề Euclid, d phải trùng với d’, trong khi theo giả thiết thì d khác d’ vì vuông góc với d’.
Vậy d phải cắt d’’ tại một điểm B.
- d cắt d’, d’’ tạo thành 8 góc, trong đó 4 góc tại A đều vuông. Từ tính chất của hai đường thẳng song song khi d cắt hai đường thẳng song song d’, d’’ thì hai góc đồng vị bằng nhau nên trong bốn góc còn lại tại B có một góc vuông.
Vậy d vuông góc với d’’.
Bài 3.26 (SGK - tr57)
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây là đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì = .
(2) Nếu tia Ot thỏa mãn = thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.
(Gợi ý: Xét tia đối của một tia phân giác)
Giải
(1) đúng vì điều đó nằm trong tính chất của tia phân giác.
(2) không đúng vì nếu lấy tia đối Ot’ của tia phân giác Ot của góc xOy thì do kề bù với kề bù với , ta có , nhưng Ot’ không là tia phân giác của góc xOy.
Câu 1:
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia”.
Câu 2: Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng.
Câu 3: Điền dấu X vào ô thích hợp
HƯỚNG DẪN VỀ NHÀ
Ghi nhớ các kiến thức đã học
Hoàn thành bài tập trong SBT
Chuẩn bị bài “Luyện tập chung”
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!
Hình ảnh về file sile, ppt trình chiếu











.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Giáo án Powerpoint Toán 7 Kết nối, giáo án điện tử Toán 7 KNTT bài 11: Định lí và chứng minh định, giáo án trình chiếu Toán 7 kết nối bài 11: Định lí và chứng minh định
