Tải giáo án Powerpoint Toán 7 KNTT bài 2: Cộng, trừ, nhân, chia số hữu tỉ (2 tiết)

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!
Giả sử một khinh khí cầu bay lên từ mặt đất theo chiều thẳng đứng với vận tốc 0,8 m/s trong 50 giây. Sau đó nó giảm dần độ cao với vận tốc 5/9 m/s. Hỏi sau 27 giây kể từ khi hạ độ cao, khinh khí cầu cách mặt đất bao nhiêu mét?
Gợi ý:
Trong 50s đầu, với vận tốc 0,8 m/s, khinh khí cầu bay lên một quãng đường cách mặt đất bao xa?
Sau 27s, với vận tốc 5/9 m/s, khinh khí cầu giảm độ cao bao nhiêu?
Sau 27s, khinh khí cầu cách mặt đất bao xa?
BÀI 2: CỘNG, TRỪ, NHÂN, CHIA SỐ HỮU TỈ (2 Tiết)
NỘI DUNG BÀI HỌC
Cộng và trừ hai số hữu tỉ
Nhân và chia hai số hữu tỉ
1. Cộng và trừ hai số hữu tỉ
Thảo luận nhóm thực hiện HĐ1 và HĐ2 để ôn lại quy tắc và cách cộng, trừ phân số (cùng mẫu, khác mẫu).
Nhắc lại quy tắc cộng và trừ hai phân số rồi thực hiện phép tính:
a) (-7)/8 + 5/12
b) (-5)/7 - 8/21
Quy tắc cộng hai phân số:
Cùng mẫu:
Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.
Muốn trừ hai phân số có cùng mẫu số, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu.
Khác mẫu:
Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng, sau đó cộng hai phân số có cùng mẫu.
Muốn trừ hai phân số khác mẫu, ta quy đồng mẫu hai phân số rồi trừ hai phân số đó.
Thực hiện phép tính:
a) (-7)/8 + 5/12 = (-21)/24 + 10/24 = (-11)/24
b) (-5)/7 - 8/21 = (-15)/21 - 8/21 = (-23)/21
HĐ2
Viết các hỗn số và số thập phân trong phép tính sau dưới dạng phân số rồi thực hiện phép tính:
a) 0,25 + 15/12 = 1/4 + 17/12 = 3/12 + 17/12 = 20/12 = 5/3
b) -1,4 - 3/5 = - 14/10 - 3/5 = - 14/10 - 6/10 = (-20)/10 = -2
Vậy muốn cộng trừ hai số hữu tỉ, ta làm như thế nào?
Ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
Ví dụ 1: Tính
a) 2/(-3) + 2,5 + 1/3 + 11/2 = (-2)/3 + 5/2 + 1/3 + 3/2
Viết số hữu tỉ dưới dạng phân số có mẫu dương
= (-2)/3 + 1/3 + 5/2 + 3/2
Tính chất giao hoán
= ((-2)/3+1/3) + (5/2+3/2)
Tính chất kết hợp
= (-1)/3 + 4 = 11/3
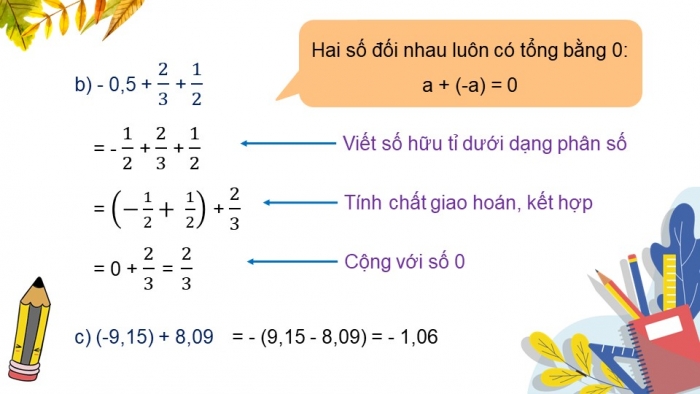
b) - 0,5 + 2/3 + 1/2
Hai số đối nhau luôn có tổng bằng 0:
a + (-a) = 0
= - 1/2 + 2/3 + 1/2 Viết số hữu tỉ dưới dạng phân số
= (-1/2+ 1/2) + 2/3 Tính chất giao hoán, kết hợp
= 0 + 2/3 = 2/3 Cộng với số 0
c) (-9,15) + 8,09 = - (9,15 - 8,09) = - 1,06
Chú ý:
Phép cộng số hữu tỉ cũng có tính chất giao hoán, kết hợp giống phép cộng phân số.
Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta áp dụng quy tắc cộng và trừ đối với số thập phân.
Luyện tập 1: Tính
a) - 7 - (-5/8) = - 56/8 + 5/8 = - 51/8
b) - 21,25 + 13,3 = - (21,25 - 13, 3) = - 7,95
Nhận xét:
Trong tập các số hữu tỉ Q, ta cũng có quy tắc dấu ngoặc tương tự như trong tập các số nguyên Z.
Ví dụ 2: Tính
8/9 - [7/4 - (3/4-2/3)]
= 8/9 - 7/4 + (3/4-2/3)
= 8/9 - 7/4 + 3/4 - 2/3
= (8/9-2/3) - (7/4-3/4)
= (8/9-6/9) - 1 = 2/9 - 1 = - 7/9
Chú ý:
Đối với một tổng trong Q, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong Z.
Luyện tập 2: Bỏ dấu ngoặc rồi tính các tổng sau
a) 9/10 - (6/5-7/4)
= 9/10 - 6/5 + 7/4 = 18/20 - 24/20 + 35/20 = 29/20
b) 6,5 + [0,75 - (8,25 - 1,75)]
= 6,5 + 0,75 - 8,25 + 1,75 = 0,75
Vận dụng 1:
Khoai tây là thức ăn chính của người châu Âu và là món ăn ưa thích của người Việt Nam. Trong 100 gam khoai tây khô có 11 gam nước; 6,6 gam protein; 0,3 gam chất béo; 75,1 gam glucid và các chất khác. Em hãy cho biết khối lượng của các chất khác trong 100 gam khoai tây khô.
Khối lượng các chất khác trong 100g khoai tây khô là:
100 – (11 + 6,6 + 0,3 + 75,1) = 7 (g)
2. Nhân và chia hai số hữu tỉ
Cách nhân và chia hai số hữu tỉ
Hoạt động nhóm thực hiện HĐ3.
HĐ3
Viết các hỗn số và số thập phân trong phép tính sau dưới dạng phân số rồi thực hiện phép tính:
a) 0,36. (-5)/9 = 9/25 . (-5)/9 = (-1)/5
b) (-7)/6 : 15/7 = (-7)/6 : 12/7 = (-7)/6 . 7/12 = (-49)/72
Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
Ví dụ 3:
a) 6/7 . 0,25 = 6/7 . 1/4 = 6/28 = 3/14
b) - 2,4 : 6/5 = (-24)/10 : 6/5 = (-12)/5 . 5/6 = - 2
Luyện tập 3: Tính
a) ((-9)/13) . ((-4)/5) = 36/65
b) - 0,7 : 3/2 = (-7)/10: 3/2=(-7)/10 . 2/3 = (-7)/15
Luyện tập 4: Tính một cách hợp lí
7/6. 31/4 + 7/6. (- 0,25) = 7/6. 13/4 + 7/6. (-1)/4
= 7/6. (13/4-1/4) = 7/6. 12/4 = 7/6 . 3 = 7/2
Chú ý:
Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.
1,25. (- 4,6) = - (1,25. 4,6) = - 5,75
7,8 : (- 0,13) = - (7,8 : 0,13) = - 60.
Vận dụng quy tắc tính toán với số hữu tỉ để làm ví dụ mở đầu để hoàn thành Ví dụ 4 và so sánh lại với lời giải đã có trong sách.
Trong 50s đầu, khinh khí cầu bay lên cách mặt đất là: 0,8. 50 = 40 (m)
Sau 27s, khinh khí cầu giảm độ cao là: 5/9. 27 = 15 (m)
Vậy sau 27s, khinh khí cầu cách mặt đất là: 40 - 15 = 25 (m)
Vận dụng 2
Cho hai tấm ảnh có cùng kích thước 10 cm x 15 cm được in trên giấy ảnh kích thước 21,6 cm x 27,9 cm như Hình 1.8. Nếu cắt ảnh theo đúng kích thước thì diện tích phần giấy ảnh còn lại là bao nhiêu?
Diện tích 1 tấm ảnh là: 10.15 = 150 (cm^2)
Diện tích tấm giấy là: 21,6 . 27,9 = 602,64 (cm^2)
Diện tích phần giấy ảnh còn lại là: 602,64 – 2.150 = 302,64 (cm^2)
LUYỆN TẬP
Bài 1.7 (SGK - tr13)
a) (-6)/18 + 18/27 = (-1)/3 + 2/3 = 1/3
b) 2,5 - (-6/9) = 5/2 + 6/9 = 5/2 + 2/3 = 15/6 + 4/6 = 19/6
c) - 0,32. (- 0,875)
d) (- 5) : 21/5 = (- 5) : 11/5 = - 25/11
Bài 1.8 (SGK - tr13)
Tính giá trị của các biểu thức sau:
a) (8+2 1/3-3/5) - (5 + 0,4) - (3 1/3-2)
= (8+ 7/3 - 3/5) - (5+2/5) - (10/3-2) = 8 + 7/3 - 3/5 - 5 - 2/5 - 10/3 + 2
= (8 - 5 + 2) + (7/3-10/3) - (3/5+2/5) = 5 - 1 - 1 = 3
b) (7 - 1/2 - 3/4) : (5 - 1/4- 5/8)
= (28/4-2/4-3/4) : (40/8-2/8-5/8)
= 23/4 : 33/8 = 23/4. 8/33 = 46/33
Bài 1.10 (SGK - tr13)
Tính một cách hợp lí:
0,65. 78 + 21/5 . 2 020 + 0,35. 78 - 2,2. 2 020
= 0,65. 78 + 2,2. 2 020 + 0,35. 78 - 2,2. 2020
= 78. (0,65 + 0,35) + 2 020.(2,2 - 2,2)
= 78. 1 + 2 020. 0 = 78
VẬN DỤNG
Bài 1.9 (SGK - tr13)
Em hãy tìm cách “nối” các số ở những chiếc lá trong Hình 1.9 bằng dấu các phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở bông hoa.
(-25 . 4) + [10 : (-2)] = -105
Bài 1.10 (SGK - tr13)
Ngăn đựng sách của một giá sách trong thư viện dài 120 cm. Người ta dự định xếp các cuốn sách dày khoảng 2,4 cm vào ngăn này. Hỏi ngăn sách này có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?
Giải
Ngăn sách đó có thể để được nhiều nhất số cuốn sách là: 120 : 2,4 = 50 (cuốn sách)
Câu 1: Nếu x = a/b, y = c/d thì x.y bằng
A. (a.c)/(b.d)
B. (a+c)/(b+d)
C. (a.d)/(b.c)
D. (a+d)/(b+c)
Câu 2: Kết quả của phép tính 9/5 : ((-3)/4)
A. 3/4
B. 2/15
C. (-12)/5
D. (-3)/4
Câu 3: Tìm x thỏa mãn x : (2/5 -1 2/5) = 1
A. x = -1
B. x = 1
C. x = 5/2
D. x = (-5)/2
Câu 4: Gọi x_0 là giá trị thỏa mãn 5/7 : x - 2/5 = 1/3.
Chọn đáp án đúng
A. x_0 = 1
B. x_0 > 1
C. x_0 = -1
D. x_0 < 1
Câu 5: So sánh A và B biết:
A = 4/5. 20/8.(-4/3) và B = (-2)/22.5/18.(-121/25)
A. A > B
B. A < B
C. A = B
D. A ≥ B
HƯỚNG DẪN VỀ NHÀ
Ôn lại kiến thức đã học
Hoàn thành bài tập còn lại trong SGK và bài tập trong SBT
Chuẩn bị bài sau “Luyện tập chung”
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!