Tải giáo án Powerpoint Toán 7 KNTT bài: Luyện tập chung trang 82

BÀI LUYỆN TẬP CHUNG TRANG 80 (2 TIẾT)

1. KHỞI ĐỘNG
2. Em hãy trình bày khái niệm đường trung tuyến; định lí sự đồng quy của ba đường trung tuyến; tính chất trọng tâm.
3. Em hãy trình bày khái niệm đường phân giác, định lí về sự đồng quy của ba đường phân giác.
4. Em hãy trình bày khái niệm đường trung trực, định lí về sự đồng quy của ba đường trung trực.
5. Em hãy trình bày khái niệm đường cao, định lí về sự đồng quy của ba đường cao.

1. NỘI DUNG BÀI HỌC

Các dạng toán:

Dạng 1: Chứng minh đường trung tuyến và sử dụng tính chất đồng quy của ba đường trung tuyến

Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau sử dụng tính chất đồng quy của ba đường phân giác.

Dạng 3: Chứng minh hai đoạn thẳng bằng nhau sử dụng tính chất đồng quy của ba đường trung trực.

Dạng 4: Chứng minh các đoạn thẳng bằng nhau, các đường thẳng vuông góc, các đường thẳng đồng quy sử dụng tính chất ba đường cao của tam giác.

Dạng 5: Chứng minh tam giác cân

III. PHẦN TRIỂN KHAI KIẾN THỨC

HĐ: PHÂN TÍCH CÁC VÍ DỤ:

GV giới thiệu các dạng toán HS cần nắm được:

Dạng 1: Chứng minh đường trung tuyến và sử dụng tính chất đồng quy của ba đường trung tuyến

Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau sử dụng tính chất đồng quy của ba đường phân giác.

Dạng 3: Chứng minh hai đoạn thẳng bằng nhau sử dụng tính chất đồng quy của ba đường trung trực.

Dạng 4: Chứng minh các đoạn thẳng bằng nhau, các đường thẳng vuông góc, các đường thẳng đồng quy sử dụng tính chất ba đường cao của tam giác.

Dạng 5: Chứng minh tam giác cân

HS đọc, nêu phương pháp giải, hoàn thành Ví dụ 1, trao đổi cặp đôi kiểm tra chéo

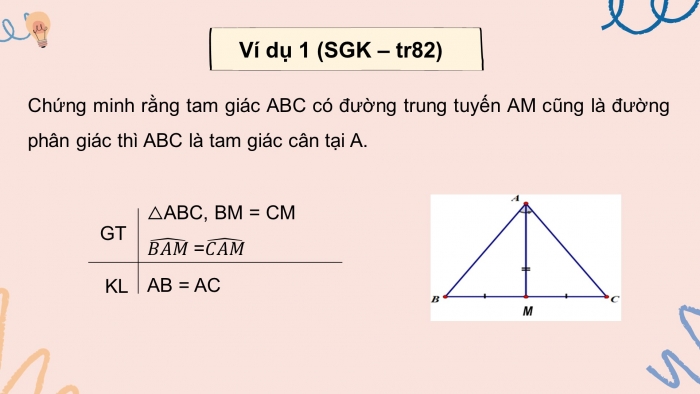
Ví dụ 1 (SGK-tr82): Chứng minh rằng tam giác ABC có đường trung tuyến AM cũng là đường phân giác thì ABC là tam giác cân tại A.

GV dẫn dắt đặt câu hỏi:

Các cách chứng minh một tam giác là tam giác cân?

Giải:

Chứng minh:

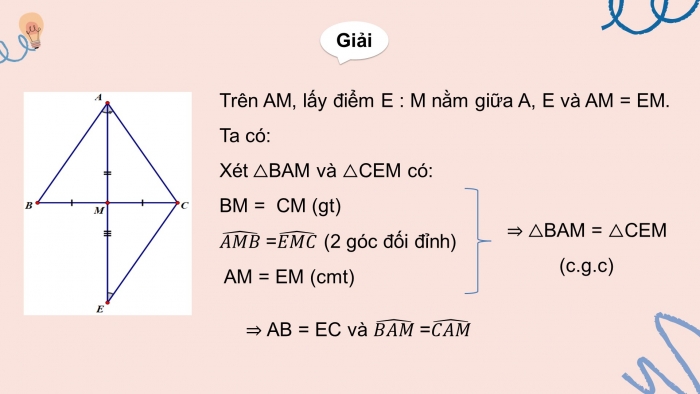
Trên AM, lấy điểm E : M nằm giữa A, E và AM = EM.

Ta có:

XétBAM và CEM có:

BM =  CM (gt)

= (2 góc đối đỉnh)

AM = EM (cd)

BAM = CEM (c.g.c),

AB = EC và =

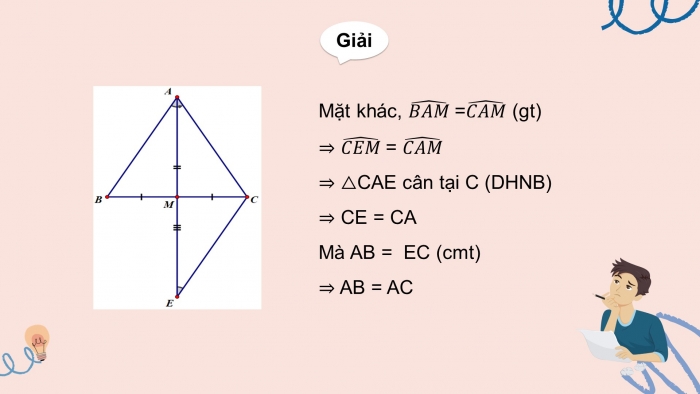
Mặt khác, = (gt),

 =

 CAE cân tại C (DHNB)

 CE = CA

Mà AB =  EC (cmt)

 AB = AC

HS đọc, tự trình bày Ví dụ 2, sau đó trao đổi nhóm đôi kiểm tra chéo.

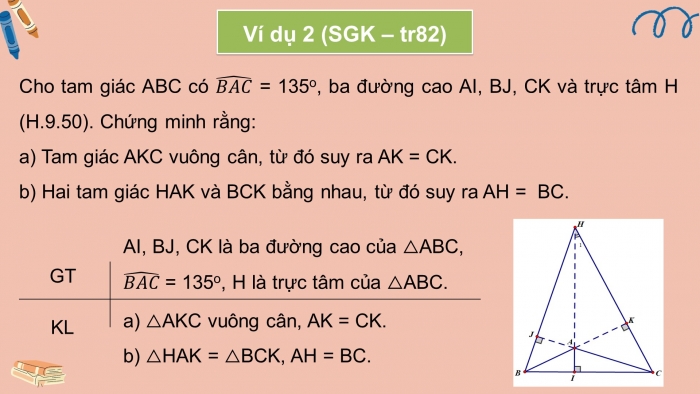
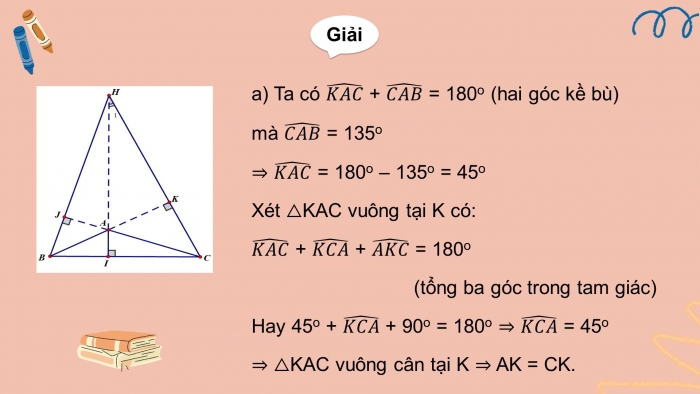
Ví dụ 2 (SGK-tr82): Cho tam giác ABC có  = 135^o, ba đường cao AI, BJ, CK và trực tâm H (H.9.50). Chứng minh rằng:

1. a) Tam giác AKC vuông cân, từ đó suy ra AK = CK.
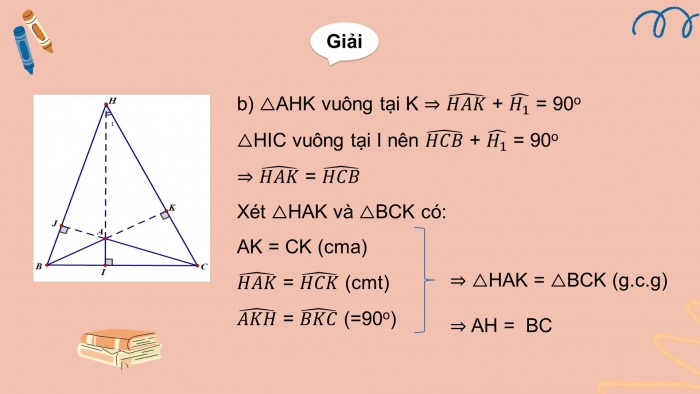
2. b) Hai tam giác HAK và BCK bằng nhau, từ đó suy ra AH =

Giải:

Hình ảnh:

Chứng minh:

1. a) Ta có + = 180^o (hai góc kề bù)

mà  = 135^o

  = 180^o – 135^o = 45^o

Xét KAC vuông tại K có: