Tải giáo án Powerpoint Toán 8 KNTT Bài 16: Đường trung bình của tam giác

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?

CHƯƠNG IV: ĐỊNH LÍ THALÈS

BÀI 16: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

Định nghĩa đường trung bình của tam giác

• Quan sát hình

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

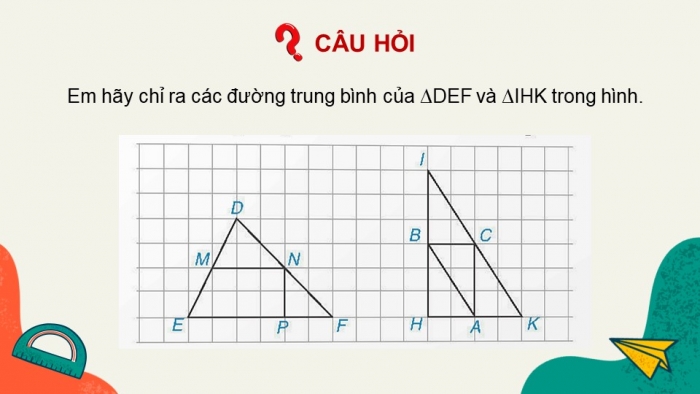
CÂU HỎI

Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong hình.

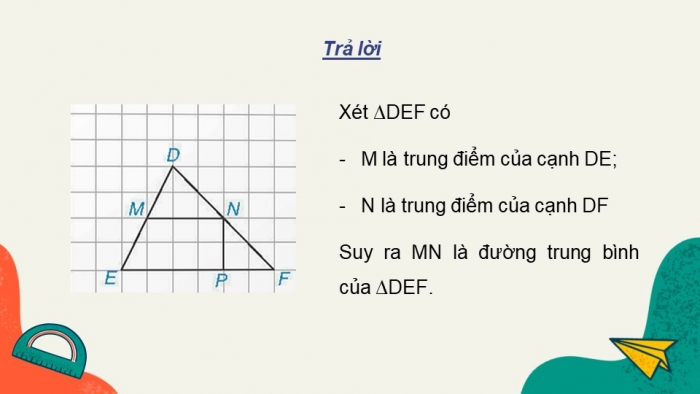
Trả lời

Xét ∆DEF có

• M là trung điểm của cạnh DE;
• N là trung điểm của cạnh DF

Suy ra MN là đường trung bình của ∆DEF.

Xét ∆IHK có:

• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK

Suy ra BC là đường trung bình của ∆IHK.

• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK

Suy ra AB là đường trung bình của ∆IHK.

• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK

Suy ra AC là đường trung bình của ∆DEF.

Vậy các đường trung bình của ∆IHK là AB, BC, AC.

Tính chất đường trung bình của tam giác

• Cho DE là đường trung bình của tam giác ABC. (H. 4.15)

HĐ 1:

Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.

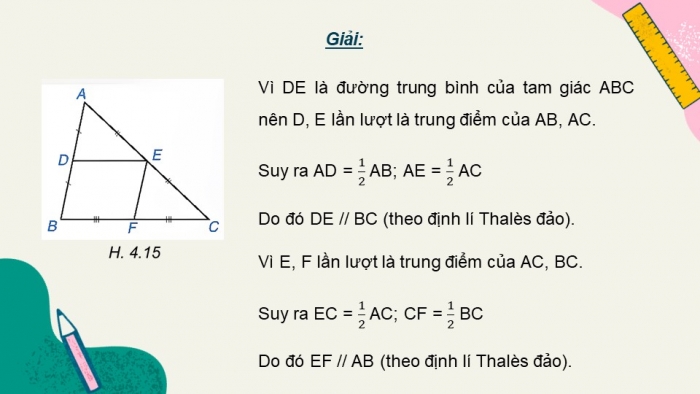
Giải:

Ta có AD = BD và D  AB nên D là trung điểm của AB

AE = EC và E  AC nên E là trung điểm của AC.

Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC.

Theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

• Cho DE là đường trung bình của tam giác ABC. (H. 4.15)

HĐ 2:

Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE =    BC.

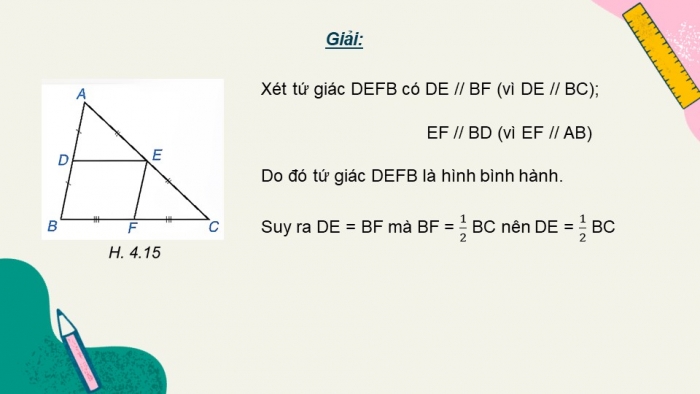
Giải:

Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB, AC.

Suy ra AD =  AB; AE =  AC

Do đó DE // BC (theo định lí Thalès đảo).

Vì E, F lần lượt là trung điểm của AC, BC.

Suy ra EC =  AC; CF =  BC

Do đó EF // AB (theo định lí Thalès đảo).

Xét tứ giác DEFB có DE // BF (vì DE // BC);

                                  EF // BD (vì EF // AB)

Do đó tứ giác DEFB là hình bình hành.

Suy ra DE = BF mà BF =  BC nên DE =  BC

ĐỊNH LÍ

Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.

Chú ý:       

Trong một tam giác, nếu một đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.

Ví dụ:

Cho tam giác ABC với M là trung điểm của AB, N là trung điểm của AC và BC = 10 cm. Tính MN.

Giải

Tam giác ABC có M là trung điểm của AB;

N là trung điểm của AC

Do đó, MN là đường trung bình của ABC

Suy ra MN =  BC = .10 = 5 (cm) (tính chất đường trung bình của tam giác)

Vậy MN = 5 cm.

LUYỆN TẬP

Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?

Giải

Tam giác ABC cân tại A nên 

Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.

  là hình thang.

Lại có  nên hình thang  là hình thang cân.

VẬN DỤNG

Em hãy trả lời câu hỏi trong tình huống mở đầu.

Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?

Giải

Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.

Suy ra DE là đường trung bình của    tam giác ABC.

Do đó DE =  BC 

Suy ra BC = 2DE = 2 . 500 = 1 000 (m)

Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

LUYỆN TẬP

TRÒ CHƠI TRẮC NGHIỆM