Tải giáo án Powerpoint Toán 8 KNTT Bài 33: Hai tam giác đồng dạng

NHIỆT LIỆT CHÀO MỪNG

CÁC EM ĐẾN VỚI BÀI HỌC MỚI!

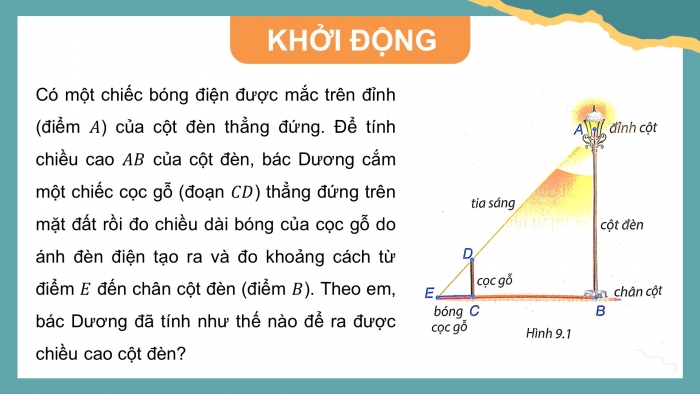
KHỞI ĐỘNG

Có một chiếc bóng điện được mắc trên đỉnh (điểm ) của cột đèn thẳng đứng. Để tính chiều cao  của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn ) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm  đến chân cột đèn (điểm ). Theo em, bác Dương đã tính như thế nào để ra được chiều cao cột đèn?

CHƯƠNG IX. TAM GIÁC ĐỒNG DẠNG

BÀI 33. HAI TAM GIÁC ĐỒNG DẠNG

NỘI DUNG BÀI HỌC

ĐỊNH NGHĨA

ĐỊNH LÍ

ĐỊNH NGHĨA

                 Trong hình 9.2,  và  

là hai tam giác có các cạnh tương ứng    song song và các góc   tương ứng bằng nhau, tức là  và

Nhìn hình vẽ, hãy cho biết giá trị các tỉ số sau

Qua sát hình ảnh ta thấy:  

KHÁI NIỆM

Tam giác  gọi là đồng dạng với tam giác  nếu:

Tam giác  đồng dạng với tam giác  được kí hiệu  (viết theo thứ tự cặp đỉnh tương ứng).

Tỉ số  được gọi là tỉ số đồng dạng của  với .

Nhận xét:

• Nếu  với tỉ số đồng dạng  thì  với tỉ số đồng dạng . Do vậy khi  thì ta nói hai tam giác  và  đồng dạng với nhau.
• Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng . Đặc biệt, mọi tam giác đồng dạng với chính nó.
• Nếu  với tỉ số đồng dạng  và  với tỉ số đồng dạng  thì  với tỉ số đồng dạng .

Ví dụ 1

Cho  và  là hai tam giác đều có

Chứng minh rằng  và tìm tỉ số đồng dạng.

Giải

Ta có  và .

Do vậy hai tam giác  và  có:

Vậy  với tỉ số đồng dạng

Luyện tập 1

Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.

Giải:

Ta thấy  với tỉ số đồng dạng .

Hoặc:  với tỉ số đồng dạng .

THỬ THÁCH NHỎ

Cho  . Chứng minh rằng:

1. a) Nếu tam giác cân tại thì tam giác  cân tại đỉnh
2. b) Nếu tam giác đều thì tam giác đều;
3. c) Nếu thì 
4. a) Vì và

    Nếu  cân tại     

       cân tại

Giải

b)

       đều.

1. c) Giả sử với hệ số đồng dạng .

    Suy ra:

ĐỊNH LÍ

HĐ2

Cho tam giác  và các điểm lần lượt nằm trên các cạnh sao cho  song song với  như Hình 9.4.

• Hãy viết các cặp góc bằng nhau của hai tam giác và giải thích vì sao chúng bằng nhau.
• Kẻ đường thẳng đi qua song song với  và cắt  tại . Hãy chứng tỏ  và suy ra 
• Tam giác và tam giác  có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng.

• Vì  (giả thiết)

Xét  và  có:

 chung, tức là:  (1)

 ;  (đồng vị) (2)

• Ta có ;  (giả thiết)

 là hình bình hành .

• Từ (1)(2)(3) suy ra .
• Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Chú ý:

Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác. Chẳng hạn, trong Hình 9.6 có . Khi đó, .

Ví dụ 2

Cho Hình 9.7, trong đó lần lượt là trung điểm của

lần lượt là trung điểm của . Hãy liệt kê tất cả các cặp tam giác (phân biệt) đồng dạng.

Giải

Tam giác  có  lần lượt là trung điểm của nên  là đường trung bình của tam giác .

Suy ra . (1)

Do đó  (theo định lí trên).

Tương tự,  là đường trung bình của tam giác nên . (2)