Tải giáo án Powerpoint Toán 8 KNTT bài: Luyện tập chung chương III (1 tiết)
Tải bài giảng điện tử powerpoint Toán 8 kết nối tri thức bài: Luyện tập chung chương III (1 tiết). Bài học được thiết kể đẹp mắt, nội dung giảng dạy hay nhiều trò chơi và video phong phú thu hút học sinh tập trung nắm bắt kiến thức quan trong. Giáo án tải về chỉnh sửa được. Kéo xuống để xem chi tiết
Rõ nét về file powerpoint trình chiếu. => Xem thêm
CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY!
KHỞI ĐỘNG
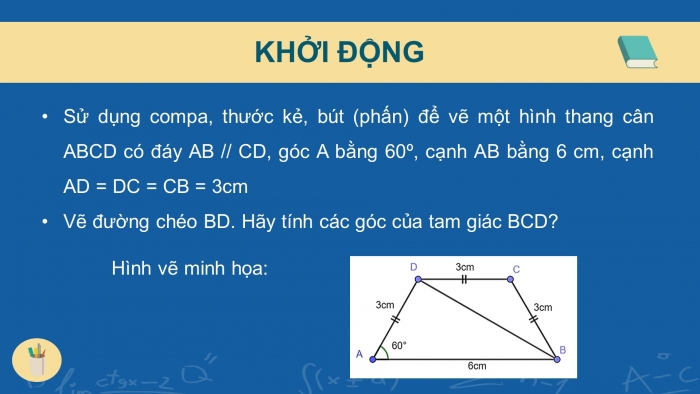
- Sử dụng compa, thước kẻ, bút (phấn) để vẽ một hình thang cân ABCD có đáy AB // CD, góc A bằng 60º, cạnh AB bằng 6 cm, cạnh AD = DC = CB = 3cm
- Vẽ đường chéo BD. Hãy tính các góc của tam giác BCD?
Hình vẽ minh họa:
CHƯƠNG III. TỨ GIÁC
LUYỆN TẬP CHUNG
Ví dụ 1 (SGK – tr56)
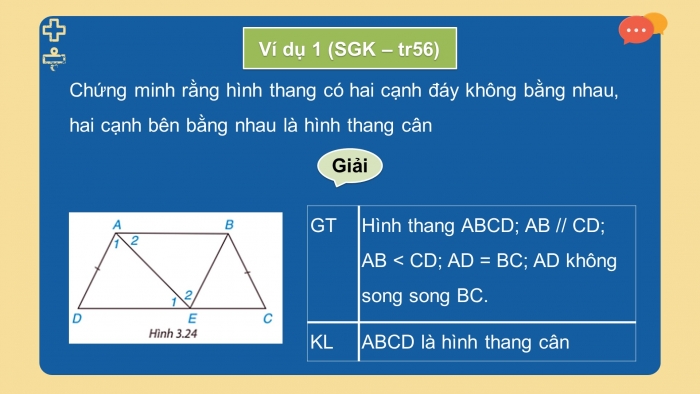
Chứng minh rằng hình thang có hai cạnh đáy không bằng nhau, hai cạnh bên bằng nhau là hình thang cân
Giải
|
GT |
Hình thang ABCD; AB // CD; AB < CD; AD = BC; AD không song song BC. |
|
KL |
ABCD là hình thang cân |
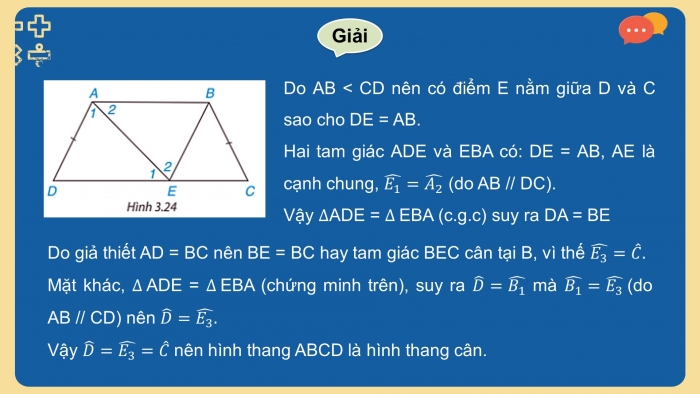
Do AB < CD nên có điểm E nằm giữa D và C sao cho DE = AB.
Hai tam giác ADE và EBA có: DE = AB, AE là cạnh chung, (do AB // DC).
Vậy ADE = EBA (c.g.c) suy ra DA = BE
Do giả thiết AD = BC nên BE = BC hay tam giác BEC cân tại B, vì thế
Mặt khác, ADE = EBA (chứng minh trên), suy ra mà (do AB // CD) nên
Vậy nên hình thang ABCD là hình thang cân.
Bài 3.9 (SGK – tr56)
Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?
Giải
Ta có tứ giác ABCD có và bù nhau.
Gọi Ax là tia đối của tia AD thì:
AB // DC (hai dóc đồng vị bằng nhau)
Vậy ABCD là hình thang với hai đáy AB và CD.
LUYỆN TẬP
BÀI TẬP TRẮC NGHIỆM
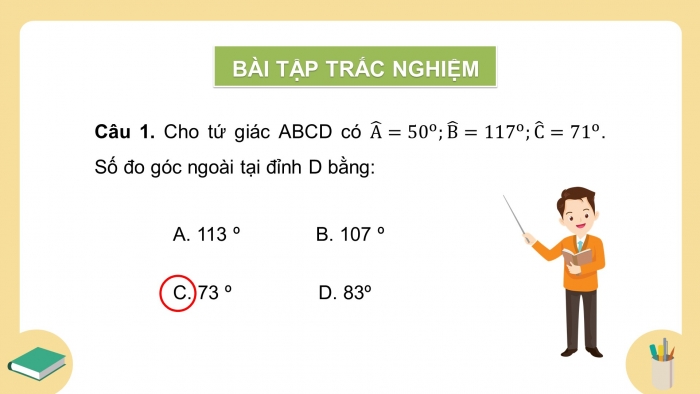
Câu 1. Cho tứ giác ABCD có . Số đo góc ngoài tại đỉnh D bằng:
- 113 º B. 107 º
- 73 º D. 83º
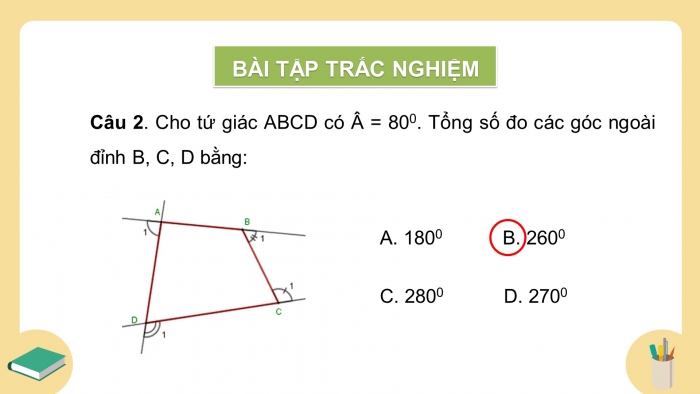
Câu 2. Cho tứ giác ABCD có Â = 800. Tổng số đo các góc ngoài đỉnh B, C, D bằng:
- 1800B. 2600
- 2800D. 2700
Câu 3. Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
- ABCD là hình thang cân
- AC = BD
- BC = AD
- Tam giác AOD cân tại O.
Câu 4. Cho hình thang cân ABCD có AB // CD và = 125o. Tính ?
- 125º B. 65º
- 90º D. 55º
Câu 5. Cho tam giác ABC cân tại A, các đường phân giác BE, CF. So sánh BF, EF.
- BF = EF B. BF < EF
- BF > EF D. Không so sánh được
Bài 3.10 (SGK – tr56)
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết , tính số đo các góc của hình thang đó.
Giải
Ta có cân tại A (AB = AD (gt)).
Vì AB // CD nên .
Mà ABCD là hình thang cân nên ; .
Bài 3.11 (SGK – tr56)
Tính số đo các góc của tứ giác ABCD trong Hình 3.26.
Giải
cân tại A nên .
Trên hình, ; nên
cân tại C nên
Tứ giác ABCD có .
VẬN DỤNG
Bài 3.12 (SGK – tr56)
Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
- a) Chứng minh tứ giác APMR là hình thang cân
- b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
- c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
Giải
- a) Tứ giác APMR là hình thang do MR // AP.
Có (do MP // CB) nên APMR là hình thang cân.
- b) Tương tự câu a, ta có các tứ giác BQMP và CRMQ là những hình thang cân;
suy ra RP = MA, PQ = MB, QR = MC (hai đường chéo của hình thang cân).
Chu vi của tam giác PQR là:
.
- c) Tam giác PQR làm tam giác đều có nghĩa là PQ = QR = RP tức là MB = BC = MA.
Vậy M cách đều ba đỉnh A, B, C tức M là trọng tâm của tam giác đều ABC.
BÀI TẬP THÊM
Hình ảnh về file sile, ppt trình chiếu





.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Bài giảng điện tử toán 8 KNTT, giáo án điện tử toán 8 kết nối bài: Luyện tập chung chương III (1 tiết), giáo án powerpoint toán 8 KNTT bài: Luyện tập chung chương III (1 tiết)
