Tải giáo án Powerpoint Toán 8 KNTT Luyện tập chung (tr.87)

CHÀO MỪNG CÁC EM ĐÃ ĐẾN VỚI BÀI HỌC HÔM NAY!

CHƯƠNG IV: ĐỊNH LÍ THALÈS

LUYỆN TẬP CHUNG

Ví dụ 1

Tìm độ dài x trong Hình 4.27

Giải

Ta có  (giả thiết), mà hai góc này ở vị trí đồng vị nên MN // BC (dấu hiệu nhận biết hai đường thẳng song song).

Suy ra  (định lí Thalès trong tam giác) hay

Suy ra

Ví dụ 2:

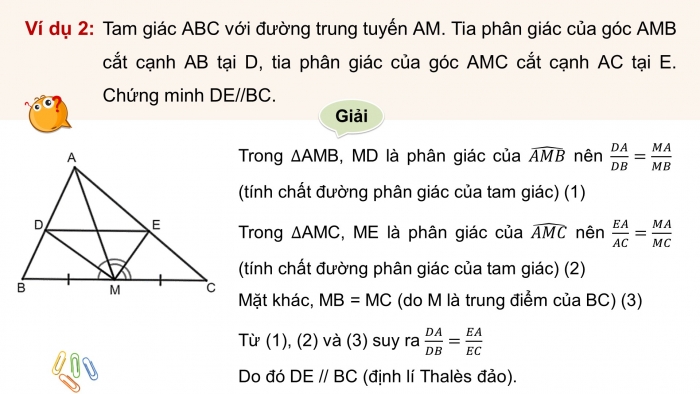
Tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB tại D, tia phân giác của góc AMC cắt cạnh AC tại E. Chứng minh DE//BC.

Giải

Trong AMB, MD là phân giác của  nên  (tính chất đường phân giác của tam giác) (1)

Trong AMC, ME là phân giác của  nên  (tính chất đường phân giác của tam giác) (2)

Mặt khác, MB = MC (do M là trung điểm của BC) (3)

Từ (1), (2) và (3) suy ra

Do đó DE // BC (định lí Thalès đảo).

Ví dụ 3:

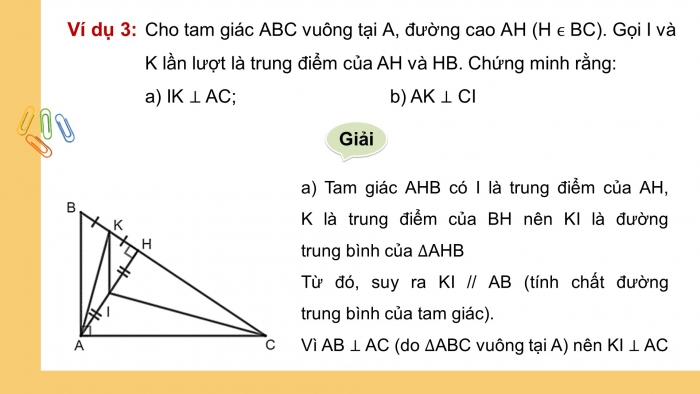
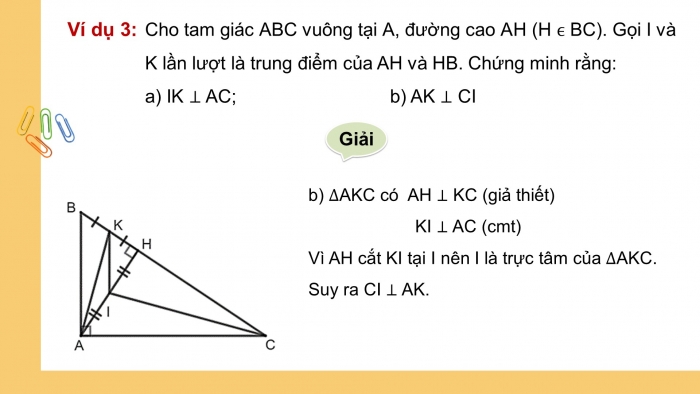
Cho tam giác ABC vuông tại A, đường cao AH (H  BC). Gọi I và K lần lượt là trung điểm của AH và HB. Chứng minh rằng:

1. a) IK AC;              b) AK  CI

Giải

1. a) Tam giác AHB có I là trung điểm của AH, K là trung điểm của BH nên KI là đường trung bình của AHB

Từ đó, suy ra KI // AB (tính chất đường       trung bình của tam giác).

Vì AB  AC (do ABC vuông tại A) nên KI  AC

1. b) AKC có AH KC (giả thiết)

                      KI  AC (cmt)

Vì AH cắt KI tại I nên I là trực tâm của AKC. Suy ra CI  AK.

LUYỆN TẬP

CÂU HỎI TRẮC NGHIỆM

Câu 1. Một tam giác đều có độ dài cạnh bằng 14cm. Độ dài một đường trung bình của tam giác đó là:

1. 34 cm B. 7 cm
2. 6,5 cm D. 21 cm

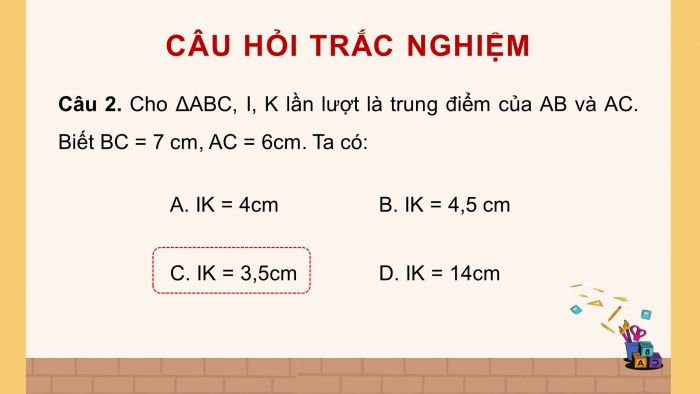
Câu 2. Cho ΔABC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 7 cm, AC = 6cm. Ta có:

1. IK = 4cm B. IK = 4,5 cm
2. IK = 3,5cm D. IK = 14cm

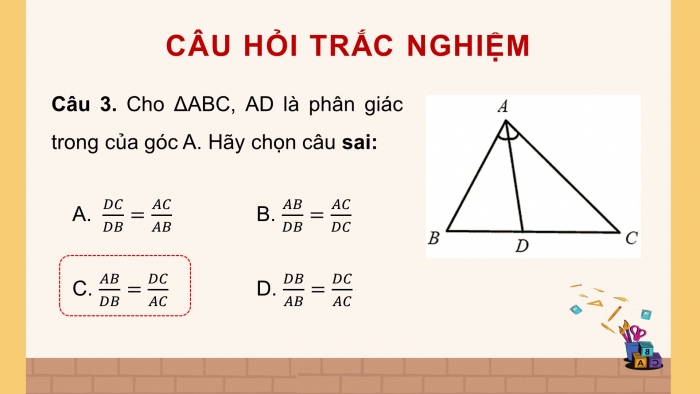
Câu 3. Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu sai:

1. B.
2. D.

Câu 4. Cho tam giác ABC có chu vi 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, CA. Chu vi của tam giác EFP là:

1. 17 cm B. 33 cm
2. 15 cm D. 16 cm

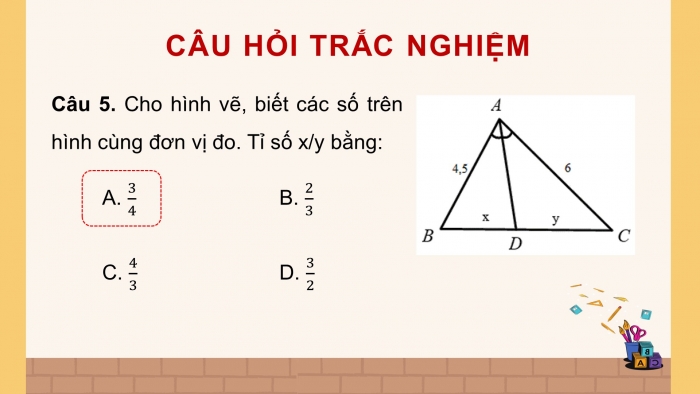
Câu 5. Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số x/y bằng:

1. B.
2. D.

Bài 4.13 (SGK – tr.88)

Tìm độ dài x trong Hình 4.30

Giải

Ta có  =  mà hai góc này ở vị trí so le trong nên MN // DE.

Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:

 hay 

Suy ra  (đvđd).

Bài 4.14 (SGK – tr.88)

Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.

1. a) Chứng minh EK // CD, FK // AB.
2. b) So sánh EF và (AB + CD).

Giải:

1. a) Vì E, K lần lượt là trung điểm của AD, AC 

nên EK là đường trung bình của tam giác ACD suy ra EK // CD.

Vì K, F lần lượt là trung điểm của AC, BC 

nên KF là đường trung bình của tam giác ABC suy ra KF // AB.

Vậy EK // CD, FK // AB.

1. b) Vì EK là đường trung bình của tam giác ACD nên EK = CD

Vì KF là đường trung bình của tam giác ABC nên KF =  AB

Do đó EK + KF =  (AB + CD)   (1)

Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: EF < EK + KF          (2)

Từ (1) và (2) ta suy ra EF <  (AB + CD).

VẬN DỤNG

                                        Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng 

Giải

Theo đề bài, AD là tia phân giác của , áp dụng tính chất đường phân giác vào tam giác ABC,       ta có:  (1)

Đường thẳng qua D song song với AB cắt AC      tại E hay DE // AB, áp dụng định lí Thalès vào       tam giác ABC, ta có :  (2)

Từ (1) và (2) suy ra  (đpcm).

                                        Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.

1. a) Tính độ dài các đoạn thẳng DB và DC.
2. b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Giải

1. a) Áp dụng tính chất đường phân giác, ta có:

, suy ra 

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

Do đó, DB =  (cm); DC =  (cm).

1. b) Hai tam giác ABD và ACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.

Ta có:

Suy ra

Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng .

Bài 4.17 (SGK – tr.88)

                                        Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM² = MN . MK 

Giải