Tải giáo án Powerpoint Toán 11 KNTT Bài 1: Giá trị lượng giác của góc lượng giác

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC HÔM NAY!

KHỞI ĐỘNG

Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400km (hình dưới). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi đó nằm trong góc  ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu Kilomet trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.

CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC

NỘI DUNG BÀI HỌC

Góc lượng giác

Đơn vị đo góc và độ dài cung tròn

Giá trị lượng giác của góc lượng giác

Quan hệ giữa các giá trị lượng giác

1 GÓC LƯỢNG GIÁC

1. a) Khái niệm góc lượng giác và số đo của góc lượng giác

HĐ 1:

Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2.

1. a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?
2. b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của kim đồng hồ để nó chỉ đúng số 12?
3. c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?

Giải

1. a) Phải quay kim phút một khoảng bằng vòng tròn.
2. b) Phải quay kim phút một khoảng bằng vòng tròn.
3. c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó là quay ngược chiều kim đồng hồ và quay theo chiều quay của kim đồng hồ.

KẾT LUẬN

Trong mặt phẳng, cho hai tia Ou, Ov. Xét tia Om cùng nằm trong mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou, tia cuối Ov và kí hiệu là (Ou, Ov).

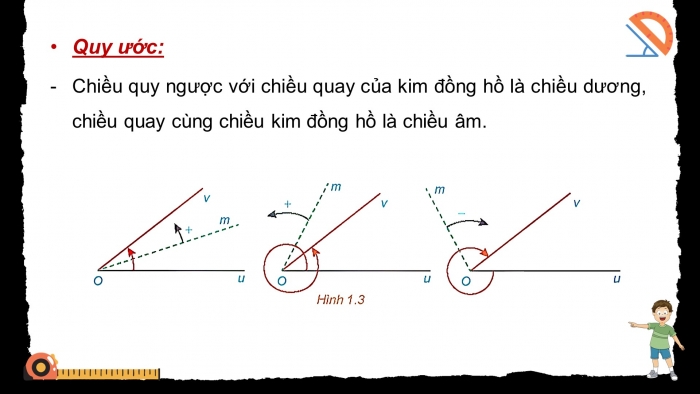
• Quy ước:
  • Chiều quy ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.
• Số đo của góc lượng giác:
  • Nếu tia Om quay theo chiều dương đúng một vòng ta nói tia Om quay góc 360º, quay đúng 2 vòng ta nói nó quay góc 720º; quay theo chiều âm nửa vòng ta nói nó quay góc -180º, quay theo chiều âm 1,5 vòng ta nói nó quay góc -1,5.360º = -540º,….
  • Khi tia Om quay góc thì ta nói góc lượng giác mà tia đó quét nên có số đo  Số đo lượng giác có tia đầu Ou, tia cuối Ov được kí hiệu là sđ(Ou, Ov).

KẾT LUẬN

Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo góc của nó.

Chú ý:

Cho hai tia Ou, Ov có vô số góc lượng giác tia đầu Ou, tia cuối Ov.                Mỗi góc lượng giác như thế đều kí hiệu là (Ou, Ov).

Số đo của các góc lượng giác này sai khác nhau một bội nguyên của 360º.

                                      Cho góc hình học  có số đo  (H.1.4). Xác định số đo của các góc lượng giác và

Giải

Ta có:

• Các góc lượng giác tia đầu , tia cuối có số đo là
• Các góc lượng giác tia đầu , tia cuối có số đo là

LUYỆN TẬP 1

Cho góc hình học  °. Xác định số đo của góc lượng giác

 trong mỗi trường hợp sau:

Giải

Góc lượng giác tia đầu Ou, tia cuối Ov, quay theo chiều dương có số đo là: °

Góc lượng giác có tia đầu Ou, tia cuối Ov, quay theo chiều âm có số đo là:

1. b) Hệ thức chasles

HĐ 2:

Cho ba tia với số đo của các góc hình học  và  lần lượt là  và 

1. a) Xác định số đo của ba góc lượng giác , và được chỉ ra ở Hình 1.5.
2. b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để

Giải

1. a) Quan sát Hình 1.5 ta có:

sđ(Ou, Ov) = 30°; sđ(Ov, Ow) = 45°;

sđ(Ou, Ow) = – (360° – 30° – 45°) = – 285°.

1. b)  Ta có:

sđ(Ou, Ov) + sđ(Ov, Ow) = 30° + 45° = 75°.

Lại có: – 285° + 1.360° = 75°.

Vậy tồn tại một số nguyên k = 1 để

sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.a

KẾT LUẬN

Hệ thức Chasles: Với ba tia Ou, Ov, Ow bất kì, ta có:

Sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360º

Nhận xét: Từ hệ thức Chasles, ta suy ra: Với ba tia tùy ý Ox, Ou, Ov ta có:

Sđ(Ou, Ov) = sđ(Ox, Ov) – sđ(Ox, Ou) + k360º .

Hệ t thực này đống vai trò quan trọng trong việc tính toán số đo của góc lượng giác.

Ví dụ 2: (SGK – tr7)

Cho một góc lượng giác có số đo  và một góc lượng giác  có số đo. Tính số đo của các góc lượng giác  

Giải

Số đo của các góc lượng giác tia đầu , tia cuối  là

Vậy các góc lượng giác  có số đo là

LUYỆN TẬP 2

Cho một góc lượng giác có số đo ° và một góc lượng giác

có số đo °. Tính số đo của các góc lượng giác 

Giải

Số đo của các góc lượng giác tia đầu Ou, tia cuối Ov là:

Vậy các góc lượng giác (Ou, Ov) có số đo là 210° + m360° (m ∈ ℤ).

2 ĐƠN VỊ ĐO GÓC VÀ ĐỘ DÀI CUNG TRÒN