Tải giáo án Powerpoint Toán 11 KNTT Bài 16: Giới hạn của hàm số
Tải bài giảng điện tử powerpoint Toán 11 kết nối tri thức Bài 16: Giới hạn của hàm số. Bài học được thiết kể đẹp mắt, nội dung giảng dạy hay nhiều trò chơi và video phong phú thu hút học sinh tập trung nắm bắt kiến thức quan trong. Giáo án tải về chỉnh sửa được. Kéo xuống để xem chi tiết
Rõ nét về file powerpoint trình chiếu. => Xem thêm
CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY!
KHỞI ĐỘNG
Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức
Trong đó là khối lượng của vật khi nó đứng yên, là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?
CHƯƠNG V. GIỚI HẠN.
HÀM SỐ LIÊN TỤC
BÀI 16: GIỚI HẠN
CỦA HÀM SỐ
NỘI DUNG BÀI HỌC
Giới hạn hữu hạn của hàm số tại một điểm
Giới hạn hữu hạn của hàm số tại vô cực
Giới hạn vô cực của hàm số tại một điểm
01 GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂMHĐ 1:
HĐ 1:
Nhận biết khái niệm giới hạn tại một điểm
Cho hàm số
- a) Tìm tập xác định của hàm số .
- b) Cho dãy số . Rút gọn và tính giới hạn của dãy với .
- c) Với dãy số bất kì sao cho và , tính và tìm .
Trả lời:
- a) Biểu thức có nghĩa khi
Do đó, tập xác định của hàm số là .
- b) Ta có:
- c) Ta có:
Vì và với mọi nên
Do đó, .
KHÁI NIỆM
Giả sử là một khoảng chứa điểm và hàm số xác định trên khoảng có thể trừ điểm . Ta nói hàm số có giới hạn là số L khi dần tới nếu với dãy số bất kì, , và , ta có , kí hiệu hay khi .
Ví dụ 1
Cho hàm số . Chứng tỏ rằng
Giải:
Lấy dãy số bất kì sao cho và . Ta có
Do đó
Vậy
QUY TẮC
- a) Nếu và thì:
- b) Nếu với mọi và thì và .
Chú ý:
+) với là hằng số. +) với .
Ví dụ 2
Cho và . Tính các giới hạn sau:
Giải:
Ta có . Mặt khác, ta thấy
- a) Ta có
Ta có . Mặt khác, ta thấy
- b) Ta có
Ví dụ 3
Tính
Giải:
Do mẫu thức có giới hạn là 0 khi nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số.
Chú ý rằng
Do đó
LUYỆN TẬP 1
Tính
Giải
Do mẫu thức có giới hạn là 0 khi nên ta không thể áp dụng trực tiếp quy tắc tính giới hạn của thương hai hàm số.
Ta có:
Do đó
HĐ 2:
Nhận biết khái niệm giới hạn một bên
Cho hàm số
- a) Cho và Tính và .
- b) Tìm giới hạn của các dãy số và .
- c) Cho các dãy số và bất kì sao cho và , tính và
Trả lời
- a) Ta có: với mọi với mọi .
Do đó,
Ta cũng có: với mọi với mọi .
Do đó,
- b) Ta có
- c) Ta có
Vì , suy ra và với mọi .
Do đó, và
Vậy và .
KHÁI NIỆM
- Cho hàm số xác định trên khoảng . Ta nói số là giới hạn bên phải của khi nếu với dãy số bất kì thỏa mãn và , ta có , kiếu hiệu .
- Cho hàm số xác định trên khoảng . Ta nói số là giới hạn bên trái của khi nếu với dãy số bất kì thỏa mãn và , ta có , kí hiệu .
Ví dụ 4
Cho hàm số
Tính và
Giải:
Với dãy số bất kì sao cho và , ta có
Do đó
Tương tự, với dãy số bất kì mà ta có , cho nên .
Chú ý
khi và chỉ khi
LUYỆN TẬP 2
Hình ảnh về file sile, ppt trình chiếu






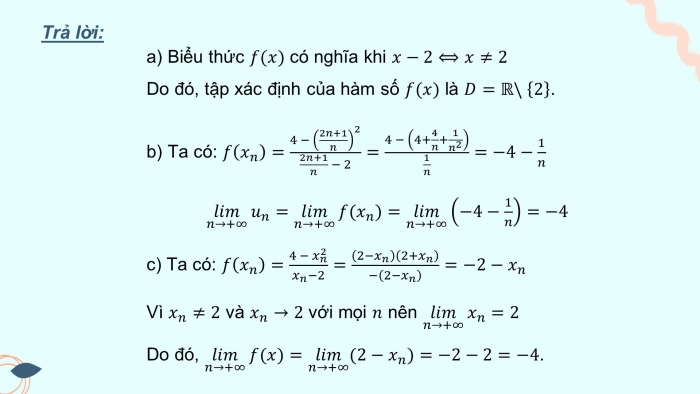



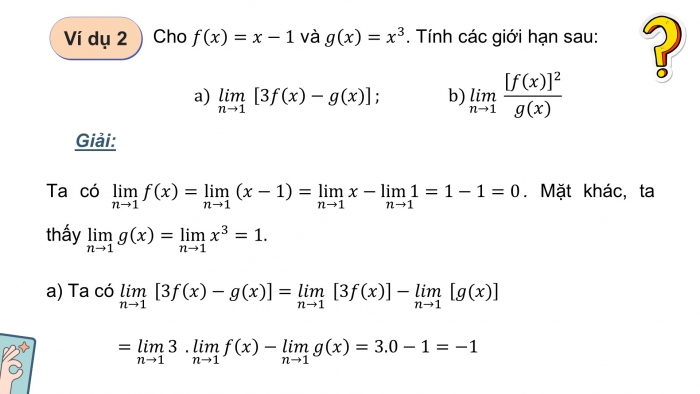
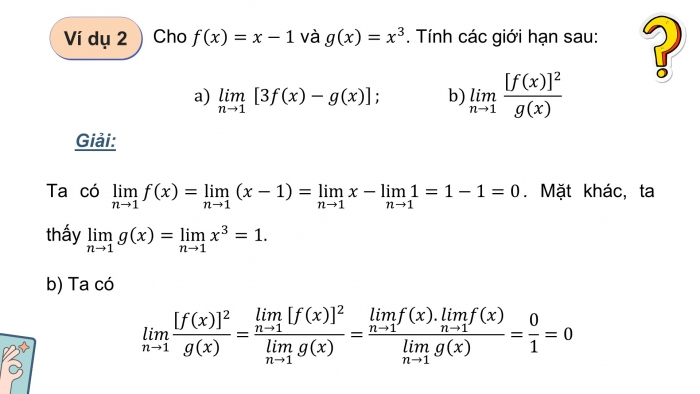
.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Bài giảng điện tử Toán 11 KNTT, Tải giáo án Powerpoint Toán 11 kết nối Bài 16: Giới hạn của hàm số, giáo án powerpoint Toán 11 kết nối tri thức Bài 16: Giới hạn của hàm số
