Tải giáo án Powerpoint Toán 11 KNTT Bài 23: Đường thẳng vuông góc với mặt phẳng

CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC!

KHỞI ĐỘNG

Hầu hết các công trình kiến trúc đều được xây dựng theo phương thẳng đứng để có thể vững chãi, mặc dù vậy, cũng có những công trình có phương nghiêng.

Nếu đứng tại Quảng trường màu nhiệm ở Pisa bằng mắt thường, ta có thể cảm nhận rằng tháp ngoài cùng bên phải trong hình là nghiêng và các công trình còn lại đều thẳng đứng.

CHƯƠNG VII: QUAN HỆ
VUÔNG GÓC TRONG KHÔNG GIAN

BÀI 23. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

NỘI DUNG BÀI HỌC

Đường thẳng vuông góc với mặt phẳng

Tính chất

Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

• HĐ1

Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).

1. a) Từ quan sát trên, hãy giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng đi qua B trên sàn nhà.
2. b) Giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng trên sàn nhà.

Giải

1. a) Trong quá trình đóng - mở cánh cửa:

• Đường thẳng cố định vì luôn đi qua hai bản lề cố định.
• Đường thẳng trên mặt sàn và luôn đi qua điểm  cố định (là giao của đường thẳng  và mặt sàn).

Vì đường thẳng  quay quanh điểm  và  nên  vuông góc với các đường thẳng trên mặt sàn và đi qua .

1. b) Lấy đường thẳng bất kì trên mặt sàn.

Xét  là đường thẳng trên mặt sàn, đi qua  và song song với .

Khi đó .

KẾT LUẬN

Đường thẳng  được gọi là vuông góc với mặt phẳng  nếu  vuông góc với mọi đường thẳng nằm trong

Chú ý: Khi  vuông góc với , ta còn nói  vuông góc với  hoặc  và  vuông góc với nhau, kí hiệu

Nếu đường thẳng  và mặt phẳng vuông góc với nhau thì chúng có cắt nhau hay không?

 và (P) cắt nhau.

Vì nếu trái lại thì  song song hoặc nằm trên  

Khi đó, tồn tại đường thẳng  

//  

Do đó, , mâu thuẫn với giả thiết  .

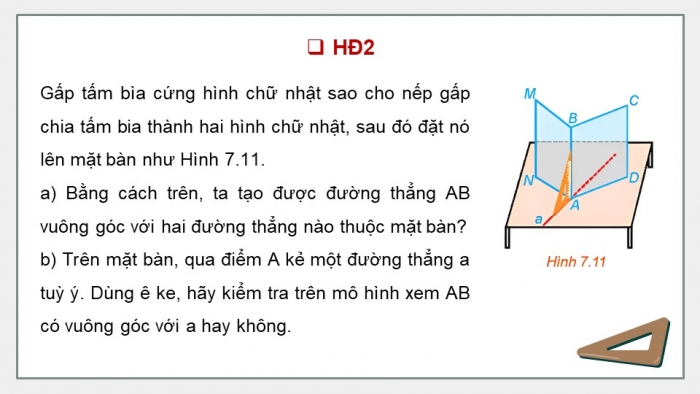
• HĐ2

Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bia thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11.

1. a) Bằng cách trên, ta tạo được đường thẳng AB vuông góc với hai đường thẳng nào thuộc mặt bàn?
2. b) Trên mặt bàn, qua điểm A kẻ một đường thẳng a tuỳ ý. Dùng ê ke, hãy kiểm tra trên mô hình xem AB có vuông góc với a hay không.

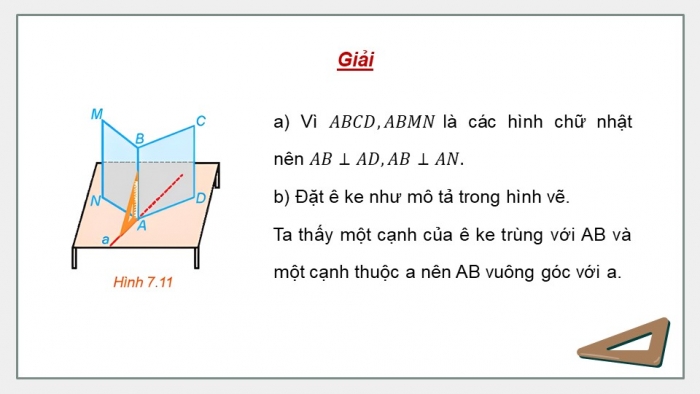
Giải

1. a) Vì là các hình chữ nhật nên
2. b) Đặt ê ke như mô tả trong hình vẽ.

Ta thấy một cạnh của ê ke trùng với AB và một cạnh thuộc a nên AB vuông góc với a.

Kết luận

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với các cạnh còn lại hay không?

Vì đường thẳng vuông góc với hai cạnh của tam giác nên vuông góc với mặt phẳng chứa tam giác.

Nên đường thẳng vuông góc với cạnh thứ ba.

Ví dụ 1:

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và cạnh SA vuông góc với các cạnh AB, AC. Chứng minh rằng BC  (SAB).

Giải

Vì SA vuông góc với hai đường thẳng AB và AC nên SA  (ABC). Suy ra SA BC.

Tam giác ABC vuông tại B nên BC BA.

Vì BC vuông góc với hai đường thẳng SA và BA nên BC  (SAB).