Tải giáo án Powerpoint Toán 11 KNTT Bài 9: Các số đặc trưng đo xu thế trung tâm

CHÀO MỪNG TẤT CẢ CÁC EM ĐẾN VỚI TIẾT HỌC!

KHỞI ĐỘNG

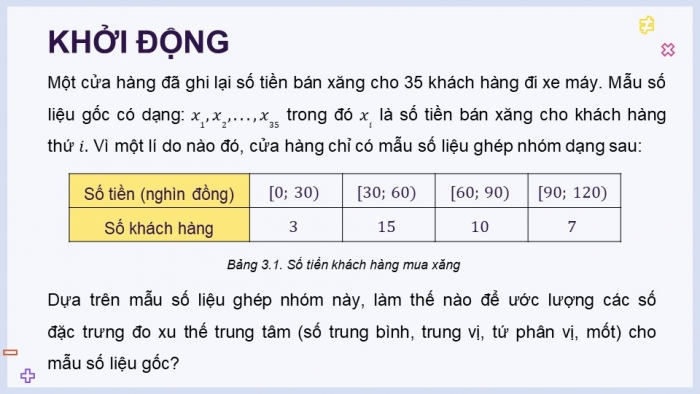
Một cửa hàng đã ghi lại số tiền bán xăng cho 35 khách hàng đi xe máy. Mẫu số liệu gốc có dạng: _­ trong đó  là số tiền bán xăng cho khách hàng thứ  Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau:

Bảng 3.1. Số tiền khách hàng mua xăng

Dựa trên mẫu số liệu ghép nhóm này, làm thế nào để ước lượng các số       đặc trưng đo xu thế trung tâm (số trung bình, trung vị, tứ phân vị, mốt) cho mẫu số liệu gốc?

CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM

BÀI 9: CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM

NỘI DUNG BÀI HỌC

Số trung bình của mẫu số liệu ghép nhóm

Trung vị của mẫu số liệu ghép nhóm

Tứ phân vị của mẫu số liệu ghép nhóm

Mốt của mẫu số liệu ghép nhóm

01 SỐ TRUNG BÌNH CỦA MẪU SỐ LIỆU GHÉP NHÓM

HĐ 1:

Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên.

1. a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được.
2. b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp không?
3. c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm này không?

Trả lời:

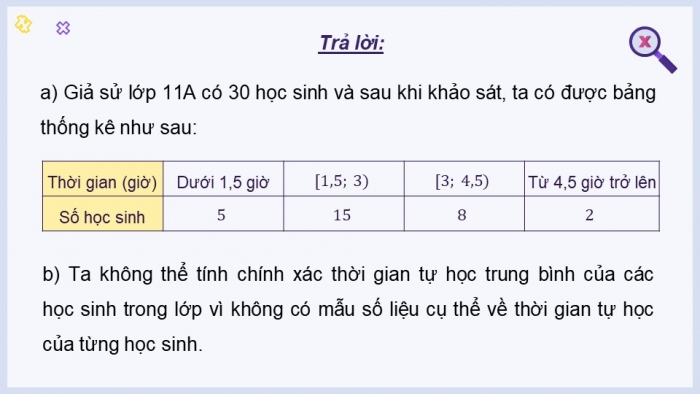
1. a) Giả sử lớp 11A có 30 học sinh và sau khi khảo sát, ta có được bảng thống kê như sau:

1. b) Ta không thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp vì không có mẫu số liệu cụ thể về thời gian tự học của từng học sinh.
2. c) Có thể tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm bằng cách chọn thời gian đại diện cho mỗi nhóm, sau đó sử dụng tần số tương ứng để tính số trung bình, cụ thể:

• Thời gian tự học dưới giờ, ta chọn giá trị đại diện là  giờ, tần số tương ứng là 5.
• Thời gian tự học từ 1,5 đến dưới 3 giờ, ta chọn giá trị đại diện là

tần số tương ứng là 15.

• Thời gian tự học từ 3 đến dưới 4,5 giờ, ta chọn giá trị đại diện là

tần số tương ứng là 8.

• Thời gian tự học là từ 4,5 giờ trở lên, ta chọn giá trị đại diện là 5,25, tần số tương ứng là 2.

 Số trung bình là:

Vậy thời gian tự học trung bình của học sinh lớp 11A xấp xỉ khoảng 2,6 giờ.

CÔNG THỨC

Số trung bình của mẫu số liệu ghép nhóm là .

Trong đó  là cỡ mẫu và

 (với i = 1,…,k) là giá trị đại diện của nhóm .

Chú ý:

Đối với số liệu rời rạc, người ta thường cho các nhóm dưới dạng , trong đó . Nhóm  được hiểu là nhóm gồm các giá trị .      Khi đó, ta cần hiệu chỉnh mẫu dữ liệu ghép nhóm để đưa về dạng bảng 3.2      trước khi thực hiện tính toán các số đặc trưng bằng hiệu chỉnh nhóm  với  thành nhóm . Chẳng hạn, với dữ liệu ghép nhóm điểm thi môn Toán trong bảng 3.3 sau khi hiệu chỉnh ta được bảng 3.4.

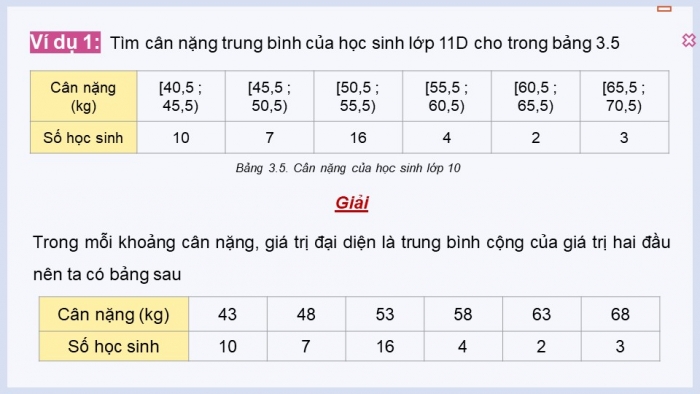
Ví dụ 1:

Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng 3.5

Bảng 3.5. Cân nặng của học sinh lớp 10

Giải

Trong mỗi khoảng cân nặng, giá trị đại diện là trung bình cộng của giá trị hai đầu nên ta có bảng sau

Tổng số học sinh là n = 42. Cân nặng trung bình của học sinh lớp 11D là:

LUYỆN TẬP 1

Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.

Trả lời:

Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:

Tổng số học sinh là .

Thời gian xem ti vi trung bình trong tuần trước của các học sinh là

(giờ)

Ý NGHĨA

Số trung bình của mẫu số liệu ghép nhóm xấp xỉ cho số trung bình của mẫu số liệu gốc, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.

02 TRUNG VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM

HĐ 2:

Cho mẫu số liệu ghép nhóm về chiều cao của 21 câu na giống.

Gọi x₁, x₂, ..., x₂₁ là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, x₁, ..., x₃ thuộc [0; 5), x₄, ..., x₁₁ thuộc [5; 10), ... Hỏi trung vị thuộc nhóm nào?

Trả lời:

Ta có: cỡ mẫu , là số lẻ nên trung vị là giá trị chính giữa của mẫu số liệu và là giá trị ở vị trí thứ 11 của mẫu số liệu.

Mà  thuộc  nên trung vị của mẫu số liệu thuộc nhóm

• Các bước tìm số trung vị của mẫu số liệu ghép nhóm

Bước 1: Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: [).

Bước 2: Trung vị là:

Trong đó n là cỡ mẫu,  là tần số nhóm p.

Với , ta quy ước .

Ví dụ 2:

                 Thời gian (phút) truy cập Internet mỗi buổi của một số học sinh được cho trong bảng sau:

Tính trung vị của mẫu số liệu ghép nhóm này.

Giải

Cỡ mẫu là

Gọi   là thời gian truy cập Internet của 56 học sinh và giải sử dãy này   đã được sắp xếp theo thứ tự tăng dần.

Khi đó, trung vị là

Do hai giá trị  thuộc nhóm [15,5; 18,5) nên nhóm này chứa trung vị.

Do đó   và ta có:

LUYỆN TẬP 2