Tải giáo án Powerpoint Toán 11 KNTT Bài 17: Hàm số liên tục

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

CHƯƠNG V. GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 17: HÀM SỐ LIÊN TỤC

NỘI DUNG BÀI HỌC

Hàm số liên tục tại một điểm

Hàm số liên tục trên một khoảng

Một số tính chất cơ bản

01 HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

HĐ 1: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số 

Tính giới hạn  và so sánh giá trị này với .

Trả lời:

Ta có

Vậy .

KHÁI NIỆM

Cho hàm số  xác định trên khoảng  chứa điểm . Hàm số  được gọi là liên tục tại điểm  nếu .

Hàm số  không liên tục tị  được gọi là gián đoạn tại điểm đó.

Ví dụ 1

Xét tính liên tục của hàm số                        tại điểm

Giải:

Rõ ràng hàm số  xác định trên , do đó  thuộc tập xác định của hàm số.

Ta có

Vậy hàm số  liên tục tại .

Ví dụ 2

Xét tính liên tục của hàm dấu

Giải:

Ta thấy   Do đó không tồn tại giới hạn

Vậy hàm số này gián đoạn tại 0.

Chú ý

Hàm số  liên tục tại  khi và chỉ khi:

LUYỆN TẬP 1

Xét tính liên tục của hàm số

tại điểm

Giải:

Ta có:  

Do đó hàm số  liên tục tại .

02 HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

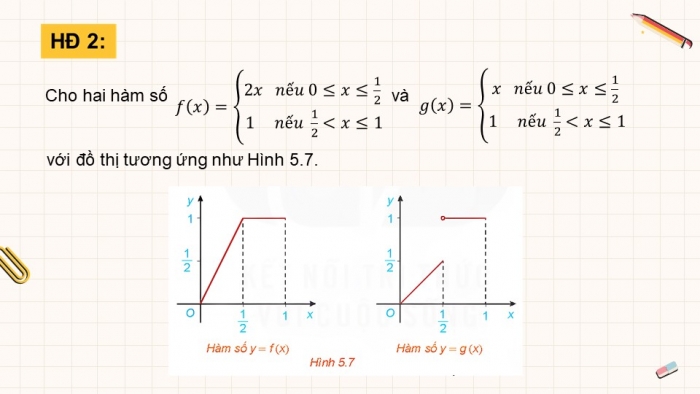
HĐ 2:

Cho hai hàm số                                              và  

với đồ thị tương ứng như Hình 5.7.

Trả lời:

Hàm số

Hàm số  xác định trên , do đó  thuộc tập xác định của hàm số.

Ta có:

Suy ra , do đó

Mà  nên

Vậy hàm số  liên tục tại

Hàm số

Hàm số  xác định trên , do đó  thuộc tập xác định của hàm số.

Ta có:

Vậy không tồn tại giới hạn của hàm số  tại , do đó hàm số     gián đoạn tại

Quan sát hình 5.7 ta thấy, đồ thị của hàm số  là đường liền trên , còn đồ thị của hàm số  trên  là các đoạn rời nhau.

KHÁI NIỆM

• Hàm số được gọi là liên tục trên khoảng  nếu nó liên tục tại mọi điểm thuộc khoảng này.
• Hàm số được gọi là liên tục trên đoạn  nếu nó liên tục trên khoảng  và

    .

Các khái niệm hàm số liên tục trên nửa khoảng như  được định nghĩa theo cách tương tự.

Ví dụ 3

Xét tính liên tục của hàm số  trên nửa khoảng .

Giải:

Ta có  với . Với  bất kì, ta có

Vậy hàm số  liên tục trên khoảng

Hơn nữa  nên  liên tục trên nửa khoảng .

Tính liên tục của một số hàm sơ cấp đã biết

• Hàm số đa thức và các hàm số ; liên tục trên .
• Các hàm số và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

Ví dụ 4

Cho hàm số                      .Tìm các khoảng trên đó hàm số  liên tục.

Giải:

Tập xác định của hàm số  là .

Vậy hàm số liên tục tên các khoảng  và .

LUYỆN TẬP 2

Tìm các khoảng trên đó hàm số                        liên tục.

Giải:

Ta thấy hàm số  là một hàm phân thức hữu tỉ. Vậy hàm số này liên tục trên các khoảng tập xác định của chúng:  và .

03 MỘT SỐ TÍNH CHẤT CƠ BẢN