Tải giáo án Powerpoint Toán 11 KNTT Bài 25: Hai mặt phẳng vuông góc

CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC
MÔN TOÁN!

KHỞI ĐỘNG

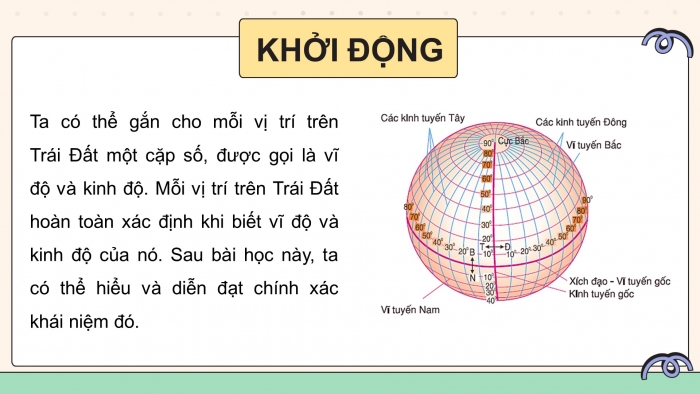
Ta có thể gắn cho mỗi vị trí trên      Trái Đất một cặp số, được gọi là vĩ độ và kinh độ. Mỗi vị trí trên Trái Đất hoàn toàn xác định khi biết vĩ độ và kinh độ của nó. Sau bài học này, ta có thể hiểu và diễn đạt chính xác khái niệm đó.

CHƯƠNG VII: QUAN HỆ

VUÔNG GÓC TRONG KHÔNG GIAN

BÀI 25: HAI MẶT PHẲNG VUÔNG GÓC

NỘI DUNG BÀI HỌC

1

Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc

2

Điều kiện để hai mặt phẳng vuông góc

Tính chất của hai mặt phẳng vuông góc

Góc nhị diện

Một số hình lăng trụ đặc biệt

Hình chóp đều và hình chóp cụt đều

1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc

HĐ 1

Cho hai mặt phẳng  và . Lấy hai đường thẳng  cùng vuông góc với , hai đường thẳng cùng vuông góc với . Tìm mối quan hệ giữa các góc và

Giải:

Vì và  cùng vuông góc với    nên chúng song song hoặc    trùng nhau.

Tương tự, và song song hoặc trùng nhau.

Vậy

Kết luận

• Cho hai mặt phẳng và Lấy các đường thẳng tương ứng vuông góc với . Khi đó góc giữa và  không phụ thuộc vào vị trí của  và được gọi là góc giữa hai mặt phẳng  và (Q).
• Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng .

Chú ý: Nếu  là góc giữa hai mặt phẳng (P) và (Q) thì .

 Góc giữa hai mặt phẳng bằng 0° khi nào, khác 0° khi nào?

Trả lời:

Xét hai đường thẳng  tương ứng vuông góc với hai mặt phẳng .

Khi đó góc giữa khi và chỉ khi , hay a và b song song hoặc trùng nhau.

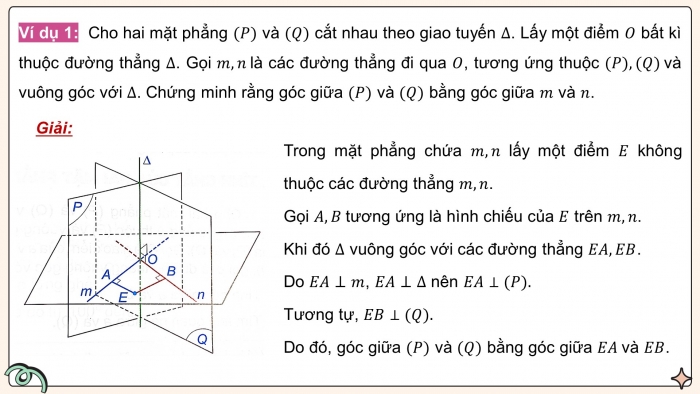
Ví dụ 1:  Cho hai mặt phẳng  và  cắt nhau theo giao tuyến . Lấy một điểm  bất kì thuộc đường thẳng . Gọi là các đường thẳng đi qua , tương ứng thuộc và vuông góc với . Chứng minh rằng góc giữa  và  bằng góc giữa  và .

Giải:

Trong mặt phẳng chứa  lấy một điểm  không thuộc các đường thẳng .

Gọi tương ứng là hình chiếu của  trên .

Khi đó  vuông góc với các đường thẳng .

Do ,  nên

Tương tự,

Do đó, góc giữa  và  bằng góc giữa và .

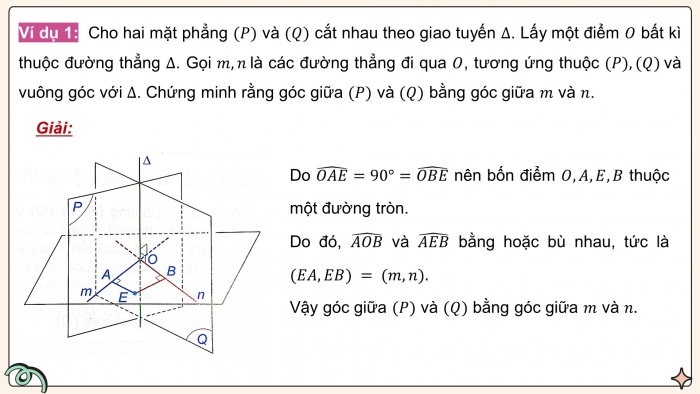
Ví dụ 1:  Cho hai mặt phẳng  và  cắt nhau theo giao tuyến . Lấy một điểm  bất kì thuộc đường thẳng . Gọi là các đường thẳng đi qua , tương ứng thuộc và vuông góc với . Chứng minh rằng góc giữa  và  bằng góc giữa  và .

Giải:

Do  nên bốn điểm  thuộc một đường tròn.

Do đó,  và  bằng hoặc bù nhau, tức là

Vậy góc giữa  và  bằng góc giữa  và

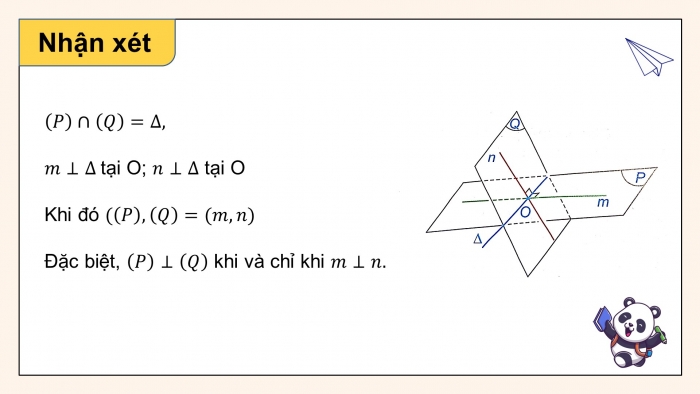
Nhận xét

tại O;  tại O

Khi đó

Đặc biệt,  khi và chỉ khi

                              Cho hình chóp , đáy  là một hình chữ nhật có tâm Chứng minh rằng hai mặt phẳng và vuông góc với nhau khi và chỉ khi  là một hình vuông.

Giải:

Gọi  là giao điểm của  và .

Vì  và

 ((  

Do đó

 là hình vuông.

2. Điều kiện để

hai mặt phẳng vuông góc

HĐ 2

Cho mặt phẳng  chứa đường thẳng  vuông góc với mặt phẳng  Lấy một đường thẳng  vuông góc với (H.7.47).

1. a) Tính góc giữa và .
2. b) Tính góc giữa và

Giải:

1. a) Vì và nên .

Vậy .

1. b) Do và tương ứng vuông góc với  và .

Do đó,   .

Kết luận

Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Ví dụ 2: Cho tứ diện  có  vuông góc với  và . Chứng minh rằng các mặt phẳng và cùng vuông góc với mặt phẳng

Giải:

Do  vuông góc với  và  nên

Mặt khác, các mặt phẳng chứa .

Do đó chúng cùng vuông góc với mặt phẳng