Tải giáo án Powerpoint Toán 8 CTST Chương 1 Bài 4: Phân tích đa thức thành nhân tử

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI GIẢNG HÔM NAY

KHỞI ĐỘNG

BÀI 4: PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ

NỘI DUNG BÀI HỌC

Phương pháp đặt nhân tử chung

Phương pháp sử dụng hằng đẳng thức

Phương pháp nhóm hạng tử

1. PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG

HĐKP1:

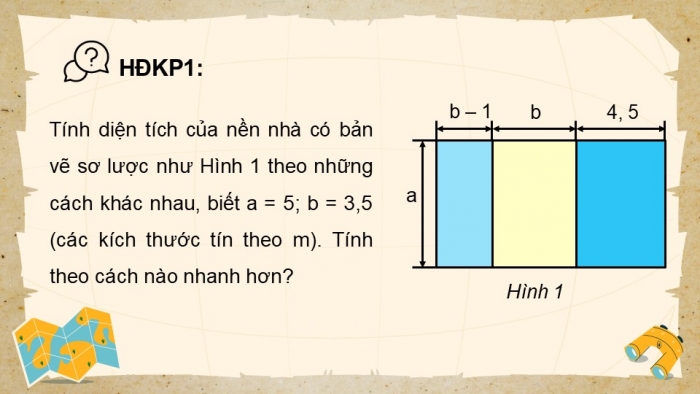
Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tín theo m). Tính theo cách nào nhanh hơn?

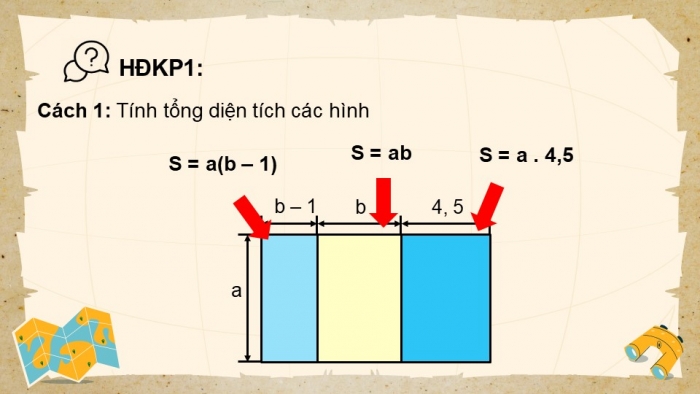
Cách 1: Tính tổng diện tích các hình

S = a(b – 1)

S = ab

S = a . 4,5

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b – 1 (m) là: a(b – 1) (m²).

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b (m) là: ab (m²).

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng 4,5 (m) là: 4,5a (m²).

Diện tích của nền nhà là: S = a(b – 1) + ab + 4,5a (m²).

Với a = 5 và b = 3,5 ta có:

S = 5.(3,5 – 1) + 5.3,5 + 4,5.5 = 5 . (3,5 – 1 + 3,5 + 4,5)

    = 5 . 10,5 = 52,5 (m²).

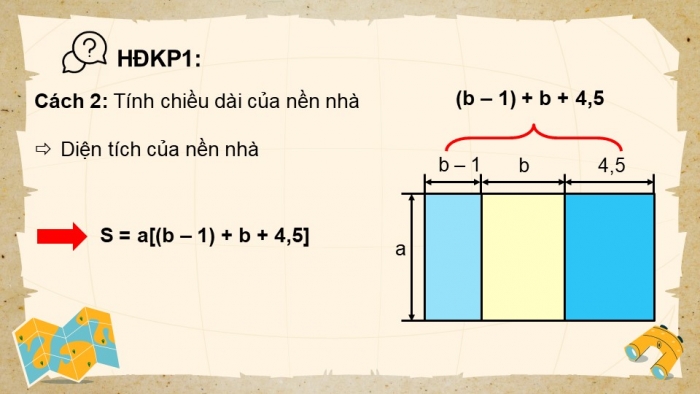
Cách 2: Tính chiều dài của nền nhà

• Diện tích của nền nhà

S = a[(b – 1) + b + 4,5]

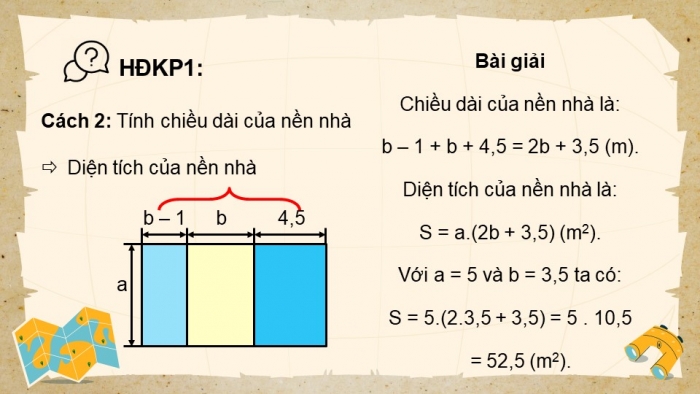
Bài giải

Chiều dài của nền nhà là:

b – 1 + b + 4,5 = 2b + 3,5 (m).

Diện tích của nền nhà là:

S = a.(2b + 3,5) (m²).

Với a = 5 và b = 3,5 ta có:

S = 5.(2.3,5 + 3,5) = 5 . 10,5

    = 52,5 (m²).

KẾT LUẬN

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đã cho thành một tích của những đa thức. Mỗi đa thức này gọi là một nhân tử của đa thức đã cho.

Ví dụ 1: SGK – tr.23

Phân tích đa thức A = 3xy – 6x²y + 12x thành nhân tử

A = 3xy – 6x²y + 12x

3xy = 3x . y

6x²y = 3x . 2xy

12x = 3x . 4

3x là nhân tử chung của các hạng tử của A

Giải

A = 3xy – 6x²y + 12x = 3x . y + 3x . 2xy + 3x . 4

   = 3x . (y – 2xy + 4)

Phương pháp đặt nhân tử chung

Thực hành 1

Phân tích các đa thức sau thành nhân tử

1. a) P = 6x – 2x³ b) Q = 5x³ – 15x²y c) R = 3x³y³ – 6xy³z + xy

Giải

1. a) P = 6x – 2x³

       = 2x . 3 – 2x . x²

       = 2x(3 – x²).

       = 2x( + x)( – x)

1. b) Q = 5x³– 15x²y

       = 5x² . x – 5x² . 3y

       = 5x²(x – 3y).

1. c) R = 3x³y³– 6xy³z + xy

       = xy . 3x²y² – xy . 6y²z + xy . 1

       = xy(3x²y² – 6y²z + 1).

2. PHƯƠNG PHÁP SỬ DỤNG HẰNG ĐẲNG THỨC

HĐKP2:

Tìm biểu thức thích hợp thay vào mỗi chỗ      , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử

1. a) 4x² – 9 = ( )² – ( )² = ….
2. b) x²y² - y² = ( )² – ( )² = ….
3. a) 4x² – 9 = (2x)² – (3)² = (2x + 3)(2x – 3)

a² – b²

= (a + b)(a – b)

Phương pháp sử dụng hằng đẳng thức

Ví dụ 2: SGK – tr.24

Phân tích các đa thức sau thành nhân tử

1. a) A = x² + 10x + 25; b) B = x³ + 8y³; c) C = 2ax² – 18ay²
2. a) A = x² + 10x + 25 = x² + 2 . x . 5 + 5² = (x + 5)²
3. b) B = x³ + 8y³ = x³ + (2y)³ = (x + 2y)[x² – x . 2y + (2y)²]

         = (x + 2y)(x² – 2xy + 4y²)

1. c) C = 2ax² – 18ay² = 2a(x² – 9y²) = 2a[x² – (3y)²]

        = 2a(x + 3y)(x – 3y)

Thực hành 2