Hướng dẫn giải nhanh Toán 8 CTST bài 1: Định lí Pythagore

1. ĐỊNH LÍ PYTHAGORE

Hoạt động 1 trang 58 sgk Toán 8 tập 1 CTST

Cho một tam giác vuông...

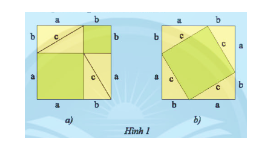
Đáp án:

Diện tích phần bìa không bị che lấp ở hình a là: $a^2 + b^2$(đơn vị diện tích).

Diện tích phần bìa không bị che lấp ở hình b là: $c^2$ (đơn vị diện tích).

$\Rightarrow a^2 + b^2 = c^2$

Thực hành 1 trang 59 sgk Toán 8 tập 1 CTST 

Tính độ dài cạnh EF, MN của các tam vuông trong Hình 3...

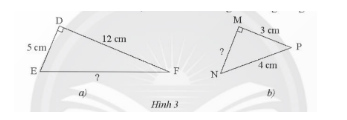
Đáp án:

a) $EF^2 = 12^2 + 5^2 = 169 => EF = 13 cm$

b) $MN^2 = 4^2 – 3^2 = 7 => MN = \sqrt{7} (cm)$

Vận dụng 1 trang 59 sgk Toán 8 tập 1 CTST

Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là...

Đáp án:

Độ dài đường chéo của ti vi là : 

$\sqrt{72^2 + 120^2} \approx 139,94 (cm) \approx 55(inch)$

2. ĐỊNH LÍ PYTHAGORE ĐẢO

Hoạt động 1 trang 59 sgk Toán 8 tập 1 CTST

Vẽ vào vở tam giác ABC...

Đáp án:

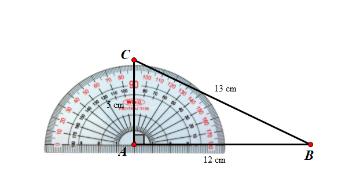
$\widehat{BAC} = 90^{\circ}$

Thực hành 2 trang 60 sgk Toán 8 tập 1 CTST

Tìm tam giác vuông trong các tam giác sau...

Đáp án:

a) $EF^2 + FK^2 = 9^2 + 12^2 = 225 ; EK^2 = 15^2 = 225 \Rightarrow \Delta EFK$ vuông tại F

b) $PR^2 + QR^2 = 10^2 + 12^2 = 244 ; PQ^2 = 17^2 = 289 \Rightarrow \Delta PQR$ không vuông

c) $DE^2 + DF^2 = 8^2 + 6^2 = 100 ; EF^2 = 10^2 = 100 \Rightarrow \Delta DEF$ vuông tại D

Vận dụng 2 trang 60 sgk Toán 8 tập 1 CTST

a) Nam dự định làm một cái eke từ ba thanh nẹp gỗ...

Đáp án:

a) Độ dài thanh nẹp còn lại là : $\sqrt{6^2+8^2} = 10 (cm)$

b) Xét $\Delta ADC : AD^2 + DC^2 = 48^2 + 36^2 = 3600$;

$AC^2 = 60^2 = 3600$

$\Rightarrow \Delta ADC$ vuông tại D $\Rightarrow \widehat{ADC}$ là góc vuông.

Xét $\Delta ABC : AB^2 + BC^2 = 36^2 + 48^2 = 3600$

$AC^2 = 60^2 = 3600$

$\Rightarrow \Delta ABC$ vuông tại B $\Rightarrow \widehat{ABC}$ là góc vuông.

3. VẬN DỤNG ĐỊNH LÍ PYTHAGORE

Thực hành 3 trang 61 sgk Toán 8 tập 1 CTST 

Tính các độ dài PN và BC...

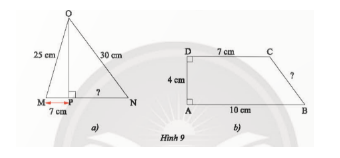
Đáp án:

a) $OP^2 = OM^2 – MP^2= 25^2 – 7^2 = 576$.

$PN^2 = ON^2 – OP^2= 30^2 – 576 = 324 \Rightarrow PN = 18 cm$

b) 

$CH = 4 cm ; HB = 10 – 7 = 3 cm$

$BC^2=CH^2 + HB^2 = 4^2 + 3^2 = 25 \Rightarrow BC = 5 cm$

Vận dụng 3 trang 61 sgk Toán 8 tập 1 CTST

Tính chiều dài cần cẩu AB trong Hình 10...

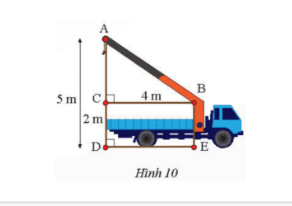
Đáp án:

$AC = 5 – 2 = 3 (m)$.

$AB^2 =AC^2 + CB^2 =3^2 + 4^2 =25  \Rightarrow AB = 5 m$

BÀI TẬP CUỐI SGK

Bài tập 1 trang 61 sgk Toán 8 tập 1 CTST

Cho tam giác ABC vuông tại A...

Đáp án:

a) $BC^2 = AB^2 + AC^2 = 7^2 + 24^2 = 625 \Rightarrow BC=25 cm$.

b) $AB^2= BC^2– AC^2 = \sqrt{13}^2-2^2=9 \Rightarrow AB=3 cm$.

c) $AC^2= BC^2– AB^2 = 25^2 – 15^2 = 400 \Rightarrow AC=20 cm$

Bài tập 2 trang 62 sgk Toán 8 tập 1 CTST

Tính độ cao của con diều so với mặt đất (Hình 11)...

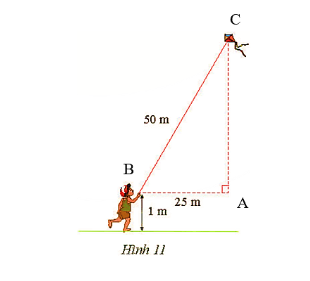
Đáp án:

$AC^2 = BC^2 - AB^2 = 50^2 -25^2 = 1 875$

$\Rightarrow AC = 25\sqrt{3} (m)$

Độ cao của con diều so với mặt đất là: 

$25\sqrt{3} + 1 \approx 44,3 (m)$ 

Bài tập 3 trang 62 sgk Toán 8 tập 1 CTST

Lần lượt tính độ dài các cạnh huyền a, b, c, d...

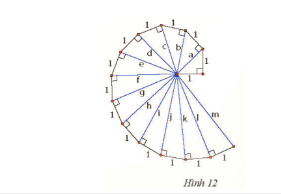
Đáp án:

$a = \sqrt{1^2 + 1^2} = \sqrt{2}$

$b = \sqrt {2 +1^2} = \sqrt{3}$

$c = \sqrt{3 + 1^2} =\sqrt{4} = 2$

$d = \sqrt{4 + 1^2} = \sqrt{5}$

Dự đoán độ dài các cạnh huyền còn lại:

$e=\sqrt{6}; f=\sqrt{7}; g=\sqrt{8}; h=\sqrt{9}; i= \sqrt{10}$;

$j= \sqrt{11}; k= \sqrt{12}= 2\sqrt{3}; l= \sqrt{13}; m=\sqrt{14}$.

Bài tập 4 trang 62 sgk Toán 8 tập 1 CTST

Chứng minh rằng tam giác ABC vuông trong các trường hợp sau...

Đáp án:

a) $AB^2 +AC^2 = 8^2 +15^2 =289$

$BC^2 = 17^2 =289$

$\Rightarrow \Delta ABC$ vuông tại A.

b) $BC^2 + AC^2 = 20^2 + 21^2 = 841$

$AB^2 = 29^2 = 841$

$\Rightarrow \Delta ABC$ vuông tại C.

c) $AB^2+BC^2 = 12^2 + 35^2 =1 369$

$AC^2 = 37^2 = 1367$

$\Rightarrow \Delta ABC$ vuông tại B

Bài tập 5 trang 62 sgk Toán 8 tập 1 CTST

Cho biết thang của một xe cứu hỏa có chiều dài 13 cm, chân thang...

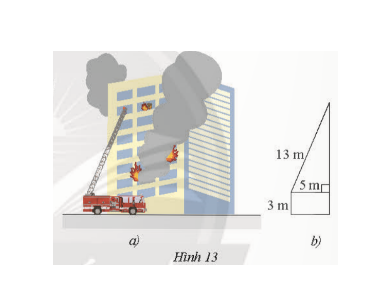
Đáp án:

Chiều cao mà thang có thể vươn tới là: 

$\sqrt{13^2 - 5^2} + 3 =15(m)$

Bài tập 6 trang 62 sgk Toán 8 tập 1 CTST

Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m...

Đáp án:

Khoảng cách từ thuyền đến ngọn hải đăng là: 

$\sqrt{25^2 + 180^2} \approx 181,73 (m)$