Hướng dẫn giải nhanh Toán 8 CTST bài 3: Hình thang - Hình thang cân

1. HÌNH THANG - HÌNH THANG CÂN

Hoạt động 1 trang 68 sgk Toán 8 tập 1 CTST

Tứ giác ABCD…

Hướng dẫn trả lời:

AB // CD

Thực hành 1 trang 69 sgk Toán 8 tập 1 CTST

Tìm các góc chưa biết của hình thang MNPQ có hai đáy...

Hướng dẫn trả lời:

a)

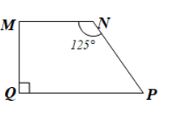
$\widehat{M} = \widehat{Q} = 90°$

$\widehat{P}= 360°-90°+90°+125°=55°$

b)

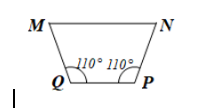
$\widehat{M} =  \widehat{N} =180°-110°=70°$

Vận dụng 1 trang 69 sgk Toán 8 tập 1 CTST 

Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân...

Hướng dẫn trả lời:

$\widehat{A}=\widehat{B}=180°-75°=105°$

Vận dụng 2 trang 69 sgk Toán 8 tập 1 CTST

Tứ giác EFGH có các góc cho như...

Hướng dẫn trả lời:

a) $\widehat{E} +  \widehat{F} = 180° \Rightarrow EH // FG \Rightarrow EHGF$ là hình thang

b) $\widehat{H} =360° -(85°+27°+95°)=153°$

2. TÍNH CHẤT CỦA HÌNH THANG CÂN

Hoạt động 3 trang 69 sgk Toán 8 tập 1 CTST

a) Cho hình thang cân...

Hướng dẫn trả lời:

a) $AD // CE =>  \widehat{A} =  \widehat{CEB}$

ABCD là hình thang cân $=>  \widehat{A} =  \widehat{B}$

$=>  \widehat{CEB} =  \widehat{B} \Rightarrow \Delta CEB$

$\widehat{CEB} = \widehat{B} \Rightarrow \Delta CEB$ cân tại C.

Xét ΔAED và ΔCDE có:

$\widehat{AED} = \widehat{CDE}$

Chung cạnh ED

$\widehat{ADE} = \widehat{CED}$

=> ΔAED=ΔCDE (g.c.g) => AD = CE

ΔCEB cân tại C (cmt)   => BC = CE

$\Rightarrow AD =BC $

b) QPNM là hình thang cân => QM =PN

QPNM là hình thang cân =>$ \widehat{NMQ} = \widehat{MNP}$

Xét ΔMQN và ΔNPM có:

Chung cạnh MN

$\widehat{NMQ} = \widehat{MNP}$

QM =PN

=> ΔMQN=ΔNPM (c.g.c) => QN = MP

Thực hành 2 trang 70 sgk Toán 8 tập 1 CTST

Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy...

Hướng dẫn trả lời:

MP = QN ; MQ = PN

Vận dụng 3 trang 69 sgk Toán 8 tập 1 CTST

Một khung cửa sổ hình thang cân có chiều cao...

Hướng dẫn trả lời:

Kẻ BK ⊥ DC.

AB // DC => BK ⊥ AB => $\widehat{ABK} = 90^{\circ}$

Tứ giác AHKB có: 

$\widehat{ABK}=\widehat{AHK}=\widehat{HKB} = 90^{\circ}$ => AHKB là hình chữ nhật

=> HK = AB = 1m

∆AHD= ∆BKC (cạnh huyền – góc nhọn)

=> HD = KC = (DC – HK) : 2 = ( 3-1) : 2 = 1m => HC = 2m

∆AHD vuông tại H=>$AD^2 = AH^2 + DH^2 = 3^2 + 1^2 =10$

$\Rightarrow AD = \sqrt{10} (m) = BC$

∆AHC vuông tại H => $AC^2 = AH^2 + HC^2 = 3^2 + 2^2 =13$

$\Rightarrow AC = \sqrt{13} (m) = BD$

3. DẤU HIỆU NHẬN BIẾT HÌNH THANG CÂN

Hoạt động 3 trang 70 sgk Toán 8 tập 1 CTST

Cho hình thang ABCD...

Hướng dẫn trả lời:

a) DB // CE => $\widehat{DBC}=\widehat{ECB}$

AE // DC => $\widehat{DCB}=\widehat{EBC}$

ΔDBC=ΔECB (g.c.g) => BD = EC

BD = AC (gt)

$\Rightarrow$ REC= AC => ΔACE cân tại C

b) BD // EC => $\widehat{ABD}=\widehat{CEB}$

ΔACE cân tại C => $\widehat{CAE}=\widehat{CEA}$

$\Rightarrow \widehat{ABD}=\widehat{CAE}$

$\Rightarrow$ ΔABD=ΔBAC (c.g.c).

Thực hành 3 trang 71 sgk Toán 8 tập 1 CTST

Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở...

Hướng dẫn trả lời:

Hình thang cân : ABCD ; FGHE

Vận dụng 4 trang 71 sgk Toán 8 tập 1 CTST 

Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân...

Hướng dẫn trả lời:

ΔMHK=ΔKNM (cạnh huyền – góc nhọn) => HK = NM = 6 cm

ΔMHQ=ΔNKP (cạnh huyền – góc nhọn) => HQ = KP

$\Rightarrow$ HQ = KP= QP - HK : 2 = 10 - 6 : 2 = 2cm

$\Rightarrow$ HP=6+2=8cm

MHP vuông tại H ta có: 

$MH^2 = MP^2 + HP^2 = (8\sqrt{2})^2  -8^2 =64$

$\Rightarrow$ MH = 8 cm.

ΔMQH vuông tại H ta có: 

$MQ^2 = MH^2 + HQ^2 = 8^2 + 2^2 =68$

$\Rightarrow MQ = 2\sqrt{17} (cm)$

BÀI TẬP CUỐI SGK

Bài tập 1 trang 71 sgk Toán 8 tập 1 CTST 

Tìm x và y ở các hình sau...

Hướng dẫn trả lời:

a) x=180°-140°=40°

b) x =180° $\widehat{Q}$=180°-60°=120°

$y = 70^{\circ}$

c) x+4x=180° ⬄5x = 180° ⬄ x=36°

d) 2x+x =180° ⬄3x=180° ⬄x = 60°.

Bài tập 2 trang 71 sgk Toán 8 tập 1 CTST

Cho tứ giác ABCD có AB = CD, BD là tia phân giác góc B. Chứng minh...

Hướng dẫn trả lời:

BD là tia phân giác của góc B =>  $\widehat{ABD}=\widehat{CBD}$

AB = AD (gt) => ΔABD cân tại A => $\widehat{ABD}=\widehat{ADB}$

$\Rightarrow \widehat{CBD}=\widehat{ADB}$

AD // BC.

ABCD là hình thang.

Bài tập 3 trang 72 sgk Toán 8 tập 1 CTST 

Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác...

Hướng dẫn trả lời:

a) BC// NM ( cùng AH) => BCMN là hình thang

b) BM là tia phân giác của $\widehat{ABC}$ 

$\Rightarrow \widehat{NBM}=\widehat{MBC}$

MN // BC => $\widehat{NMB}=\widehat{MBC}$

$\widehat{NBM}=\widehat{NMB} \Rightarrow$ Δ NBM cân tại N => BN = NM (đpcm)

Bài tập 4 trang 72 sgk Toán 8 tập 1 CTST

Cho tam giác ABC vuông tại A...

Hướng dẫn trả lời:

a) Xét ΔADB và ΔEDB có: 

Chung cạnh BD

$\widehat{DBA}=\widehat{DBE}$

AB = EB (gt)

 =>  ΔADB=ΔEDB (c.g.c).

b) ΔADB=ΔEDB

 => $\widehat{BAD}=\widehat{BED}=90^{\circ}$ => DE⊥BC

=> AH // DE ( cùng ⊥BC ) 

=> AHED là hình thang 

mà $\widehat{AHE}=90^{\circ}$ => AHED là hình thang vuông.

c) AB = EB (gt) => B nằm trên đường trung trực của AE.

ΔADB = ΔEDB => AD = ED => D nằm trên đường trung trực của AE.

BD là đường trung trực của đoạn thẳng AE =>  BD⊥AE 

Xét BAE có: BI⊥AE ; AI⊥BE => I là trực tâm của tam giác

EI⊥AB (EF⊥AB)

EF // AC ( cùng ⊥AB)

FEDA là hình thang; $\widehat{FAC}=90^{\circ}$ => FEDA là hình thang vuông.

Bài tập 5 trang 72 sgk Toán 8 tập 1 CTST

Tứ giác nào trong Hình 15 là hình thang cân...

Hướng dẫn trả lời:

Hình thang cân : MQPN ; DCBA

Bài tập 6 trang 72 sgk Toán 8 tập 1 CTST

Cho hình thang ABCD có...

Hướng dẫn trả lời:

Xét ΔADB và ΔBCA có: BD = AC ; AD = BC ; chung cạnh AB

ΔADB=ΔBCA (c.c.c) => $\widehat{B_1}= \widehat{A_1}$

FG // AB (gt) $\Rightarrow \widehat{A_1}= \widehat{E_1}; \widehat{B_1}= \widehat{E_2}$

$\widehat{E_1}= \widehat{E_2} \Rightarrow$ EG là tia phân giác của CEB(đpcm)

Bài tập 7 trang 72 sgk Toán 8 tập 1 CTST

Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang...

Hướng dẫn trả lời:

Kẻ BF⊥DC⇒BF=60cm

Δ vuông AED có:

$DE =\sqrt{AD^{2}-AE^{2}} = \sqrt{61^{2}-60^{2}} = 11(cm)$ 

Δ vuông BFC có:

$FC =\sqrt{BC^{2}-BF^{2}} = \sqrt{61^{2}-60^{2}} = 11(cm)$ 

$=>EF=DC-DE-FC =92-2.11=70(cm) = AB$