Tải giáo án điện tử dạy thêm Toán 11 KNTT Bài 27: Thể tích

CHÀO MỪNG CÁC EM  
ĐẾN VỚI TIẾT HỌC MÔN TOÁN! 

CHƯƠNG VII: QUAN HỆ  

VUÔNG GÓC TRONG KHÔNG GIAN 

BÀI 27: THỂ TÍCH 

HỆ THỐNG  
KIẾN THỨC 

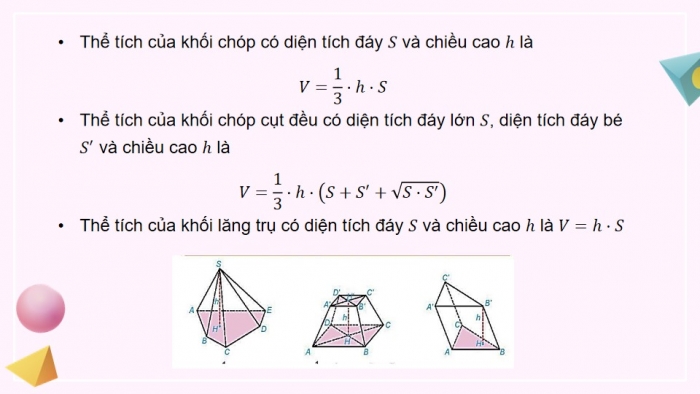
1. Thể tích khối chóp

Phần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khôi chóp, khối chóp cụt đều, khới lăng trụ, khối hộp. Đỉnh, mặt, cạnh, đường cao của các khối hình đó lần lượt là đỉnh, mặt, cạnh, đường cao của hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng. 

Thể tích của khối chóp có diện tích đáy S và chiều cao ℎ là  

V=1/3⋅ℎ⋅S 

Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đáy bé S^′ và chiều cao ℎ là  

V=1/3⋅ℎ⋅(S+S^′+√S⋅S^′) 

Thể tích của khối lăng trụ có diện tích đáy S và chiều cao ℎ là V=ℎ⋅S 

LUYỆN  
TẬP 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Thể tích khối chóp 

Phương pháp giải:  

Thể tích của khối chóp có diện tích đáy S và chiều cao ℎ là V=1/3⋅ℎ⋅S 

Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đáy bé S^′ và chiều cao ℎ là V=1/3⋅ℎ⋅(S+S^′+√S⋅S^′) 

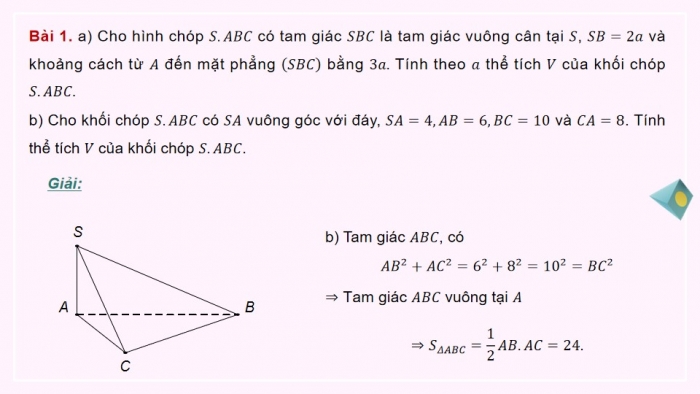
Bài 1. a) Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, SB=2a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC. 

8. b) Cho khối chóp S.ABC có SA vuông góc với đáy, SA=4,AB=6,BC=10 và CA=8. Tính thể tích V của khối chóp S.ABC.

Giải: 

1. a) Ta chọn (SBC) làm mặt đáy

⇒ chiều cao khối chóp là d[A,(SBC)]=3a 

Tam giác SBC vuông cân tại S nên S_ΔSBC=1/2SB^2=2a^2 

Vậy thể tích khối chóp V=1/3S_ΔSBC.d[A,(SBC)]=2a^3. 

1. b) Tam giác ABC, có

AB^2+AC^2=6^2+8^2=10^2=BC^2 

⇒ Tam giác ABC vuông tại A 

⇒S_ΔABC=1/2AB.AC=24. 

Bài 2. Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a√21/6. Tính theo a thể tích V của khối chóp đã cho. 

Giải: 

Gọi I là tâm đường tròn ngoại tiếp tam giác ABC  

Vì S.ABC là khối chóp đều nên suy ra SI⊥(ABC) 

Gọi M là trung điểm của BC⇒AI=2/3AM=a√3/3 

Tam giác SAI vuông tại I, có   

SI=√SA^2−AI^2√(a√21/6)^2−(a√3/3)^2=a/2  

Diện tích tam giác ABC là S_ΔABC=a^2√3/4 

Vậy thể tích khối chóp V_S.ABC=1/3S_ΔABC.SI=a^3√3/24. 

Bài 3. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60^0. Tính theo a thể tích V của khối chóp S.ABCD. 

Giải: 

Gọi O=AC∩BD 

Do S.ABCD là hình chóp đều nên SO⊥(ABCD) 

Suy ra OB là hình chiếu của SB trên (ABCD) 

Khi đó 60^0=(SB,(ABCD)) ̂=(SB,OB) ̂=(SBO) ̂ 

Tam giác vuông SOB, có  

SO=OB.tan(SBO) ̂=a√6/2  

Diện tích hình vuông ABC là S_ABCD=AB^2=a^2 

Vậy V_S.ABCD=1/3S_ABCD.SO=a^3√6/6. 

Bài 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; đỉnh S cách đều các điểm A, B, C. Biết AC=2a, BC=a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60^0. Tính theo a thể tích V của khối chóp S.ABC. 

Giải: 

Gọi H là trung điểm AC.  

Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.  

Đỉnh S cách đều các điểm A, B, C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC 

suy ra SH⊥(ABC) 

Do đó 60^0=(SB,(ABC)) ̂=(SB,BH) ̂=(SBH) ̂. 

Tam giác vuông SHB, có  

SH=BH.tan(SBH) ̂=AC/2.tan(SBH) ̂=a√3. 

Tam giác vuông ABC, có  

AB=√AC^2−BC^2=a√3. 

Diện tích tam giác vuông S_ΔABC=1/2BA.BC=a^2√3/2  

Vậy V_S.ABC=1/3S_ΔABC.SH=a^3/2. 

Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc 30^0. Tính theo a thể tích V của khối chóp S.ABCD. 

Giải: 

Gọi O=AC∩BD; M là trung điểm AB.  

Suy ra H=BO∩CM. 

Theo giả thiết SH⊥(ABCD) nên hình chiếu vuông góc của SD trên mặt đáy (ABCD) là HD.  

Do đó 30^0=(SD,(ABCD)) ̂=(SD,HD) ̂=(SDH) ̂. 

Tam giác ABC và ADC đều cạnh a, suy ra 

{█(OD=a√3/2@OH=1/3BO=a√3/6)┤⇒HD=OD+OH=2a√3/3  

Tam giác vuông SHD, có SH=HD.tan(SDH) ̂=2a/3 

Diện tích hình thoi S_ABCD=2S_ΔABC=2.a^2√3/4=a^2√3/2 

Vậy V_S.ABCD=1/3S_ABCD.SH=a^3√3/9. 

Bài 6. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2a. Mặt bên tạo với đáy góc 60^0. Gọi K là hình chiếu vuông góc của O trên SD. Tính theo a thể tích V của khối tứ diện DKAC. 

Giải: 

Gọi M là trung điểm CD, suy ra OM⊥CD nên  

60^0=((SCD),(ABCD)) ̂=(SM,OM) ̂=(SMO) ̂ 

Tam giác vuông SOM, có SO=OM.tan(SMO) ̂=a√3 

Kẻ KH⊥OD⇒KH∥SO nên KH⊥(ABCD) 

Tam giác vuông SOD, ta có 

KH/SO=DK/DS=DO^2/DS^2=OD^2/SO^2+OD^2=2/5⇒KH=2/5SO=2a√3/5  

Diện tích tam giác S_ΔADC=1/2AD.DC=2a^2 

Vậy V_DKAC=1/3S_ΔADC.KH=4a^3√3/15. 

Bài 7. Cho hình chóp S.ABC có (ASB) ̂=(CSB) ̂=60^0, (ASC) ̂=90^0 và SA=SB=a, SC=3a. Tính thể tích V của khối chóp S.ABC. 

...