Tải giáo án điện tử dạy thêm Toán 11 KNTT Bài tập cuối chương 9
Bài giảng điện tử hay còn gọi là giáo án điện tử powerpoint dạy thêm Toán 11 Kết nối tri thức Bài tập cuối chương 9. Bài soạn dạy thêm thiết kế đặc sắc, nhiều hình ảnh, video, trò chơi hấp dẫn. Bộ giáo án có file tải về và chỉnh sửa được. Mời thầy cô tham khảo chi tiết
Rõ nét về file powerpoint trình chiếu. => Xem thêm
CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY
CHƯƠNG IX: ĐẠO HÀM
BÀI TẬP CUỐI CHƯƠNG
PHIẾU BÀI TẬP SỐ 1
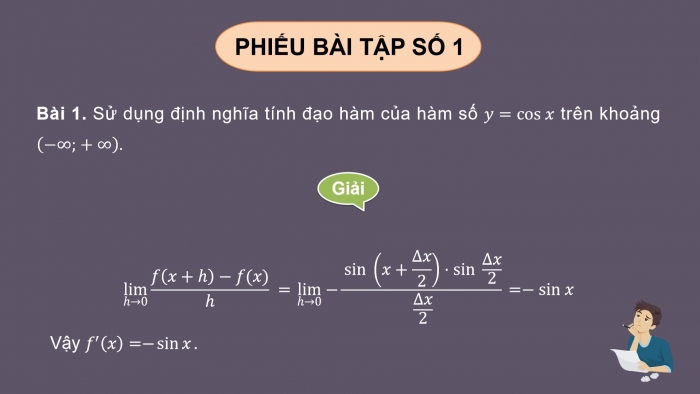
Bài 1. Sử dụng định nghĩa tính đạo hàm của hàm số y=cosx trên khoảng (−∞;+∞).
Giải
Ta có: f(x+h)−f(x)=cos(x+h)−cosx=−2sin(x+ℎ/2)⋅sinℎ/2
f(x+ℎ)−f(x)/ℎ=−2sin(x+ℎ/2)⋅sinℎ/2/ℎ=−sin(x+ℎ/2)⋅sinℎ/2/ℎ/2
lim┬ℎ→0f(x+ℎ)−f(x)/ℎ =lim┬ℎ→0 −sin(x+Δx/2)⋅sinΔx/2/Δx/2=−sinx
Vậy f^′(x)=−sinx.
Bài 2. Chứng minh rằng hàm số f(x)={■(cosx,&x≥0@−sinx,&x<0)□ ┤ không có đạo hàm tại x=0.
Giải
Ta có: lim┬x→0^+f(x)= lim┬x→0^+ cosx=1; lim┬x→0^− f(x)= lim┬x→0^−(−sinx)=0
⇒lim┬x→0^+ f(x)≠lim┬x→0^− f(x).
Suy ra hàm số gián đoạn tại x=0 nên không có đạo hàm tại đó.
Bài 3. Tìm a,b để hàm số f(x)={■(x^3/3& khi x>1@ax+b& khi x≤1)┤ có đạo hàm tại x=1.
Giải
Điều kiện cần
Ta có f(1)=1/3;lim┬x→1^+ f(x)=lim┬x→1^+ (x^3/3)=1/3 và lim┬x→1^− f(x)=lim┬x→1^−(ax+b)=a+b
Để hàm số f(x) có đạo hàm tại x=1 thì f(x) liên tục tại x=1
Do đó lim┬x→1^+ f(x)=lim┬x→1^− f(x)=f(1)⇔a+b=1/3.
Điều kiện đủ: lim┬x→1^+ f(x)−f(1)/x−1=lim┬x→1^+ x^3/3−1/3/x−1=lim┬x→1^+ x^2+x+1/3=1
lim┬x→1^− f(x)−f(1)/x−1=lim┬x→1^+ f(x)−f(1)/x−1=lim┬x→1^− ax+b−(a+b)/x−1=lim┬x→1^+ ax−a/x−1=a
Để hàm số f(x) có đạo hàm tại x=1 thì
lim┬x→1^+ f(x)−f(1)/x−1=lim┬x→1^− f(x)−f(1)/x−1⇔a=1⇒b=−2/3
Vậy a=1;b=−2/3 thỏa mãn yêu cầu của bài toán.
Bài 4. Tìm đạo hàm của các hàm số sau (giả sử các biểu thức có nghĩa):
- a) y=(1−√x/1+√x)^2
→y^′=2(1−√x/1+√x)(1−√x/1+√x)^′=2(1−√x/1+√x)−1/√x(1+√x)^2=−2/√x1−√x/(1+√x)^3
- b) y=(√x−1/√x)^2
→y^′=2(√x−1/√x).(1/2√x+1/2x√x)=1−1/x^2
Bài 5. Tìm đạo hàm của các hàm số sau (m là tham số), (giả sử các biểu thức có nghĩa):
- a) y=(2m+1)x−2(m+1)/mx+m^2−1
→y^′=[(2m+1)x−2(m+1)]^′⋅(mx+m^2−1)−(mx+m^2−1)^′⋅[(2m+1)x−2(m+1)]/(mx+m^2−1)^2
=(2m+1)⋅(mx+m^2−1)−m⋅[(2m+1)x−2(m+1)]/(mx+m^2−1)^2=2m^3+3m^2−1/(mx+m^2−1)^2
- b) y=x^2−2(m−1)x+m+3/x−1
→y^′=(x^2−2(m−1)x+m+3)^′(x−1)−(x−1)^′(x^2−2(m−1)x+m+3)/(x−1)^2
=(2x−2(m−1))(x−1)−(x^2−2(m−1)x+m+3)/(x−1)^2=x^2−2x+m−5/(x−1)^2
Bài 6. Tính đạo hàm của các hàm số sau (giả sử các biểu thức có nghĩa):
- a) y=1/(2x−5)^2
→y^′=−[(2x−5)^2]^′/(2x−5)^4=−2(2x−5)⋅(2x−5)′/(2x−5)^4=−4/(2x−5)^3
- b) y=4/(x^2−2x+5)^2
→y^′=−4⋅[(x^2−2x+5)^2]′/(x^2−2x+5)^4
=−4⋅2(x^2−2x+5)⋅(x^2−2x+5)′/(x^2−2x+5)^4=−16(x−1)/(x^2−2x+5)^3=16(1−x)/(x^2−2x+5)^3
- c) y=1/x−2/(3x−x^2)^5
→y^′=−1/x^2+2⋅[(3x−x^2)^5]^′/(3x−x^2)^10=−1/x^2+25(3x−x^2)^4⋅(3x−x^2)^′/(3x−x^2)^10
=├ 10(3−2x)/(3x−x^2)^6−1/x^2
Bài 7. Tính đạo hàm của hàm số (giả sử các biểu thức có nghĩa):
- a) y=3x^2−4√x+2/x−1
→y^′=6x−4⋅1/2√x−2⋅1/x^2=6x−2/√x−2/x^2
- b) y=√x^2+6x+7
→y^′=(x^2+6x+7)′/2√x^2+6x+7=2x+6/2√x^2+6x+7=x+3/√x^2+6x+7
PHIẾU BÀI TẬP SỐ 2
Bài 1. Cho hàm số y=sinx−xcosx/cosx+xsinx. Chứng minh rằng: y^′(sinx−xcosx)^2−x^2y^2=0.
Giải
y^′=(sinx−xcosx)^′(cosx+xsinx)−(sinx−xcosx)(cosx+xsinx)^′/(cosx+xsinx)^2
Ta có:
+) (sinx−xcosx)^′=cosx−x^′cosx−x⋅(cosx)^′=xsinx
+) (cosx+xsinx)^′=−sinx+x^′sinx+x⋅(sinx)^′=xcosx
Do đó: y^′=xsinx⋅(cosx+xsinx)−(sinx−xcosx)xcosx/(cosx+xsinx)^2=x^2/(cosx+xsinx)^2
Ta có: VT=y^′(sinx−xcosx)^2−x^2y^2
=x^2/(cosx+xsinx)^2⋅(sinx−xcosx)^2−x^2⋅(sinx−xcosx/cosx+xsinx)^2=0=VP
Vậy ta có điều phải chứng minh.
Bài 2. Giải phương trình f^′(x)=0 trong các trường hợp sau
- a) f(x)=sin3x−3sinx+7; b) f(x)=cos2x+2sinx−1.
Giải
- a) f(x)=sin3x−3sinx+7⇒f^′(x)=3cos3x−3cosx.
Khi đó: f^′(x)=0⇔3cos3x−3cosx=0⇔cos3x=cosx
⇔[■(3x=x+k2π@3x=−x+k2π)┤⇔[■(x=kπ@x=kπ/2)┤ (k∈ℤ)
- b) f(x)=cos2x+2sinx−1⇒f^′(x)=−2sin2x+2cosx.
f^′(x)=0⇔−2sin2x+2cosx=0⇔cosx(−2sinx+1)=0
⇔[■(cosx=0@sinx=1/2)┤⇔[■(x=π/2+kπ@x=π/6+k2π@x=π−π/6+k2π)┤⇔[■(x=π/2+kπ@x=π/6+k2π@x=5π/6+k2π)┤□ (k∈ℤ)
Bài 3. Cho hàm số f(x)=cos^2x/1+sin^2x⋅ Chứng minh f(π/4)−3⋅f^′(π/4)=3.
...
Hình ảnh về file sile, ppt trình chiếu











.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Giáo án dạy thêm Powerpoint Toán11 kết nối, Tải giáo án điện tử dạy thêm Toán 11 kết nối tri thức, giáo án powerpoint tăng cường Toán 11 Kết nối Bài tập cuối chương 9
