Tải giáo án điện tử dạy thêm Toán 8 KNTT Bài 35: Định lí Pythagore và ứng dụng

KÍNH CHÀO QUÝ THẦY CÔ VÀ CÁC BẠN ĐẾN VỚI BUỔI HỌC HÔM NAY 

BÀI 35. ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Áp dụng định lí Pythagore (pytago) để tính theo yêu cầu bài toán 

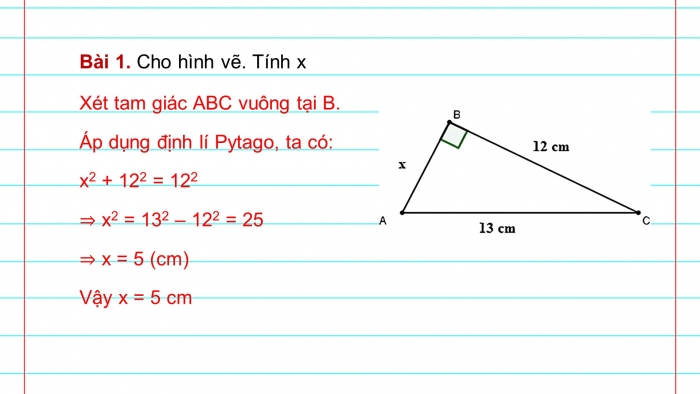
Bài 1. Cho hình vẽ. Tính x 

Xét tam giác ABC vuông tại B.  

Áp dụng định lí Pytago, ta có: 

x2 + 122 = 122 

⇒ x2 = 132 – 122 = 25 

⇒ x = 5 (cm) 

Vậy x = 5 cm 

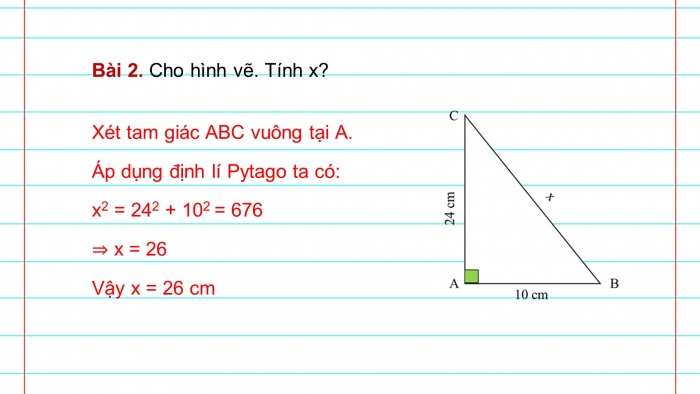
Bài 2. Cho hình vẽ. Tính x? 

Xét tam giác ABC vuông tại A.  

Áp dụng định lí Pytago ta có: 

x2 = 242 + 102 = 676 

⇒ x = 26 

Vậy x = 26 cm 

Bài 3. Cho hình vẽ sau. Tìm x 

DADE vuông tại A.  

Áp dụng định lý Py-ta-go, ta có: 

AD^2+AE^2=DE^2 

⇔3^2+AE^2=5^2 

⇔AE=4  

Từ đó: Suy ra AB = 8 

DABC vuông tại A. Áp dụng định lý Py-ta-go, ta có: 

AB^2+AC^2=BC^2⇔8^2+6^2=BC^2⇔BC=10 (đvđd) 

Bài 4. Cho ∆ABC vuông tại A. Biết 3AB = 4AC và BC = 20cm. Tính độ dài các cạnh AB và AC 

∆ABC vuông tại A. Áp dụng định lí Pytago, ta có: 

AB^2+AC^2=BC^2⇔AB^2+AC^2=400 

Từ đề bài: 3AB=4AC⇔AB/4=AC/3⇔AB^2/16=(AC^2)/9 

Áp dụng dãy tỉ số bằng nhau: 

(AB^2+AC^2)/(16+9)=400/25=16 

→AB=16cm→AC=12cm 

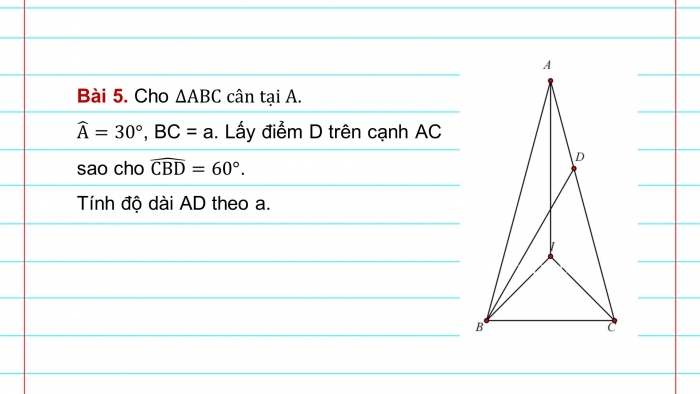
Bài 5. Cho ∆ABC cân tại A. 

A ̂=30°, BC = a. Lấy điểm D trên cạnh AC sao cho (CBD) ̂=60°.  

Tính độ dài AD theo a. 

∆ABC cân tại A; A ̂=30° nên (ABC) ̂=(ACB) ̂=75°. Trên nửa măt phẳng bờ BC, chứa điểm A vẽ ∆BIC cân tại I thì I nằm trong ∆ABC. Ta có: 

(CBI) ̂=45° ;(IBA) ̂=30°→(IBD) ̂=15°→(ABD) ̂=15° 

∆IAB và ∆IAC có:AB=AC;IB=IC, AI chung. 

=> ∆IAB=∆IAC (c.c.c) 

=> (IAB) ̂=(IAC) ̂=15° 

∆IAB và ∆DBA có (IAB) ̂=(DBA) ̂;AB chung;(ABI) ̂=(BAD) ̂ 

=> ∆IAB= ∆DBA (g.c.g)=>IB=AD  

∆IBC vuông cân tại I, theo Pytago có: 

BI^2+IC^2=BC^2=a^2→2. BI^2=a^2→BI=a/√2     

Bài 6. Hình thang vuông ABCD có A ̂=D ̂=90°, AB = 9 cm, AC = 17 cm. Tính độ dài các cạnh bên. 

Tam giác ADC vuông tại D ,  

theo định lí pytago ta có: AC^2=AD^2+DC^2 

→AD^2=AC^2-CD^2=〖17〗^2-〖15〗^2=8^2.  

Vậy AD = 8cm 

Kẻ BH⊥CD. Hình thang ABHD có AD // BH, nên: 

BH = AD = 8 cm; DH = AB = 9 cm => HC = 15 – 9 = 6 cm 

∆BHC vuông tại H, theo định lí Pytago: BC^2=BH^2+HC^2=8^2+6^2=〖10〗^2 

Vậy BC = 10 cm. 

PHIẾU BÀI TẬP SỐ 2 

DẠNG 2: Sử dụng định lý Pythagore (pytago) vào những bài tập chứng minh, tính toán có tính chất tổng hợp, phức tạp. 

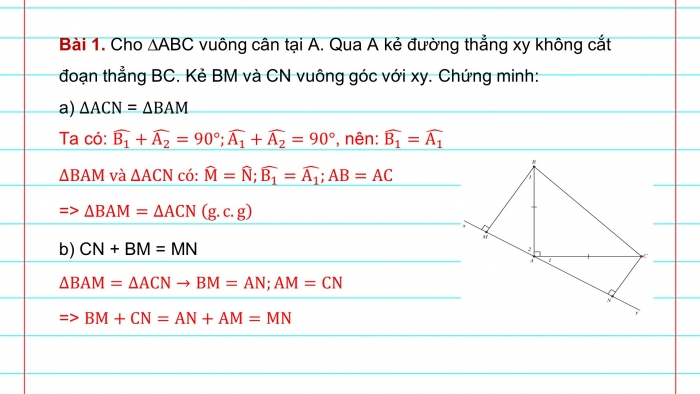
Bài 1. Cho DABC vuông cân tại A. Qua A kẻ đường thẳng xy không cắt đoạn thẳng BC. Kẻ BM và CN vuông góc với xy. Chứng minh: 

1. a) ∆ACN = ∆BAM

Ta có: (B_1 ) ̂+(A_2 ) ̂=90°;(A_1 ) ̂+(A_2 ) ̂=90°, nên: (B_1 ) ̂=(A_1 ) ̂ 

∆BAM và ∆ACN có: M ̂=N ̂;(B_1 ) ̂=(A_1 ) ̂;AB=AC  

=> ∆BAM=∆ACN (g.c.g)  

1. b) CN + BM = MN

∆BAM=∆ACN→BM=AN;AM=CN 

=> BM+CN=AN+AM=MN 

1. c) BM2 + CN2 không phụ thuộc vào vị trí xy

Áp dụng định lí Pytago cho ∆BAM vuông: 

BM^2+AM^2=AB^2 hay BM^2+CN^2=AB^2 

=> BM^2+CN^2 không phụ thuộc vào vị trí của xy 

1. d) Tìm điều kiện của xy để A là trung điểm của MN

∆BAM=∆ACN→AM=CN 

AM=AN→AN=CN hay ∆ACN vuông cân tại N 

⇔ (A_1 ) ̂=45°⇔ xy // BC 

Bài 2. Cho ∆ABC có A ̂=50°;B ̂=20°. Trên đường phân giác BE của góc ABC lấy F sao cho: (FAB) ̂=20°. Gọi I là trung điểm của AF, K là giao điểm của tia EI với AB, M là giáo điểm của CK với EB.  

Chứng minh: AI^2+EI^2=AF.(MF+1/2 KE) 

Bài 2. 

∆ABF có:(AFE) ̂=(BAF) ̂+(ABF) ̂=30°  

(tính chất góc ngoài tam giác)  

Suy ra (EAF) ̂=(EFA) ̂→∆EAF cân tại E 

→EA=EF 

∆EAI và ∆EFI có:IA=IF;EA=EF; 

EI chung  

=> ∆EAI=∆EFI (c.c.c) 

=> (AEI) ̂=(FEI) ̂;(AIE) ̂=(FIE) ̂=90° 

→(AEI) ̂=(FEI) ̂=1/2 (AEF) ̂=60° 

Từ đó suy ra: 

∆CEB=∆KEB (g.c.g)  

=> EC=EK;BC=BK;(BEC) ̂=(BEK) ̂=60° 

=> ∆EKM=∆ECM (c.g.c) 

=> (EMK) ̂=(EMC) ̂=90° 

=> EM=1/2 EK 

∆AIE vuông tại I suy ra: 

AI^2+EI^2=AE^2=AE.EF 

=AE.(MF+EM)=AE.(MF+1/2 EK) 

Bài 3. Cho ∆ABC có M là trung điểm của cạnh BC. Biết AB = 2cm, AC = 4cm và AM = √3  cm. Hãy tính số đo góc BAC và độ dài BC? 

Bài 3. 

Trên tia AM lấy điểm D sao cho M là trung điểm của AD -> AD = 2√3 cm 

∆AMB và ∆DMC có: 

MB = MC, (AMB) ̂ = (DMC) ̂, MA = MD 

Þ∆AMB = ∆DMC (c.g.c) 

ÞAB = DC = 2cm 

Xét ∆ADC có: 

DC2 + AD2 = 22 + (2√3)2 = 16; 

AC2 = 16 -> DC2 + AD2 = AC2 

=> ∆ADC vuông tại D (định lí Pytago) 

Þ(MDC) ̂ = 90° => (MBA) ̂ = 90° 

Gọi E là trung điểm của AC  

-> DE = 2 cm = CE = DC 

=> ∆DCE là tam giác đều 

=> (DCI) ̂ = 60° -> (MAC) ̂ = 30° -> (BAC) ̂ = 120° 

∆ABM vuông tại A nên 

MB2 = AB2 + AM2 = 22 + (√3)2 = 7 

=> MB = √7 cm -> BC = 2√7 cm 

Bài 4. Cho DABC vuông tại A. Lấy D là trung điểm của AB. Từ D kẻ DE vuông góc với BC. Chứng minh rằng: EC2 – EB2 = AC2 

...