Tải giáo án điện tử dạy thêm Toán 8 KNTT Bài 39: Hình chóp tứ giác đều

THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI 

BÀI 39.  

HÌNH CHÓP TỨ GIÁC ĐỀU 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Nhận biết các kiến thức căn bản về hình chóp tứ giác đều 

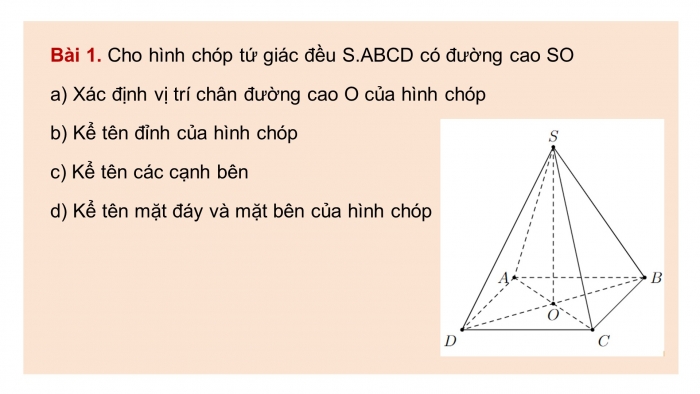
Bài 1. Cho hình chóp tứ giác đều S.ABCD có đường cao SO 

1. a) Xác định vị trí chân đường cao O của hình chóp
2. b) Kể tên đỉnh của hình chóp
3. c) Kể tên các cạnh bên
4. d) Kể tên mặt đáy và mặt bên của hình chóp
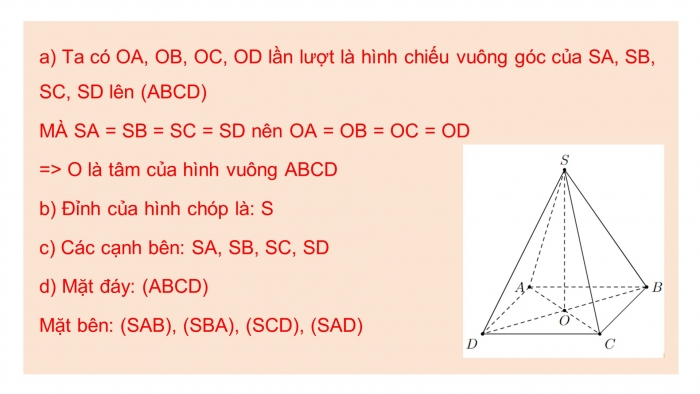
5. a) Ta có OA, OB, OC, OD lần lượt là hình chiếu vuông góc của SA, SB, SC, SD lên (ABCD)

MÀ SA = SB = SC = SD nên OA = OB = OC = OD 

=> O là tâm của hình vuông ABCD 

1. b) Đỉnh của hình chóp là: S
2. c) Các cạnh bên: SA, SB, SC, SD
3. d) Mặt đáy: (ABCD)

Mặt bên: (SAB), (SBA), (SCD), (SAD) 

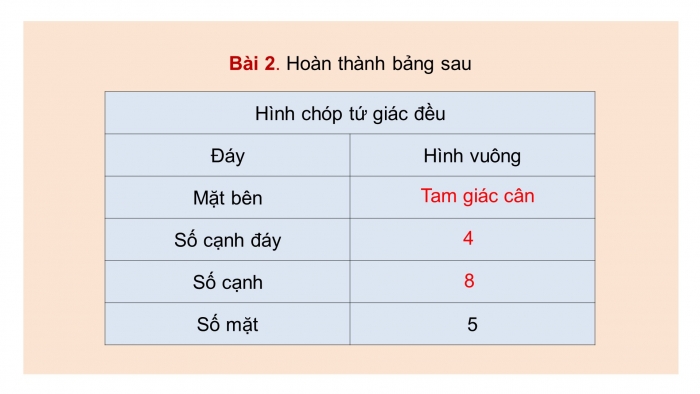
Bài 2. Hoàn thành bảng sau 

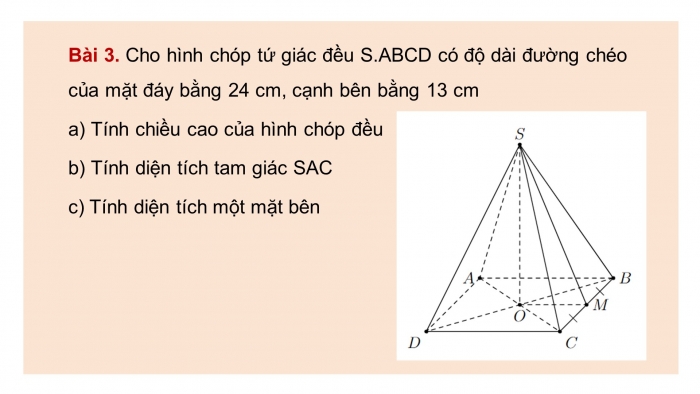
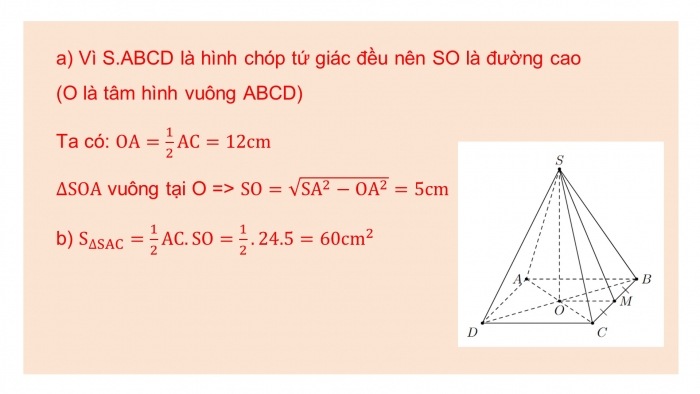
Bài 3. Cho hình chóp tứ giác đều S.ABCD có độ dài đường chéo của mặt đáy bằng 24 cm, cạnh bên bằng 13 cm 

1. a) Tính chiều cao của hình chóp đều
2. b) Tính diện tích tam giác SAC
3. c) Tính diện tích một mặt bên
4. a) Vì S.ABCD là hình chóp tứ giác đều nên SO là đường cao (O là tâm hình vuông ABCD)

Ta có: OA=1/2 AC=12cm 

∆SOA vuông tại O => SO=√(SA^2-OA^2 )=5cm 

2. b) S_∆SAC=1/2 AC.SO=1/2.24.5=60cm^
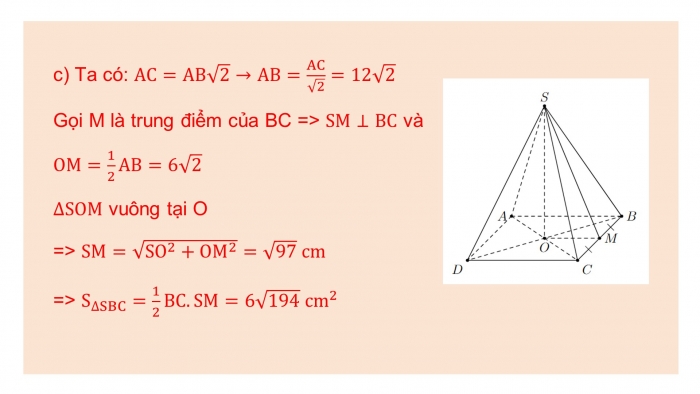
3. c) Ta có: AC=AB√2→AB=AC/√2=12√2

Gọi M là trung điểm của BC => SM⊥BC và OM=1/2 AB=6√2 

∆SOM vuông tại O  

=> SM=√(SO^2+OM^2 )=√97  cm 

=> S_∆SBC=1/2 BC.SM=6√194  cm^2 

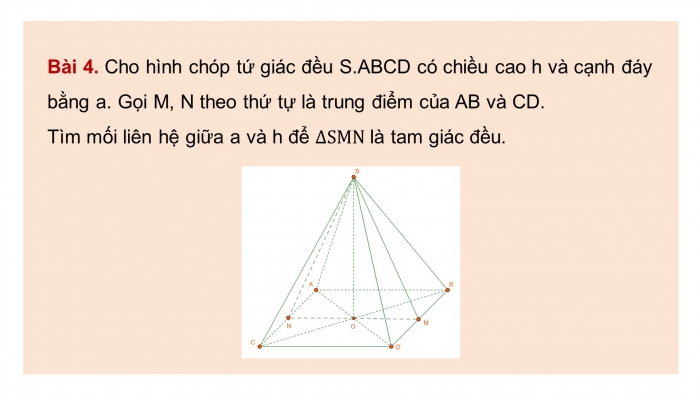
Bài 4. Cho hình chóp tứ giác đều S.ABCD có chiều cao h và cạnh đáy bằng a. Gọi M, N theo thứ tự là trung điểm của AB và CD.  

Tìm mối liên hệ giữa a và h để ∆SMN là tam giác đều. 

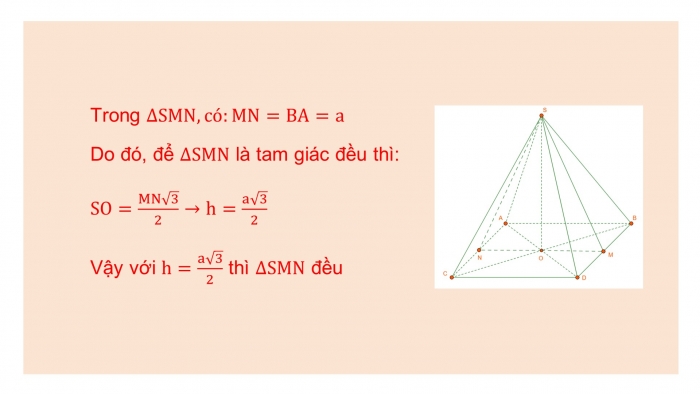
Trong ∆SMN, có:MN=BA=a 

Do đó, để ∆SMN là tam giác đều thì: 

SO=(MN√3)/2→h=(a√3)/2  

Vậy với h=(a√3)/2 thì ∆SMN đều 

PHIẾU BÀI TẬP SỐ 2 

DẠNG 2: Diện tích xung quanh và thể tích của hình chóp đều 

Bài 1. Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng 5dm, cạnh đáy bằng 6dm. 

1. a) Xác định vị trí chân đường cao H của hình chóp đều và tính SH?
2. b) Tính diện tích xung quanh hình chóp đều
3. c) Tính thể tích hình chóp đều
4. a) Xác định vị trí chân đường cao H của hình chóp đều và tính SH?

Chân đường cao của hình chóp là tâm H của hình vuông ABCD. 

Gọi M là trung điểm của BC => SM là trung đoạn của hình chóp. 

∆SMC vuông tại M  

=> SM=√(SC^2-MC^2 )=4dm 

∆SHM vuông tại H  

=> SH=√(SM^2-HM^2 )=√(SM^2-(AB^2)/4)=√5  dm 

1. b) Tính diện tích xung quanh hình chóp đều

S_xq = (AB + BC) . SM = 48 dm2  

1. c) Tính thể tích hình chóp đều

V = 1/3 . SH . AB . AD = 12√5 dm3 

Bài 2. Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD có SH = 20cm; BC = 20cm. 

Diện tích xung quanh của  

hình chóp tứ giác đều S.ABCD: 

Sxq  = 2 . BC . SH = 800 cm2 

Bài 3. Kim tự tháp Kheops ở Ai Cập có hình dạng là một hình chóp tứ giác đều, chiều cao kim tự tháp là 137m, cạnh đáy dài 231m. Tính diện tích xung quanh và thể tích của kim tự tháp. 

Coi kim tự tháp là hình chóp S.ABCD có đường cao SO.  

Ta có: OM=1/2  AB=115,5 m  

∆SOM vuông tại O => SM=√(SO^2+OM^2 )=√128437/2  m 

Diện tích xung quanh của kim tự tháp là: 

S_xq=2.AB.SM=231.√128437  m^2  

Thể tích của kim tự tháp là V=1/3 SO.AB^2=2436819 m^3 

Bài 4. Cho hình lập phương ABCD.A’B’C’D’ cạnh a.  

Gọi O là tâm mặt đáy ABCD. 

1. a) CHứng minh O.A’B’C’D’ là hình chóp tứ giác đều
2. b) Gọi thể tích hình lập phương là V, thể tích hình chóp đều O.A’B’C’D’ là V’. Tính tỉ số V/V^′

...