Tải giáo án điện tử dạy thêm Toán 8 KNTT Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

CHÀO CẢ LỚP! CHÀO MỪNG CÁC EM TỚI BUỔI HỌC NÀY 

Bài 36. 

CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC VUÔNG 

PHIẾU BÀI TẬP SỐ 1 

Dạng 1: SỬ DỤNG  

TRƯỜNG HỢP ĐỒNG DẠNG  

GÓC - GÓC 

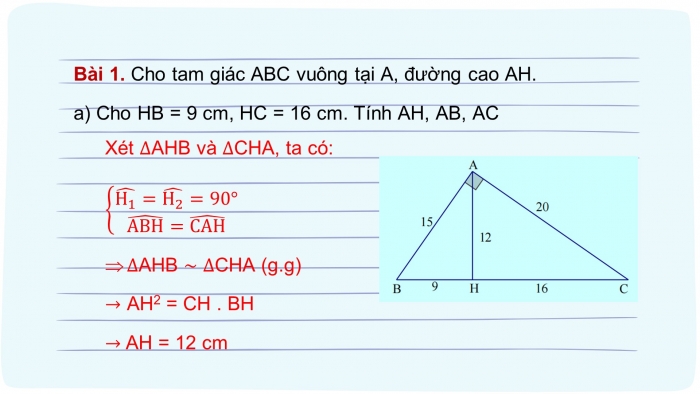
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. 

1. a) Cho HB = 9 cm, HC = 16 cm. Tính AH, AB, AC

Xét ∆AHB và ∆CHA, ta có:   {█((H_1 ) ̂=(H_2 ) ̂=90°@(ABH) ̂=(CAH) ̂ )┤  

Þ∆AHB ~ ∆CHA (g.g) 

→ AH2 = CH . BH 

→ AH = 12 cm 

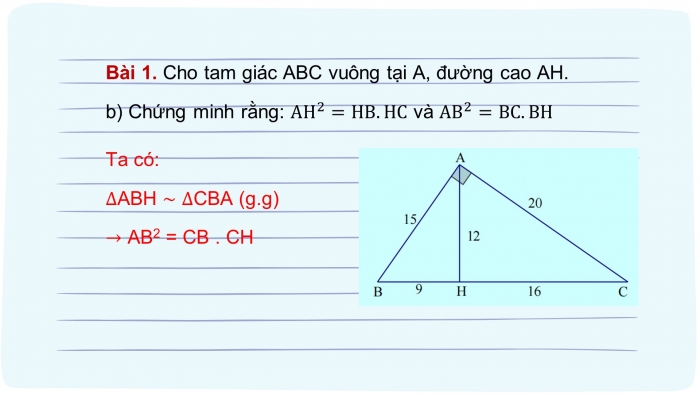
1. b) Chứng minh rằng: AH^2=HB.HC và AB^2=BC.BH

Ta có:  

∆ABH ~ ∆CBA (g.g) 

→ AB2 = CB . CH 

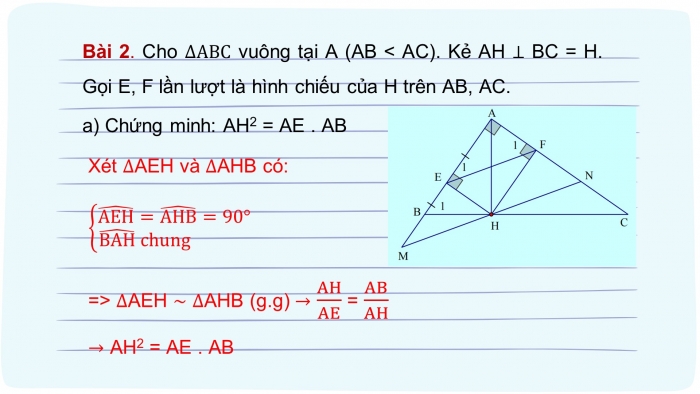
Bài 2. Cho ∆ABC vuông tại A (AB < AC). Kẻ AH ⊥ BC = H. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. 

1. a) Chứng minh: AH2 = AE . AB

Xét ∆AEH và ∆AHB có:  {█((AEH) ̂=(AHB) ̂=90°@(BAH) ̂  chung              )┤   

=> ∆AEH ~ ∆AHB (g.g) → AH/AE = AB/AH 

→ AH2 = AE . AB 

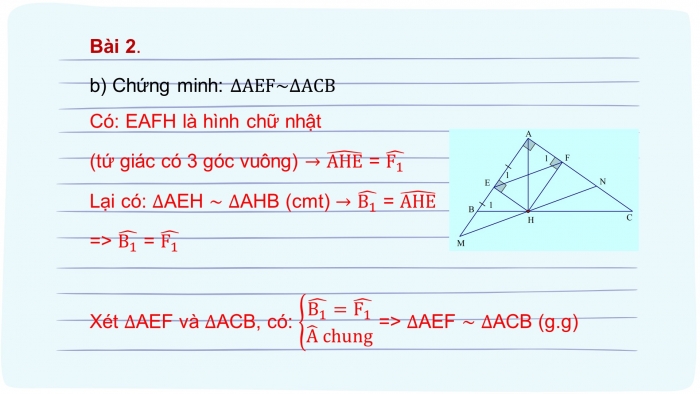
1. b) Chứng minh: ∆AEF~∆ACB

Có: EAFH là hình chữ nhật  

(tứ giác có 3 góc vuông) → (AHE) ̂ = (F_1 ) ̂ 

Lại có: ∆AEH ~ ∆AHB (cmt) → (B_1 ) ̂ = (AHE) ̂ 

=> (B_1 ) ̂ = (F_1 ) ̂ 

Xét ∆AEF và ∆ACB, có: {█((B_1 ) ̂=(F_1 ) ̂@A ̂  chung)┤ => ∆AEF ~ ∆ACB (g.g) 

1. c) Lấy M đối xứng với A qua E, tia NH cắt cạnh AC tại N.

Chứng minh: (ABH) ̂=(ANH) ̂ và EF // HN 

Ta có: (HMA) ̂ = (BAH) ̂ = (ACB) ̂ → ∆ABC ~ ∆ANB (g.g) 

=> (ABH) ̂ = (ANH) ̂ 

Do (AFE) ̂ = (ANH) ̂ = (ABH) ̂ → EF // MN 

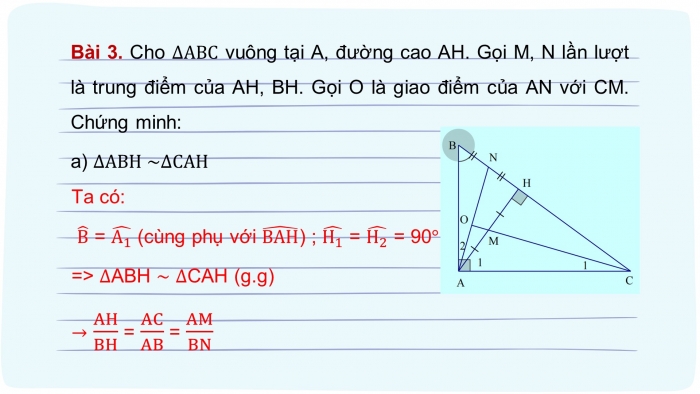
Bài 3. Cho ∆ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là trung điểm của AH, BH. Gọi O là giao điểm của AN với CM. Chứng minh: 

1. a) ∆ABH ~∆CAH

Ta có: 

 B ̂ = (A_1 ) ̂ (cùng phụ với (BAH) ̂) ; (H_1 ) ̂ = (H_2 ) ̂ = 90° 

=> ∆ABH ~ ∆CAH (g.g) 

→ AH/BH = AC/AB = AM/BN 

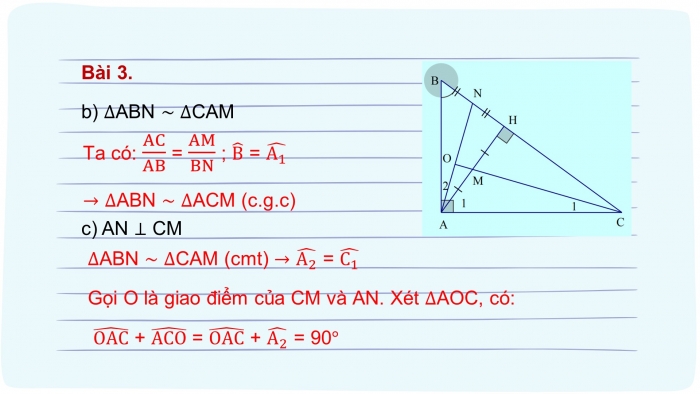
1. b) ∆ABN ~ ∆CAM

Ta có: AC/AB = AM/BN ; B ̂ = (A_1 ) ̂ 

→ ∆ABN ~ ∆ACM (c.g.c) 

1. c) AN ⊥ CM

∆ABN ~ ∆CAM (cmt) → (A_2 ) ̂ = (C_1 ) ̂  

Gọi O là giao điểm của CM và AN. Xét ∆AOC, có: 

 (OAC) ̂ + (ACO) ̂ = (OAC) ̂ + (A_2 ) ̂ = 90° 

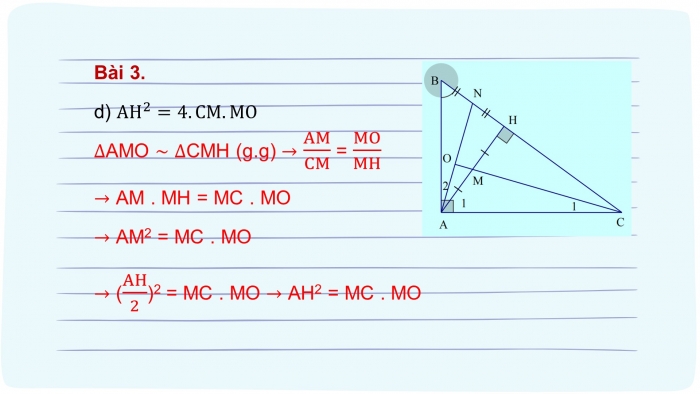
4. d) AH^2=4.CM.MO

∆AMO ~ ∆CMH (g.g) → AM/CM = MO/MH 

→ AM . MH = MC . MO  

→ AM2 = MC . MO 

→ (AH/2)2 = MC . MO → AH2 = MC . MO 

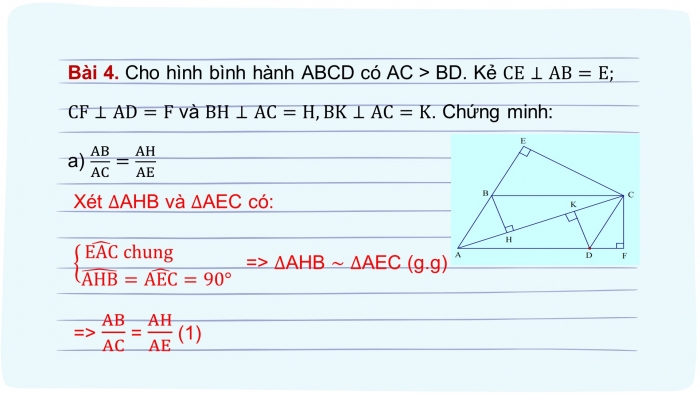
Bài 4. Cho hình bình hành ABCD có AC > BD. Kẻ CE⊥AB=E;  

CF⊥AD=F và BH⊥AC=H, BK⊥AC=K. Chứng minh: 

1. a) AB/AC=AH/AE

Xét ∆AHB và ∆AEC có:   

{█((EAC) ̂  chung             @(AHB) ̂=(AEC) ̂=90°)  ┤ => ∆AHB ~ ∆AEC (g.g) 

=> AB/AC = AH/AE (1) 

1. b) AD . AF = AK . AC

Tương tự ta có: ∆AKD ~ ∆AFC (g.g)  

à AD . AF = AK . AC (2) 

1. c) AD . AF + AB . AE = AC2

Từ (1)(2) suy ra: AB . AE = AC . AH (3) 

Lấy (2) + (3) ta được: AD . AF + AB . AE = AC2 (đpcm) 

PHIẾU BÀI TẬP SỐ 2 

Dạng 2: SỬ DỤNG  

TRƯỜNG HỢP ĐỒNG DẠNG  

C-G-C VÀ CẠNH HUYỀN- CẠNH GÓC VUÔNG 

Bài 1. Cho hình chữ nhật ABCD. Kẻ DE vuông góc với AC tại E. Gọi M, N, P lần lượt là trung điểm của BC, AE và DE.  

Chứng minh: 

1. a) AD/DC=AE/DE

Xét ∆AED và ∆ACD, có: 

{█(A ̂  chung                   @(AED) ̂=(ADC) ̂=90°)┤ => ∆ADE ~ ∆ACD (g.g) 

1. b) ∆AND ~ ∆DPC

Ta có: ∆ADE ~ ∆ACD → AE/AD = DE/CD → AE/DE = AD/DC = AN/DP 

Chứng minh được: ∆AND ~ ∆DNC (c.g.c)  

1. c) ND⊥NM

P là trục tâm của ∆CDN → CP ⊥ DN (1) 

Tứ giác MNPC là hình bình hành => MN // PC (2) 

Từ (1)(2) => MN ⊥ DN 

Bài 2. Cho ∆ABC cân tại A, gọi H là trung điểm của BC. Vẽ HE vuông góc với AC, gọi O là trung điểm của HE. Vẽ BK vuông góc với AC, BE cắt AO tại I. 

1. a) Chứng minh: ∆AHE ~ ∆BCK

Xét ∆AHE và ∆BCK có:  

(AEH) ̂ = (BKC) ̂ = 90° ; (HAE) ̂ = (CBK) ̂ 

→ ∆AHE ~ ∆BCK (g.g) 

1. b) Chứng minh: AE . EK = BK . OE

Ta có: ∆AHE ~ ∆BCK (g.g) → AE/BK = HE/CK = OE/EK 

→ AE/EO = BK/KE → ∆AEO ~ ∆BKE (c.g.c)  

1. c) Chứng minh: OA ⊥ BE

Theo câu b, có: 

∆AEO ~ ∆BKE (c.g.c) → (EBK) ̂ = (EAI) ̂ ; (KBE) ̂ + (EBK) ̂ = 90° 

→ (KEB) ̂ + (EAI) ̂ = 90° 

Bài 3. Cho tam giác ABC, trực tâm H. Gọi M, N lần lượt là trung điểm của BC và AC. Gọi O là giao điểm của các đường trung trực của tam giác, G là trọng tâm ∆ABC. Chứng minh: 

1. a) ∆OMN ~ ∆HAB để suy ra AH = 2 . OM

...