Tải giáo án điện tử dạy thêm Toán 11 cánh diều Chương 8 Bài 1: Hai đường thẳng vuông góc

CHÀO MỪNG CÁC EM 
ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

KHỞI ĐỘNG

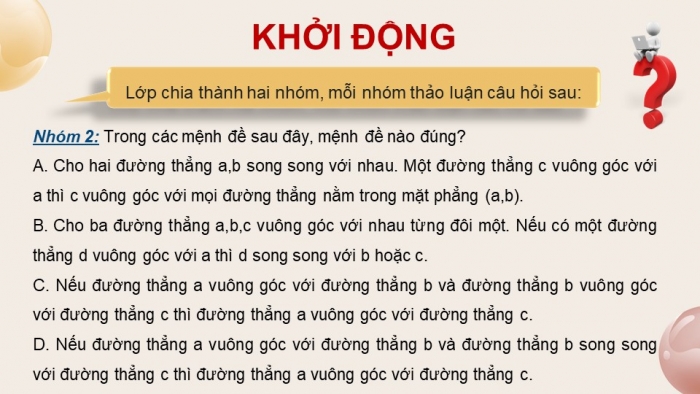
Lớp chia thành hai nhóm, mỗi nhóm thảo luận câu hỏi sau:

Nhóm 1: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c.         

B. Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng SA vuông góc với a thì d song song với b hoặc c.

C. Nếu đường thẳng O vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng BD thì a vuông góc với c.

D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong.

Nhóm 2: Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Cho hai đường thẳng a,b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a,b).              

B. Cho ba đường thẳng a,b,c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c.

C. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì đường thẳng a vuông góc với đường thẳng c.          

D. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì đường thẳng a vuông góc với đường thẳng c.

CHƯƠNG VIII. QUAN HỆ

VUÔNG GÓC TRONG KHÔNG GIAN. PHÉP CHIẾU VUÔNG GÓC

BÀI 1: HAI ĐƯỜNG THẲNG VUÔNG GÓC

HỆ THỐNG KIẾN THỨC

1. Góc giữa hai đường thẳng trong không gian

Góc giữa hai đường thẳng và  trong không gian là góc giữa hai đường thẳng  và  cùng đi qua một điểm  và lần lượt song song (hoặc trùng) với và , kí hiệu  hoặc

•       Nhận xét:

 - Góc giữa hai đường thẳng  không phụ thuộc vào vị trí điểm . Thông thường, khi tìm góc giữa đường thẳng  ta chọn  thuộc  hoặc  thuộc .

 - Góc giữa đường thẳng  bằng góc giữa hai đường thẳng  tức là

 - Góc giữa hai đường thẳng không vượt quá .

 - Nếu  thì  với mọi đường thẳng  trong không gian.

2. Hai đường thẳng vuông góc trong không gian

Hai đường thẳng được gọi là vuông góc với nhay nếu góc giữa chúng bằng .

•       Nhận xét:

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại.

LUYỆN TẬP

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Tính góc giữa hai đường thẳng

Phương pháp giải:

Cách 1.Tìm góc giữa hai đường thẳng  bằng cách chọn một điểm  thích hợp (thường nằm trên một trong hai đường thẳng).

Từ  dựng các đường thẳng   lần lượt song song (có thể trùng nếu  nằm trên một trong hai đường thẳng) với  và . Góc giữa hai đường thẳng  chính là góc giữa hai đường thẳng .

Lưu ý: Để tính góc này ta thường sử dụng định lí côsin trong tam giác .

Phương pháp giải:

Cách 2. Tìm hai vec tơ chỉ phương  của hai đường thẳng

Lưu ý: Để tính ta chọn ba vec tơ không đồng phẳng mà có thể tính được độ dài và góc giữa chúng, sau đó biểu thị các vec tơ qua các vec tơ rồi thực hiện các tính toán.

 là?

Giải

Gọi ,  lần lượt là trung điểm ,

Ta có:

Gọi  là giao điểm của  và

Ta có:

Xét  vuông tại , ta có:

Mà: .

Bài 2. Cho hình hộp . Giả sử tam giác  và  đều có 3 góc nhọn. Góc giữa hai đường thẳng  và  là góc nào?

Giải:

Ta có:  (tính chất của hình hộp)

 (do giả thiết cho  nhọn).

Bài 3. Cho tứ diện đều  (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng  và  bằng?

Giải

Gọi  là tâm đường tròn ngoại tiếp

Gọi  là trung điểm   (do  đều)

Do

Ta có:

.

Bài 4. Cho tứ diện đều ,  là trung điểm của cạnh . Khi đó  bằng?

Giải:

Không mất tính tổng quát, giả sử tứ diện  có cạnh bằng .

Gọi  là tâm đường tròn ngoại tiếp

Gọi  là trung điểm  

Ta có:

Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của :