Tải giáo án điện tử dạy thêm Toán 11 cánh diều Chương 2 Bài 1: Dãy số

THÂN MẾN CHÀO ĐÓN CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

+ Cách xác định một dãy số? + Cách xác định một dãy số?

+ Cho dãy số  + Cho dãy số . Tìm 5 số hạng đầu tiên của dãy số?

CHƯƠNG II: DÃY SỐ.

CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN

BÀI 1. DÃY SỐ

HỆ THỐNG KIẾN THỨC

1. Khái niệm

a) Khái niệm

- Mỗi hàm số u: {1; 2; 3; …; m} → ℝ  được gọi là một dãy số hữu hạn.

Do mỗi số nguyên dương  tương ứng với đúng mọi số  nên ta có thể viết dãy số đó dưới dạng khai triển: .

- Số  gọi là số hạng đầu, số  gọi là số hạng cuối của dãy số đó.

b) Khái niệm về sãy số vô hạn (dãy số):

- Mỗi hàm số  được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương n tương ứng với đúng một số  nên ta có thể viết dãy số đó dưới dạng khai triển:

- Dãy số đó còn được viết tắt là

- Số  gọi là số hạng thứ nhất (hay số hạng đầu), số  gọi là số hạng thứ hai,…, số  gọi là số hạng thứ n và là số hạng tổng quát của dãy số đó.

b) Khái niệm về sãy số vô hạn (dãy số):

- Mỗi hàm số  được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương n tương ứng với đúng một số  nên ta có thể viết dãy số đó dưới dạng khai triển:

- Dãy số đó còn được viết tắt là

- Số  gọi là số hạng thứ nhất (hay số hạng đầu), số  gọi là số hạng thứ hai,…, số  gọi là số hạng thứ n và là số hạng tổng quát của dãy số đó.

3. Dãy số tăng, dãy số giảm

- Dãy số  được gọi là dãy số tăng

nếu  với mọi .

 - Dãy số  được gọi là dãy số giảm

nếu  với mọi .

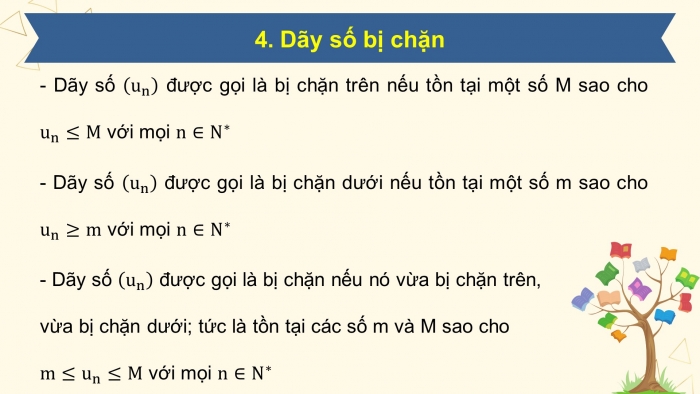
4. Dãy số bị chặn

- Dãy số  được gọi là bị chặn trên nếu tồn tại một số M sao cho  với mọi

- Dãy số  được gọi là bị chặn dưới nếu tồn tại một số m sao cho  với mọi

- Dãy số  - Dãy số  được gọi là bị chặn nếu nó vừa bị chặn trên,

vừa bị chặn dưới; tức là tồn tại các số m và M sao cho

 với mọi

LUYỆN TẬP, VẬN DỤNG

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Quy nạp toán học

Bài 1. Chứng minh rằng với mọi số nguyên dương n, ta có

Giải

Với , ta có:

Suy ra VT(1) = VP(1) với n = 1

Vậy (1) đúng với n = 1

Giả sử (1) đúng với n = k

Giải

Khí đó: . Ta phải chứng minh (1) đúng với n = k + 1 hay

Thật vậy

=

Vậy (1) đúng khi

Do đó theo nguyên lí quy nạp (1) đúng với mọi số nguyên dương n.

Bài 2. Chứng minh rằng với mọi số nguyên dương n ³ 2 , ta có

  (1)

Giải

Với n = 2, ta có VT(1)

Suy ra VT(1) = VP(1) với n = 2

Giả sử (1) đúng với n = k. Khi đó ta có