Giáo án chuyên đề Toán 12 kết nối tri thức 2024 (file word)
Tải giáo án chuyên đề Toán 12 kết nối tri thức 2024 (file word) mới nhất. Giáo án chuyên đề biên soạn chi tiết cẩn thận bám sát nội dung các chuyên đề bài học trong sách chuyên đề học tập chương trình lớp 12. Tài liệu biên soạn dưới dạng File word, font chữ Time New Roman, tải về chỉnh sửa được. Mời thầy cô tham khảo
Rõ nét về file powerpoint trình chiếu. => Xem thêm
Ngày soạn: .../.../...
Ngày dạy: .../.../...
CHUYÊN ĐỀ I: BIẾN NGẪU NHIÊN RỜI RẠC. CÁC SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN RỜI RẠC.
BÀI 1: BIẾN NGẪU NHIÊN RỜI RẠC VÀ CÁC SỐ ĐẶC TRƯNG.
- MỤC TIÊU:
- Kiến thức, kĩ năng:Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết khái niệm biến ngẫu nhiên rời rạc.
- Biết lập bảng phân phối xác suất của biến ngẫu nhiên rời rạc.
- Biết tính kì vọng, phương sai và độ lệch tiêu chuẩn của biến ngẫu nhiên rời rạc và giải thích ý nghĩa của chúng.
- Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá.
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm.
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Rèn luyện năng lực tư duy và lập luận toán học, năng lực mô hình hóa toán học và năng lực giải quyết vấn đề toán học thông qua việc mô hình hóa những vấn đề thực tế liên quan đến biến ngẫu nhiên rời rạc.
- Rèn luyện năng lực giao tiếp toán học.
- Phẩm chất
- Cóý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm, tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
- THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
- Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
- Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
- HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
- a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
- b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
- c) Sản phẩm: HS đưa ra được nhận định ban đầu về câu hỏi mở đầu.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV chiếu Slide dẫn dắt và yêu cầu HS thảo luận và nêu dự đoán về câu hỏi mở đầu.
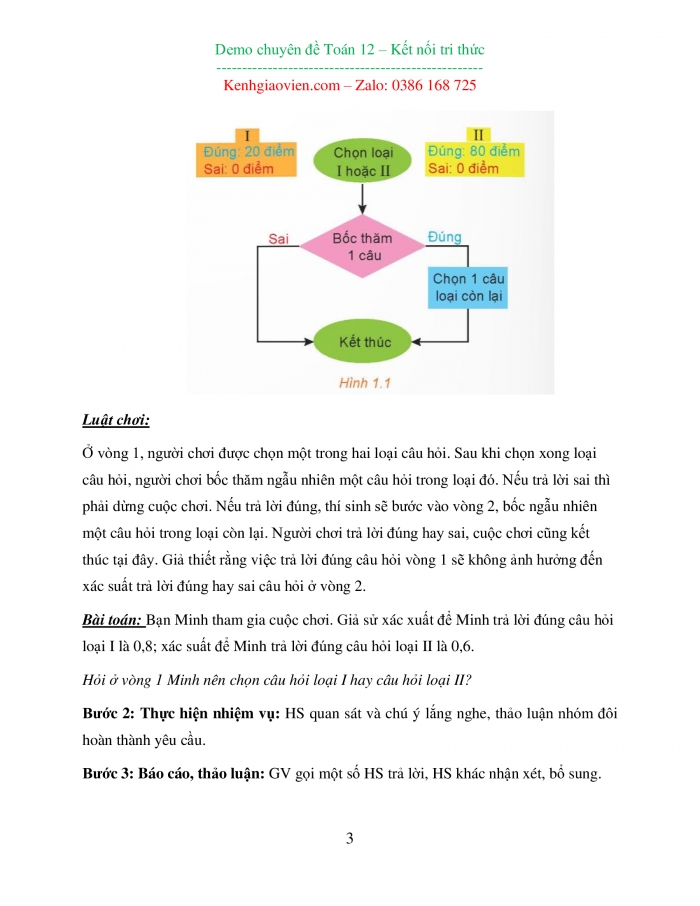
Trong một trò chơi, các câu hỏi gồm hai loại I và II:
- Với câu hỏi loại I: Trả lời đúng được 20 điểm. Trả lời sai không được điểm (0 điểm).
- Với câu hỏi loại II: Trả lời đúng được 80 điểm. Trả lời sai không được điểm (0 điểm).
Luật chơi:
Ở vòng 1, người chơi được chọn một trong hai loại câu hỏi. Sau khi chọn xong loại câu hỏi, người chơi bốc thăm ngẫu nhiên một câu hỏi trong loại đó. Nếu trả lời sai thì phải dừng cuộc chơi. Nếu trả lời đúng, thí sinh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi trong loại còn lại. Người chơi trả lời đúng hay sai, cuộc chơi cũng kết thúc tại đây. Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2.
Bài toán: Bạn Minh tham gia cuộc chơi. Giả sử xác xuất để Minh trả lời đúng câu hỏi loại I là 0,8; xác suất để Minh trả lời đúng câu hỏi loại II là 0,6.
Hỏi ở vòng 1 Minh nên chọn câu hỏi loại I hay câu hỏi loại II?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới: “Trong bài học này, chúng ta sẽ tìm hiểu một số nội dung cơ bản về biến ngẫu nhiên rời rạc.”.
Bài mới: Bài 1: Biến ngẫu nhiên rời rạc. Các số đặc trưng của biến ngẫu nhiên rời rạc.
- HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Biến ngẫu nhiên rời rạc và bảng phân bố xác suất của nó.
- a) Mục tiêu:
- Nhận biết khái niệm biến ngẫu nhiên rời rạc và bảng phân bố xác suất.
- b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện các hoạt động HĐ 1, 2; đọc hiểu Ví dụ 1, 2, 3,4; Luyện tập 1 và Vận dụng 1.
- c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi. HS nhận biết được khái niệm biến ngẫu nhiên rời rạc và bảng phân bố xác suất.
- d) Tổ chức thực hiện:
|
HĐ CỦA GV VÀ HS |
SẢN PHẨM DỰ KIẾN |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bước 1: Chuyển giao nhiệm vụ: Nhiệm vụ 1: Hình thành khái niệm biến ngẫu nhiên rời rạc. - GV cho HS thực hiện HĐ 1. Gieo một xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi X là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó. a) Các giá có thể có của X là? b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được X sẽ nhận giá trị nào không? - GV khái quát cho HS: Khi gieo xúc xắc cân đối đồng chất, có thể xuất hiện mặt 1 chấm, 2 chấm,…, 6 chấm. GV giới thiệu cho HS về khái niệm biến ngẫu nhiên rời rạc. GV yêu cầu HS khái quát định nghĩa biến ngẫu nhiên rời rạc.
- HS đọc Ví dụ 1. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 6 – 7 ) và trả lời câu hỏi sau: Nhắc lại khái niệm không gian mẫu và xác suất của một phép thử. Gợi ý trả lời: Cho T là một phép thử. - Tập hợp tất cả các kết quả có thể xảy ra của phép thử T được gọi là không gian mẫu của phép thử đó. Kí hiệu: Ω - Giả sử A là một biến cố được mô tả bằng . Xác xuất của biến cố A, kí hiệu P(A) được cho bởi công thức: P(A)= - GV gọi 1 HS bất kì đứng tại chỗ trả lời và giải thích. GV giới thiệu cho HS về bảng phân bố xác suất.
Nhiệm vụ 2: Củng cố khái niệm bảng phân bố xác suất của biến cố ngẫu nhiên rời rạc. - HS thực hiện HĐ 2. Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc X trong Ví dụ 1.
- GV gọi 1 HS lên bảng trình bày. - GV nêu câu hỏi mở: Em có nhận xét gì tổng xác suất của biến ngẫu nhiên X ở bảng trên? GV nêu tính chất bảng phân bố xác suất của biến ngẫu nhiên rời rạc.
- HS đọc Ví dụ 2. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 7 ).
- HS đọc Ví dụ 3. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 8) và trả lời câu hỏi sau: 1. Thế nào là hai biến cố xung khắc? 2. Hãy nhắc lại quy tắc cộng xác suất? Gợi ý trả lời: 1. Cho hai biến cố A và B cùng liên quan đến một phép thử T. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra. 2. Nếu hai biến cố A và B xung khắc thì xác suất để A hoặc B xảy ra là: . Cho biến cố đôi một xung khắc, xác suất để ít nhất một trong các biến cố xảy ra là: . - GV gọi 1 HS bất kì đứng tại chỗ trả lời và giải thích. - HS đọc Ví dụ 4. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 8 - 9) và trả lời câu hỏi sau: 1. Thế nào là hai biến cố giao nhau? 2. Hãy nhắc lại quy tắc nhân xác suất. Gợi ý trả lời: 1. Cho hai biến cố A và B cùng liên quan đến một phép thứ T. Biến cố “Cả A và B cùng xảy ra” được gọi là giao của hai biến cố A và B, kí hiệu là AB
2. Nếu hai biến cố A và B độc lập với nhau thì xác suất để A và B xảy ra là: P(AB) = P(A) . P(B) - GV gọi 1 HS bất kì đứng tại chỗ trả lời và giải thích. - HS thực hiện Luyện tập 1 - GV khái quát cho HS: Dựa vào Ví dụ 4 để hoàn thành Luyện tập 1.
- HS đọc Vận dụng 1. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 9). - GV đưa ra chú ý: a) Dựa vào Ví dụ 1 và Luyện tập 1 để tìm xác suất và lập bảng phân bố xác suất của X. b) Số lớn hơn 18 là 19 và 20. Tìm xác suất biến cố hợp của hai biến cố {X = 19} và {X = 20}. Bước 2: Thực hiện nhiệm vụ: - HS theo dõi SGK, chú ý nghe, tiếp nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ. Bước 3: Báo cáo, thảo luận: - HS giơ tay phát biểu, lên bảng trình bày - Một số HS khác nhận xét, bổ sung cho bạn. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm và yêu cầu HS ghi chép đầy đủ vào vở.
|
I. Biến ngẫu nhiên rời rạc và bảng phân bố xác suất của nó. 1. Biến ngẫu nhiên rời rạc. HĐ 1: a) Khi gieo một xúc xắc cân đối, đồng chất liên tiếp 6 lần thì số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo đó là: 0, 1, 2, 3, 4, 5, 6. b) Trước khi thực hiện việc gieo xúc xắc đó, ta không khẳng định được X sẽ nhận giá trị nào.
Khái niệm Đại lượng X được gọi là một biến ngẫu nhiên rời rạc nếu nó nhận một số hữu hạn các giá trị có thể. Các giá trị đó là các số và không dự đoán được trước khi phép thử được thực hiện.
Ví dụ 1 (SGK – tr.6) Tung một đồng xu cân đối, đồng chất liên tiếp 3 lần. Gọi X là số lần đồng xu xuất hiện mặt ngửa. a) X có là một biến ngẫu nhiên rời rạc không? b) Liệt kê các giá trị có thể của X và tính các xác suất để X nhận các giá trị đó? Hướng dẫn giải (SGK – tr.6 - 7)
Giả sử là một biến ngẫu nhiên rời rạc nhận giá trị với các xác suất tương ứng là tức là Bảng sau đây được gọi là bảng phân bố xác suất của biến ngẫu nhiên rời rạc X.
2. Bảng phân bố xác suất của biến cố ngẫu nhiên rời rạc. HĐ2:
Trong bảng phân bố xác suất của biến ngẫu nhiên rời rạc X, ta có: . Ví dụ 2 (SGK – tr.7) Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
Tìm a. Hướng dẫn giải (SGK – tr 7). Ví dụ 3 (SGK – tr.7) Giả sử số vụ vi phạm Luật giao thông trên một đoạn đường vào tối thứ Bảy là một biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
Tính xác suất để tối thứ Bảy: a) Xảy ra nhiều nhất 1 vụ vi phậm Luật giao thông; b) Xảy ra ít nhất 3 vụ vi phậm Luật giao thông; c) Xảy ra ít nhất 2 vụ vi phạm Luật giao thông. Hướng dẫn giải (SGK – tr 8).
Ví dụ 4 (SGK – tr.8) Một túi đựng 6 viên bi đỏ và 4 viên bi xanh. Các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên đồng thời 3 viên bị từ trong túi. Gọi X là số viên bi xanh trong 3 viên bi lấy ra. Lập bảng phân bố xác suất của X. Hướng dẫn giải (SGK – tr 8 - 9).
Luyện tập 1 (SGK tr. 9) Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X. Giải Các giá trị có thể của X thuộc tập {0, 1, 2, 3}. Số cách chọn 3 học sinh trong 16 học sinh là: cách. Ta có: - Biến cố {X = 0} là: “Lấy được 3 học sinh đều là nữ” Số kết quả thuận lợi cho biến cố {X = 0} là . . - Biến cố {X = 1} là: “Lấy được 1 học sinh nam và 2 học sinh nữ” Có cách chọn 1 học sinh nam trong 10 học sinh nam và cách chọn 2 học sinh nữ trong 6 học sinh nữ. Theo quy tắc nhân ta có: cách chọn 1 học sinh nam và 2 học sinh nữ. Số kết quả thuận lợi cho biến cố {X = 1} là . . - Biến cố {X = 2} là: “Lấy được 2 học sinh nam và 1 học sinh nữ” Có cách chọn 2 học sinh nam trong 10 học sinh nam và cách chọn 1 học sinh nữ trong 6 học sinh nữ. Theo quy tắc nhân ta có: cách chọn 2 học sinh nam và 1 học sinh nữ. Số kết quả thuận lợi cho biến cố {X = 2} là . . - Biến cố {X = 3} là: “Lấy được 3 học sinh đều là nam” Số kết quả thuận lợi cho biến cố {X = 3} là . . Bảng phân bố xác suất của X là:
Vận dụng 1 (SGK tr. 9) Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trông hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra. a) Lập bảng phân bố xác suất của X. b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi. Hướng dẫn giải (SGK – tr. 9). Giải a) Tập các giá trị có thể có của X là: {3; 4;…; 20} Ta tính , với Số kết quả có thể là Biến cố là biến cố: “Trong 3 quả cầu lấy ra có một quả cầu đánh số và 2 quả cầu đánh số nhỏ hơn ” Số kết quả thuận lợi là . Vậy
Với , ta có:
Với , ta có:
…. Với , ta có:
Với , ta có:
Bảng phân bố xác suất của X là:
b) Biến cố “Người chơi thắng” là biến cố hợp của hai biến cố và .
|
Hoạt động 2: Các số đặc trưng của biến ngẫu nhiên rời rạc.
- a) Mục tiêu:
- Nhận biết được khái niệm kì vọng, phương sai và độ lệch chuẩn.
- b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý nghe giảng, thực hiện các hoạt động HĐ 3, 4; Ví dụ5, 6, 7; Luyện tập 2, 3 và Vận dụng 2.
- c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi. HS nhận biết được khái niệm kì vọng, phương sai và độ lệch chuẩn.
- d) Tổ chức thực hiện:
|
HĐ CỦA GV VÀ HS |
SẢN PHẨM DỰ KIẾN |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bước 1: Chuyển giao nhiệm vụ: - GV cho HS thực hiện HĐ 3 theo nhóm đôi. Giả sử số vụ vi phạm Luật giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật giao thông trên đoạn đường AB trong 98 buổi tối thứ Bảy đó? - GV gợi mở: 1. Tính và lập bảng phân bố xác suất của X. 2. Tính trung bình số vụ vi phạm Luật giao thông trên đoạn đường AB trong 98 buổi tối thứ Bảy theo biểu thức sau:
- GV mời 2 đại diện nhóm nhanh nhất đứng tại chỗ trả lời, mỗi nhóm một phần.
- GV giới thiệu cho HS khái niệm kì vọng.
- GV nêu nhận xét
- HS đọc Ví dụ 5. - GV yêu cầu HS đọc hướng dẫn giải (SGK – tr. 11). - GV lưu ý cho HS: Để tính được trung bình số cá ông An câu được trong một buổi tối đi câu ta sử dụng công thức tính kì vọng - GV cho HS thực hiện Luyện tập 2 theo nhóm đôi. - GV lưu ý cho HS: Dựa vào Ví dụ 1 để trả lời câu hỏi. - GV gọi đại diện 1 nhóm trình bày đáp án.
- HS đọc Ví dụ 6. - GV cho HS đọc hướng dẫn giải (SGK – tr. 11) - GV nêu câu hỏi mở: 1. Thế nào là hai biến cố đối nhau? 2. Thế bào là hai biến cố độc lập? - Gợi ý trả lời 1. Cho biến cố A, khi đó biến cố “không A”, kí hiệu là gọi là biến cố đối của biến cố A. Ta nói A và là hai biến cố đối của nhau. 2. Hai biến cố được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia. Khi hai biến cố A và B độc lập với nhau thì A và , và B, và cũng là hai biến cố độc lập. - GV lưu ý cho HS: Sử dụng quy tắc cộng, quy tắc nhân xác suất để hoàn thành bài tập. - HS đọc Vận dụng 2. - GV cho HS đọc hướng dẫn giải (SGK – tr. 12)
- GV cho HS thực hiện HĐ 4 theo nhóm đôi. Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồ với xác suất tương ứng là và . Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau. a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2. b) Nhà đầu tư nên chọn phương án nào? - GV hướng dẫn HS: Đặt X là doanh thu đạt được với phương án 1, Y là doanh thu đạt được với phương án 2. 1. Tính và 2. Đặt = , = Tính giá trị của biểu thức:
3. Tính , So sánh và . - GV giới thiệu khái niệm phương sai và độ lệch chuẩn.
- GV nêu nhận xét
- HS đọc Ví dụ 7. - GV cho HS đọc hướng dẫn giải (SGK – tr. 12) - GV gọi 1 HS bất kì đứng dậy trả lời và giải thích.
- GV cho HS thực hiện Luyện tập 3. - GV hướng dẫn HS: Dựa vào Ví dụ 7 để hoàn thành bài tập. - GV mời HS có kết quả nhanh nhất lên bảng trình bày. Bước 2: Thực hiện nhiệm vụ: - HĐ cá nhân: HS suy nghĩ, quan sát thực hiện thao tác theo hướng dẫn. Cả lớp chú ý thực hiện các yêu cầu của GV. - GV: quan sát và trợ giúp HS. Bước 3: Báo cáo, thảo luận: - HS trả lời trình bày miệng/ trình bày bảng, cả lớp nhận xét, GV đánh giá, dẫn dắt, chốt lại kiến thức. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm. |
II. Các số đặc trưng của biến ngẫu nhiên rời rạc. a) Kì vọng HĐ 3: Ta có: ; ; ; ; ; . Bảng phân bố xác xuất là:
Trung bình số vụ vi phạm Luật giao thông trên đoạn đường AB trong 98 buổi tối thứ Bảy là: (vụ). Khái niệm Cho X là một biến ngẫu nhiên rời rạc với bảng phân bố xác suất:
Kì vọng của X, kí hiệu E(X), là một số được tính theo công thức sau:
Nhận xét * Kì vọng E(X) là một số cho ta một ý niệm về độ lớn trung bình của X nên kì vọng E(X) còn được gọi là giá trị trung bình của X. * E(X) được tính thông qua bảng phân bố xác suất của X. * E(X) không nhất thiết thuộc tập các giá trị có thể của X. Ví dụ 5 (SGK – tr. 11) Trong mỗi buổi tối ông An đi câu cá, ông có thể câu được 0; 1; 2; 3; 4 con cá với xác suất tương ứng là 0,16; 0, 17; 0, 25; 0, 28 và 0, 13. Hỏi trung bình ông An câu được bao nhiêu cá trong một buổi đi câu? Hướng dẫn giải (SGK – tr. 11). Luyện tập 2 (SGK – tr. 11) Giả sử số vụ vi phạm Luật giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với xác xuất tương ứng là 0,1; 0,2; 0,25; 0,25 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật giao thông trên đoạn đường đó vào tối thứ Bảy? Giải Gọi X là số vụ vi phạm Luật giao thông trên đoạn đường đó vào tối thứ Bảy. Theo giả thiết X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất như sau:
Ta có:
Vậy trung bình đoạn đường xảy ra 2,3 số vụ vi phạm Luật giao thông trong buổi tối thứ Bảy. Ví dụ 6 (SGK – tr. 11) Trở lại tình huống mở đầu. Giả sử ở vòng 1 bạn Minh bốc ngẫu nhiên một câu hỏi loại I. Hỏi trung bình Minh nhận được bao nhiêu điểm? Hướng dẫn giải (SGK – tr. 11 - 12).
Vận dụng 2 (SGK – tr. 12) Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II. a) Hỏi trung bình Minh nhận được bao nhiêu điểm? b) Ở vòng 1 Minh nên chọn câu hỏi nào? Hướng dẫn giải (SGK – tr. 12). b) Phương sai và độ lệch chuẩn. HĐ 4: a) Ta có:
Vậy, b) Ta có:
Ta thấy, nghĩa là doanh thu theo phương án 1 ổn định hơn doanh thu theo phương án 2. Vậy nhà đầu tư nên chọn phương án 1.
Định nghĩa Cho X là một biến ngẫu nhiên rời rạc với bảng phân bố xác suất như sau:
1) Phương sai của X, kí hiệu là , là một số được tính theo công thức sau:
Trong đó 2) Độ lệch chuẩn của X, kí hiệu là , là căn bậc hai số học của phương sai:
Nhận xét * còn có thể tính theo công thức sau:
Công thức trên giúp ta tính nhanh hơn công thức vì bớt đi được phép trừ. * Phương sai là một số không âm. Nó cho ta một ý niệm về mức độ phân tán các giá trị của X xung quanh kì vọng . Phương sai càng lớn thì độ phân tán càng lớn. * Cũng như phương sai, độ lệch chuẩn cho ta một ý niệm về mức độ phân tán các giá trị của X xung quanh kì vọng . * Phương sai không có cùng đơn vị đo với X, còn độ lệch chuẩn có cùng đơn vị đo với X. Ví dụ 7 (SGK – tr. 12) Cho bảng ngẫu nhiên rời rạc X với phân bố xác suất:
a) Tính và theo định nghĩa. b) Tính theo công thức . Tham khảo hướng dẫn giải (SGK – tr. 12)
Luyện tập 3 (SGK – tr 12) Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
a) Tính và theo định nghĩa. b) Tính theo công thức . Giải a) Ta có:
Theo định nghĩa phương sai, ta có:
b) Theo công thức , ta có:
|
- HOẠT ĐỘNG LUYỆN TẬP
- a) Mục tiêu:Học sinh củng cố lại kiến thức đã học.
- b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1, 2 (SGK – tr. 13).
- c) Sản phẩm học tập: Câu trả lời của HS. HS nhận biết được khái niệm biến ngẫu nhiên, kì vọng, phương sai và độ lệch chuẩn.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS hoạt động thực hiện Bài 1, 2 (SGK – tr. 13).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác.
Kết quả:
Bài 1.
- a) Xác suất để xảy ra ít nhất một ca cấp cứu ở bệnh viện vào tối thứ Bảy là :
- b) Xác suất phải tăng cường bác sĩ trực tối thứ Bảy ở bệnh viện đó là :
- c) Ta có :
.
Bài 2.
- a) Xác suất để xảy ra ít nhất 2 cuộc gọi đến trung tâm cứu hộ là :
- b) Xác suất để xảy ra nhiều nhất 3 cuộc gọi đến trung tâm cứu hộ đó là :
- c) Ta có :
Câu hỏi trắc nghiệm
Câu 1. Cho X là biến ngẫu nhiên có bảng phân bố xác suất sau:
|
|
1 |
2 |
3 |
4 |
|
|
0,1 |
0,3 |
0,3 |
|
Chọn khẳng định đúng:
|
A. . |
B. . |
|
C. . |
D. . |
Câu 2.Tung một đồng xu cân đối, đồng chất 3 lần. Gọi X là số mặt sấp xuất hiện. Khi đó, khẳng định nào sau đây sai?
|
A. . |
|
B. . |
|
C. . |
|
D.. |
Câu 3. Biến ngẫu nhiên nhận các giá trị với các xác suất tương ứng thoả mãn:
|
A. . |
|
B. . |
|
C. . |
|
D. . |
Câu 4. Cho biến ngẫu nhiên có bảng phân bố xác suất dưới đây
|
|
1 |
2 |
3 |
4 |
|
|
0,5 |
|
0,1 |
0,1 |
Giá trị của là:
|
A. 0,4. |
B. 0,3. |
C. 0,2. |
D. 0,5. |
Câu 5. Chọn công thức đúng:
|
A. . |
|
B. . |
|
C. . |
|
D. . |
Câu 6. Cho bảng phân bố xác suất sau:
|
|
5 |
6 |
7 |
8 |
|
|
0,3 |
0,4 |
0,2 |
0,1 |
Khi đó, kỳ vọng của biến cố là:
|
A. 0,25. |
B. 6,5. |
C. 1,525. |
D. 6,1. |
Câu 7. Một hộp có 7 viên bi đỏ và 3 viên bị vàng. Chọn ngẫu nhiên 2 viên bi. Tính xác suất sao cho 2 viên bi được chọn đều là màu vàng.
|
A. . |
B. . |
C. . |
D. . |
Câu 8. Cho và là hai biến cố đối nhau. Chọn câu đúng?
|
A. . |
|
B. . |
|
C. . |
|
D. . |
Câu 9. Chủ vườn lan để nhầm 20 chậu lan có hoa màu đỏ với 100 chậu lan có hoa màu tím. Một hách hàng chọn ngẫu nhiên 15 chậu từ 120 chậu lan đó. Gọi là số chậu lan có hoa màu tím khách chọn được. Giá trị của và là:
|
A. . |
B. . |
|
C. . |
D. . |
Câu 10. Trong một đợt xổ số người ta phát hành 100 000 vé trong đó có 10 000 trúng thưởng. Hỏi 1 người muốn trúng ít nhất một vé với xác suất lớn hơn 95% thì cần phải mua tối đa bao nhiêu vé?
|
A. 2 vé. |
B. 12 vé. |
C. 27 vé. |
D. 29 vé. |
Đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
D |
B |
B |
B |
D |
A |
C |
C |
D |
- HOẠT ĐỘNG VẬN DỤNG
- a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
- b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập 3, 4,5 (SGK – tr. 13).
- c) Sản phẩm: Kết quả thực hiện các bài tập. HS vận dụng các khái niệm của biến ngẫu nhiên, kì vọng, phương sai và độ lệch chuẩn để giải quyết các bài toán.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 3, 4, 5 (SGK – tr. 13).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: Đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải.
Gợi ý đáp án:
Bài 3.
- a) Các giá trị có thể của X thuộc tập :
Số cách chọn 3 tấm thẻ trong 16 tấm thẻ là: cách.
Ta có:
- Biến cố {X = 0} là: “Lấy được 3 tấm thẻ màu xanh”
Số kết quả thuận lợi cho biến cố {X = 0} là .
.
- Biến cố {X = 1} là: “Lấy được 1 tấm thẻ màu đỏ và 2 tấm thẻ màu xanh”
Có cách chọn 1 tấm thẻ màu đỏ trong 10 tấm thẻ màu đỏ và cách chọn 2 tấm thẻ màu xanh trong 6 tấm thẻ màu xanh.
Theo quy tắc nhân ta có: cách chọn 1 tấm thẻ màu đỏ và 2 tấm thẻ màu xanh.
Số kết quả thuận lợi cho biến cố {X = 1} là .
.
- Biến cố {X = 2} là: “Lấy được 2 tấm thẻ màu đỏ và 1 tấm thẻ màu xanh”
Có cách chọn 2 tấm thẻ màu đỏ trong 10 tấm thẻ màu đỏ và cách chọn 1 tấm thẻ màu xanh trong 6 tấm thẻ màu xanh.
Theo quy tắc nhân ta có: cách chọn 2 tấm thẻ màu đỏ và 1tấm thẻ màu xanh.
Số kết quả thuận lợi cho biến cố {X = 2} là .
.
- Biến cố {X = 3} là: “Lấy được 3 tấm thẻ màu đỏ”
Số kết quả thuận lợi cho biến cố {X = 3} là .
.
Bảng phân bố xác suất của X là:
|
X |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
- b) Ta có:
- Biến cố {X = 0} là: “Lấy được 3 tấm thẻ màu xanh”
(điểm)
- Biến cố {X = 1} là: “Lấy được 1 tấm thẻ màu đỏ và 2 tấm thẻ màu xanh”
(điểm)
- Biến cố {X = 2} là: “Lấy được 2 tấm thẻ màu đỏ và 1 tấm thẻ màu xanh”
(điểm)
- Biến cố {X = 3} là: “Lấy được 3 tấm thẻ màu đỏ”
(điểm)
Bảng phân bố xác suất của Y là :
|
Y |
24 |
21 |
18 |
15 |
|
P |
|
|
|
|
Bài 4.
Gọi là “Số phát bắn trượt bia của An” và là “Số phát bắn trượt bia của Bình”
Các giá trị có thể của X thuộc tập :
Xác suất để An bắn trúng 1 phát là :
Xác suất để An bắn trúng 2 phát là :
Xuất để An bắn trượt 2 phát là :
Bảng phân bố của X là :
|
X |
0 |
1 |
2 |
|
P |
0,36 |
0,48 |
0,16 |
Các giá trị có thể của Y thuộc tập :
Xác suất để An bắn trúng 1 phát là :
Xác suất để An bắn trúng 2 phát là :
Xuất để An bắn trượt 2 phát là :
Bảng phân bố của Y là :
|
X |
0 |
1 |
2 |
|
P |
0,25 |
0,5 |
0,25 |
- b)
Bài 5.
Gọi X là kết quả thu được.
Các giá trị có thể của X thuộc:
Số kết quả có thể là:
- Biến cố {X = 2} là: “Lấy được 2 quả cầu ghi số 1”
Số kết quả thuận lợi cho biến cố {X = 2} là .
.
- Biến cố {X = 3} là: “Lấy được 1 quả cầu ghi số 1 và 1 quả cầu ghi số 2”
Số kết quả thuận lợi cho biến cố {X = 3} là .
.
- Biến cố {X = 4} là: “Lấy được 1 quả cầu ghi số 1 và 1 quả cầu ghi số 3” và “Lấy được 2 quả cầu ghi số 2 ”
Số kết quả thuận lợi cho biến cố {X = 4} là .
.
- Biến cố {X = 5} là: “Lấy được 1 quả cầu ghi số 1 và 1 quả cầu ghi số 4” và “Lấy được 1 quả cầu ghi số 2 và 1 quả cầu ghi số 3”
Số kết quả thuận lợi cho biến cố {X = 5} là .
.
- Biến cố {X = 6} là: “Lấy được 1 quả cầu ghi số 2 và 1 quả cầu ghi số 4” và “Lấy được 2 quả cầu ghi số 3”
Số kết quả thuận lợi cho biến cố {X = 6} là .
.
- Biến cố {X = 7} là: “Lấy được 1 quả cầu ghi số 3 và 1 quả cầu ghi số 4”
Số kết quả thuận lợi cho biến cố {X = 7} là .
.
Bảng phân bố xác suất của X là :
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
|
P |
|
|
|
|
|
|
* HƯỚNG DẪN VỀ NHÀ
- Ghi nhớ kiến thức trong bài.
- Hoàn thành các bài tập trong SBT
- Chuẩn bị bài mới: “Biến ngẫu nhiên có phân bố nhị thức và áp dụng”.
Hình ảnh về file sile, ppt trình chiếu
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Giáo án chuyên đề Toán 12 kết nối tri thức, soạn giáo án sách chuyên đề Toán 12 kết nối tri thức,, giáo án chuyên đề học tập lớp 12 sách mới chương trình 2023-2024
