Tải giáo án Powerpoint Toán hình học 12 chân trời sáng tạo 2024 mới nhất

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC MÔN TOÁN! 

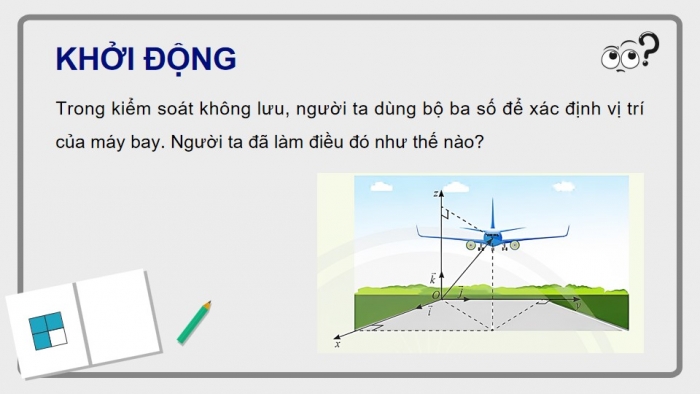
KHỞI ĐỘNG 

Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó như thế nào? 

CHƯƠNG II. VECTƠ VÀ HỆ TỌA ĐỘ TRONG KHÔNG GIAN 

BÀI 2. TỌA ĐỘ CỦA VECTƠ TRONG KHÔNG GIAN 

NỘI DUNG BÀI HỌC 

01 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN 

HĐKP1: Cho hình lập phương OABC.O′A′B′C′ có cạnh bằng 1. Đặt i ⃗=(OA) ⃗; j ⃗=(OC) ⃗;k ⃗=(OO′) ⃗. 

1. a) Nêu nhận xét về phương và độ dài của ba vectơ i ⃗,j ⃗,k ⃗.
2. b) Nêu nhận xét về ba trục toạ độ (O;i ⃗),(O;j ⃗),(O;k ⃗).

Trả lời: 

1. a) Ba vectơ i ⃗;j ⃗;k ⃗ có phương đôi một vuông góc với nhau và độ dài ba vectơ đều bằng 1.
2. b) Ba trục tọa độ (O;i ⃗),(O;j ⃗),(O;k ⃗)  đôi một vuông góc với nhau.

Hệ tọa độ trong không gian 

Trong không gian, cho ba trục Ox, Oy, Oz đôi một vuông góc. Gọi i ⃗;j ⃗;k ⃗ lần lượt là ba vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz trong không gian hay gọi đơn giản là hệ tọa độ Oxyz. 

Nhận xét: 

1. a) Điểm O được gọi là gốc tọa độ.

Các trục Ox, Oy, Oz được gọi là các trục tọa độ. 

Các mặt phẳng (Oxy),(Oyz),(Ozx) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ. 

Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz. 

1. b) Vì i ⃗;j ⃗;k ⃗ là ba vectơ đơn vị đôi một vuông góc với nhau nên ta có:

i ⃗^2=j ⃗^2=k ⃗^2=1 và i ⃗.j ⃗=j ⃗.k ⃗=k ⃗.i ⃗=0. 

Ví dụ 1:  Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và có độ dài bằng 1. Vẽ hệ trục tọa độ Oxyz có gốc là O, các điểm A,B,C lần lượt nằm trên các tia Ox,Oy,Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ. 

Giải: 

Với O là gốc toạ độ, ta vẽ được các trục Ox,Oy,Oz như Hình 3.  

Ba vecto đơn vị trên ba trục lần lượt là i ⃗=(OA) ⃗;       j ⃗=(OB) ⃗;k ⃗=(OC) ⃗. 

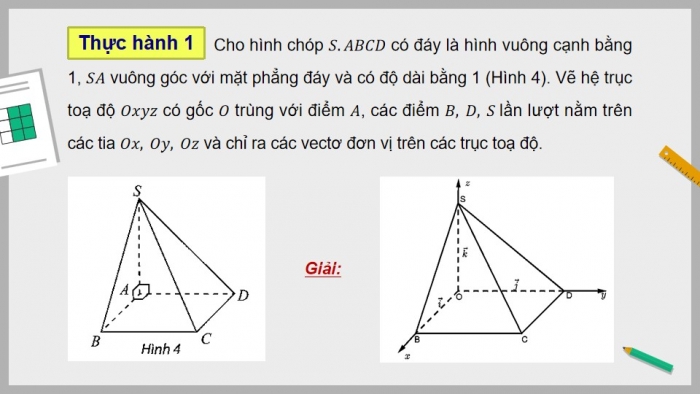
Thực hành 1:  Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ. 

Giải: 

Vận dụng 1 

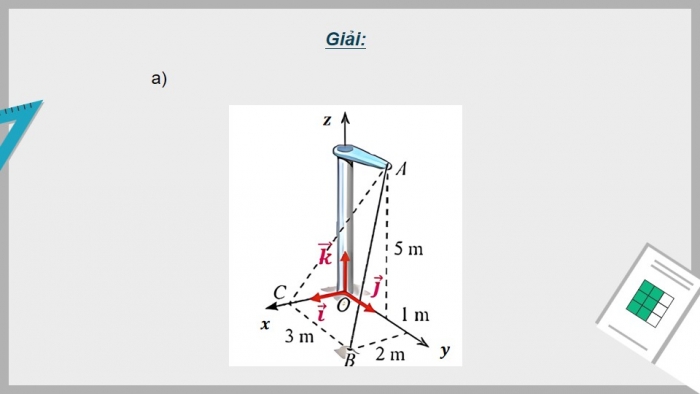
Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b. 

1. a) Hãy vẽ ba vectơ đơn vị i ⃗;j ⃗;k ⃗ lần lượt trên ba trục tọa độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1m).
2. b) Biểu diễn các vectơ (OC) ⃗, (OB) ⃗, (OA) ⃗, (AB) ⃗ theo i ⃗;j ⃗;k ⃗.

Giải: 

1. a)
2. b) Ta có: C∈Ox và OC=2

Vậy (OC) ⃗=2i ⃗ 

Áp dụng quy tắc hình bình hành, ta có: 

(OB) ⃗=(OC) ⃗+(OD) ⃗=2i ⃗+3j ⃗ 

Áp dụng quy tắc hình bình hành, ta có: 

(OA) ⃗=2j ⃗+5k ⃗ 

Ta có:  

(AB) ⃗=(OB) ⃗−(OA) ⃗=2i ⃗+3j ⃗−2j ⃗−5k ⃗ 

                             =2i ⃗+j ⃗−5k ⃗ 

02 TOẠ ĐỘ CỦA ĐIỂM VÀ VECTO 

Tọa độ của điểm 

HĐKP2: Cho hình hộp chữ nhật OABC.O′A′B′C′ có cạnh OA=3,      OC=5, OO^′=2. Vẽ ba vectơ đơn vị i ⃗;j ⃗;k ⃗ lần lượt trên các cạnh OA, OC, OO′. Biểu diễn (OB′) ⃗ theo ba vectơ i ⃗;j ⃗;k ⃗. 

Trả lời: 

Ta có: 

(OB′) ⃗=(OO′) ⃗+(OA) ⃗+(OC) ⃗=3i ⃗+5j ⃗+2k ⃗ 

Định nghĩa 

Trong không gian Oxyz, cho điểm M. Nếu (OM) ⃗=xi ⃗+yj ⃗+zk ⃗ thì ta gọi bộ ba số (x,y,z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz và viết M=(x;y;z) hoặc M(x;y;z); x là hoành độ, y là tung độ, z là cao độ của điểm M. 

Ví dụ 2:  Cho hình hộp chữ nhật OABC.O′A′B′C′ có cạnh OA=4, OC=6, OO^′=3. Chọn hệ trục tọa độ Oxyz có gốc tọa độ O; các điểm A, C, O′ lần lượt nằm trên các tia Ox, Oy, Oz. Xác định tọa độ các điểm A, B, B′. 

Giải: 

Ta có:  

(OA) ⃗=4i ⃗+0j ⃗+0k ⃗, suy ra A(4;0;0); 

(OB) ⃗=(OA) ⃗+(OC) ⃗=4i ⃗+6j ⃗+0k ⃗,      suy ra B(4;6;0); 

(OB′) ⃗=(OA) ⃗+(OC) ⃗+(OO′) ⃗=4i ⃗+6j ⃗+3k ⃗, suy ra B′(4;6;3). 

Thực hành 2:  Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 5. Chọn hệ trục tọa độ Oxyz có gốc tọa độ O trùng với A; các điểm B, D, A′ lần lượt nằm trên các tia Ox, Oy, Oz. Xác định tọa độ các điểm B, C, C′. 

Giải: 

Ta có: 

(OB) ⃗=5i ⃗+0j ⃗+0k ⃗, suy ra B(5;0;0) 

(OC) ⃗=(OB) ⃗+(OD) ⃗=5i ⃗+5j ⃗+0k ⃗, suy ra C(5;5;0) 

(OC′) ⃗=(OC) ⃗+(OO′) ⃗=5i ⃗+5j ⃗+5k ⃗, suy ra C′(5;5;5) 

Tọa độ của vectơ 

HĐKP3: Trong không gian Oxyz, cho vectơ a ⃗. Vẽ điểm A sao cho (OA) ⃗=a ⃗ Gọi (a_1;a_2;a_3) là tọa độ của điểm A. Hãy biểu diễn a ⃗ theo ba vectơ      đơn vị i ⃗;j ⃗;k ⃗. 

Trả lời: 

Ta có: (OA) ⃗=a_1i ⃗+a_2j ⃗+a_3k ⃗ 

Mà (OA) ⃗=a ⃗ 

Suy ra a ⃗=a_1i ⃗+a_2j ⃗+a_3k ⃗. 

Định nghĩa 

Trong không gian Oxyz, cho vectơ a ⃗. Nếu a ⃗=a_1i ⃗+a_2j ⃗+a_3k ⃗ thì ta gọi bộ ba số (a_1;a_2;a_3) là tọa độ của vectơ a ⃗ đối với hệ tọa độ Oxyz và viết           a ⃗=(a_1;a_2;a_3) hoặc a ⃗(a_1;a_2;a_3).   

Nhận xét: Trong không gian Oxyz, ta có: 

Tọa độ của điểm M là tọa độ của vectơ (OM) ⃗, tức là  

M=(x;y;z)⇔(OM) ⃗=(x;y;z). 

Điều kiện để hai vectơ bằng nhau: 

Cho a ⃗=(x;y;z),b ⃗=(x′;y′;z′). Khi đó: a ⃗=b ⃗⇔{█(x=x′@y=y′@z=z′.)┤ 

Ví dụ 3: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A′B′C′D′ có đỉnh A trùng với gốc O, các vectơ (AB) ⃗,(AD) ⃗,(AA′) ⃗ theo thứ tự cùng hướng với i ⃗;j ⃗;k ⃗ và có AB=8, AD=6, AA^′=4. Tìm tọa độ các vectơ (AB) ⃗,(AC) ⃗,(AC′) ⃗ và (AM) ⃗ với M là trung điểm của cạnh C′D′. 

Giải: 

Để tìm toạ độ của vectơ (AB) ⃗, ta cần biểu diễn (AB) ⃗ theo ba vectơ i ⃗;j ⃗;k ⃗. 

Do (AB) ⃗ cùng hướng với i ⃗ và |(AB) ⃗|=AB=8=8 |i ⃗| 

nên (AB) ⃗=8i ⃗ hay (AB) ⃗=8i ⃗+0j ⃗+0k ⃗ 

Tương tự, ta có: (AD) ⃗=0i ⃗+6j ⃗+0k ⃗,  (AA′) ⃗=0i ⃗+0j ⃗+4k ⃗ 

Trong hình bình hành ABCD, ta có:  

(AC) ⃗=(AB) ⃗+(AD) ⃗=8i ⃗+6j ⃗+0k ⃗ 

Trong hình bình hành AA′C′C, ta có: 

(AC′) ⃗=(AC) ⃗+(AA′) ⃗=8i ⃗+6j ⃗+4k ⃗ 

Suy ra (AB) ⃗ =(8; 0; 0); (AC) ⃗=(8; 6; 0); (AC′) ⃗=(8; 6; 4) 

Vì (AM) ⃗= 1/2((AC′) ⃗+(AD′) ⃗)=1/2((AC′) ⃗+(AD) ⃗+(AA′) ⃗) 

1/2(8i ⃗+6j ⃗+4k ⃗+6j ⃗+4k ⃗)=4i ⃗+6j ⃗+4k ⃗  

Nên (AM) ⃗=(4;6;4). 

Thực hành 3:  Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3. 

1. a) Vẽ hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ.
2. b) Trong hệ tọa độ nói trên, tìm tọa độ các vectơ (AB) ⃗,(AD) ⃗,(AS) ⃗ và (AM) ⃗ với M là trung điểm của cạnh SC.

Giải: 

1. a)
2. b) Ta có:

(AB) ⃗=2i ⃗+0j ⃗+0k ⃗, suy ra (AB) ⃗(2;0;0). 

(AD) ⃗=0i ⃗+2j ⃗+0k ⃗, suy ra (AD) ⃗(0;2;0). 

(AS) ⃗=0i ⃗+0j ⃗+3k ⃗, suy ra (AS) ⃗(0;0;3). 

Vì M là trung điểm SC 

⇒(AM) ⃗=1/2((AS) ⃗+(AC) ⃗)=1/2((AS) ⃗+(AB) ⃗+(AD) ⃗)=1/2(2i ⃗+2j ⃗+3k ⃗)=i ⃗+j ⃗+3/2k ⃗ 

Vậy (AM) ⃗=(1;1;3/2). 

Vận dụng 2 

Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM=14, (NOB) ̂=32°, (MOC) ̂=65°. 

Tìm tọa độ điểm M. 

Giải: 

Xét ∆OMC có: 

OC=OM.cos65°≈5,92;CM=OM.sin65≈12,69 

Xét ∆ONB có: 

NB=ON.tan32°≈7,93;OB=ON:cos32°≈14,96 

Áp dụng quy tắc hình bình hành, ta có: 

    (OM) ⃗=(OA) ⃗+(OB) ⃗+(OC) ⃗≈7,93i ⃗+14,96j ⃗+5,92k ⃗ 

       Suy ra, M≈(7,93;14,96;5,92) 

LUYỆN TẬP 

...