Tải giáo án Powerpoint Toán đại số 12 chân trời sáng tạo 2024 mới nhất

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN! 

KHỞI ĐỘNG 

Trong 8 phút đầu kể từ khi xuất phát, độ cao ℎ (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức ℎ(t)=6t^3−81t^2+324t. Đồ thị của hàm số ℎ(t) được biểu diễn trong hình bên. 

Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? 

Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt? 

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 

BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ 

NỘI DUNG BÀI HỌC 

01 TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 

Nhắc lại về tính đồng biến, nghịch biến của hàm số 

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f(x) xác định trên K. 

Hàm số y=f(x) gọi là đồng biến (tăng) trên K nếu với mọi x_1,x_2 thuộc K mà x_1<x_2 thì f(x_1)<f(x_2). 

Hàm số y=f(x) gọi là nghịch biến (giảm) trên K nếu với mọi x_1,x_2 thuộc K mà x_1<x_2 thì f(x_1)>f(x_2). 

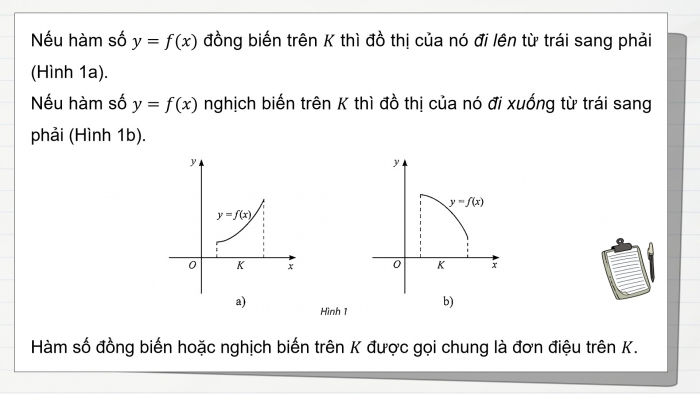
Nếu hàm số y=f(x) đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải (Hình 1a). 

Nếu hàm số y=f(x) nghịch biến trên K thì đồ thị của nó đi xuống từ trái sang phải (Hình 1b). 

Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K. 

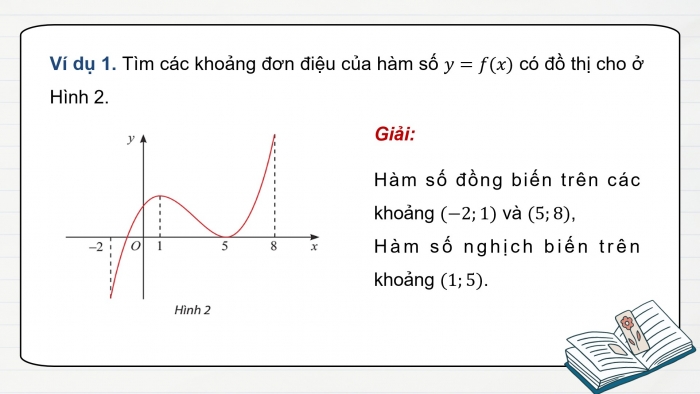
Ví dụ 1. Tìm các khoảng đơn điệu của hàm số y=f(x) có đồ thị cho ở Hình 2. 

Giải: 

Hàm số đồng biến trên các khoảng (−2;1) và (5;8),  

Hàm số nghịch biến trên khoảng (1;5). 

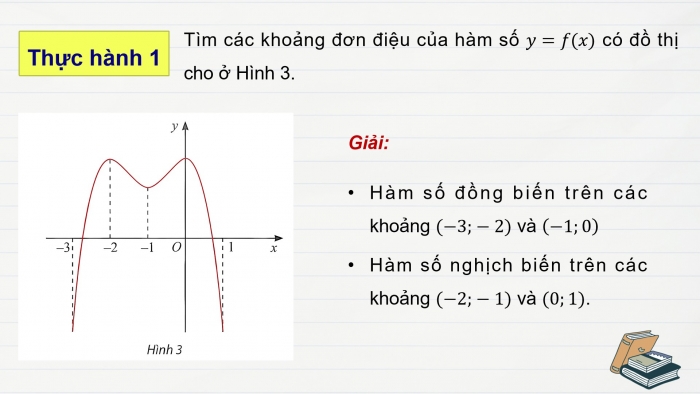
Thực hành 1 

Tìm các khoảng đơn điệu của hàm số y=f(x) có đồ thị cho ở Hình 3. 

Giải: 

Hàm số đồng biến trên các khoảng (−3;−2) và (−1;0) 

Hàm số nghịch biến trên các khoảng (−2;−1) và (0;1). 

Tính đơn điệu của hàm số 

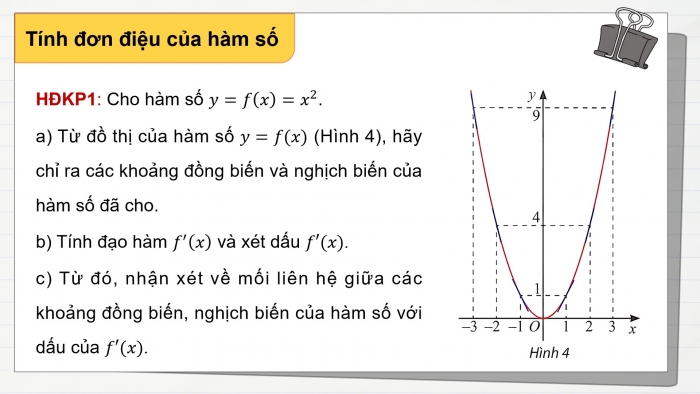
HĐKP1: Cho hàm số y=f(x)=x^2. 

1. a) Từ đồ thị của hàm số y=f(x) (Hình 4), hãy chỉ ra các khoảng đồng biến và nghịch biến của hàm số đã cho.
2. b) Tính đạo hàm f^′(x) và xét dấu f′(x).
3. c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến, nghịch biến của hàm số với dấu của f′(x).

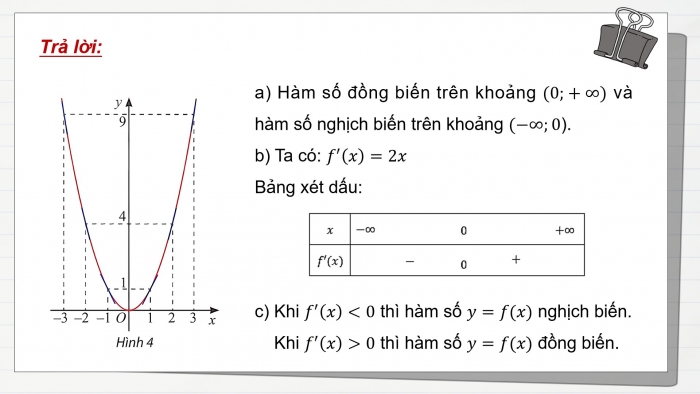
Trả lời: 

1. a) Hàm số đồng biến trên khoảng (0;+∞) và hàm số nghịch biến trên khoảng (−∞;0).
2. b) Ta có: f^′(x)=2x

Bảng xét dấu: 

1. c) Khi f^′(x)<0 thì hàm số y=f(x) nghịch biến.

    Khi f^′(x)>0 thì hàm số y=f(x) đồng biến. 

Kết luận 

Cho hàm số y=f(x) có đạo hàm trên K. 

Nếu f^′(x)>0 với mọi x thuộc K thì hàm số y=f(x) đồng biến trên K. 

Nếu f^′(x)<0 với mọi x thuộc K thì hàm số y=f(x) nghịch biến trên K. 

Ví dụ 2. Chứng minh rằng hàm số g(x)=x/x−1 nghịch biến trên khoảng (1;+∞). 

Giải: 

Hàm số xác định trên (1;+∞)  

Ta có g^′(x)=−1/(x−1)^2<0 với mọi x ϵ (1;+∞) 

Vậy g(x) nghịch biến trên khoảng (1;+∞). 

Chú ý: Khi xét tính đơn điệu của hàm số mà chưa cho khoảng K, ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó. 

Để xét tính đơn điệu của hàm số y=f(x), ta thực hiện các bước sau 

Bước 1: Tìm tập xác định D của hàm số. 

Bước 2: Tính đạo hàm f′(x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f′(x) bằng 0 hoặc đạo hàm không tồn tại. 

Bước 3: Xét dấu f′(x) và lập bảng biến thiên. 

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số. 

Ví dụ 3. Xét tính đơn điệu của các hàm số sau: 

1. a) f(x)=−x^3+3x^2;                             b) g(x)=x+1/x;                              c) ℎ(x)=x^3

Giải: 

2. a) Xét hàm số  f(x)=−x^3+3x^2. Tập xác định: D=R

Ta có f′(x)=−3x^2+6x; f′(x)=0⇔x=0 hoặc x=2 

Bảng biến thiên 

Vậy hàm số f(x)=−x^3+3x^2 đồng biến trên khoảng (0;2), nghịch biến trên các khoảng (− ∞; 0) và (2;+∞). 

1. b) Xét hàm số g(x)=x+1/Tập xác định: D=R\{0}

Ta có g′(x)=1−1/x^2=x^2−1/x^2 

Vì x^2>0 với mọi x ϵ R\{0} nên g′(x) cùng dấu với x^2−1  

Ta có g^′(x)=0⇔x^2−1=0⇔x=−1 hoặc x=1 

Bảng biến thiên 

Vậy hàm số g(x)=x+1/x đồng biến trên khoảng (− ∞;−1) và (1;+∞), nghịch biến 

trên các khoảng (−1; 0) và (0;1). 

1. c) Xét hàm số ℎ(x)=x^3

Tập xác định: D=R 

Ta có ℎ′(x)=3x^2; ℎ′(x)=0⇔x=0 

Bảng biến thiên 

Vậy hàm số ℎ(x)=x^3 đồng biến trên R. 

Chú ý: 

1. a) Nếu hàm số y=f(x) có đạo hàm trên K, f^′(x)≥0 với mọi x∈K và f^′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số     đồng biến trên K.
2. b) Nếu hàm số y=f(x) có đạo hàm trên K, f^′(x)≤0 với mọi x∈K và f^′(x)=0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K.
3. c) Nếu f^′(x)=0 với mọi x∈K thì hàm số không đổi trên K.

Thực hành 2 

Xét tính đơn điệu của hàm số sau: 

1. a) f(x)=x^3−6x^2+9x;               b) g(x)=1/x.

Giải: 

Ta có: f^′(x)=3x^2−12x+9; f^′(x)=0⟺[█(x=1@x=3)┤ 

Bảng biến thiên: 

Hàm số đồng biến trên các khoảng (−∞;1) và (3;+∞). 

Hàm số nghịch biến trên khoảng (1;3). 

1. b) Tập xác định: D=ℝ\{0}.

Ta có: g^′(x)=−1/x^2<0 

Bảng biến thiên: 

Hàm số nghịch biến trên các khoảng (−∞;0) và (0;+∞). 

Thực hành 3 

Chứng minh rằng hàm số f(x)=3x−sinx đồng biến trên ℝ. 

Giải: 

Tập xác định: D=ℝ 

Ta có: f^′(x)=3−cosx 

Vì −1≤cosx≤1 nên f^′(x)>0 

Vậy hàm số đồng biến trên ℝ. 

Vận dụng 1 

Hãy trả lời câu hỏi trong Hoạt động khởi động bằng cách xét dấu đạo hàm của hàm số ℎ(t)=6t^3−81t^2+324t với 0≤t≤8. 

Giải: 

Ta có: ℎ^′(t)=18t^2−162t+324; ℎ^′(t)=0⇔[█(t=3@t=6)┤ 

Bảng biến thiên: 

Trong khoảng thời gian (0;3) và (6;8) khinh khí cầu tăng dần độ cao, trong khoảng thời gian (3;6) khinh khí cầu giảm dần độ cao. 

02 CỰC TRỊ CỦA HÀM SỐ 

Khái niệm cực trị của hàm số 

...