Giáo án Toán đại số 12 chân trời sáng tạo 2024 (file word)
Tải giáo án Toán đại số 12 chân trời sáng tạo 2024 (file word) mới nhất. Giáo án word, font chữ Time New Roman, tải về chỉnh sửa được. Bộ giáo án được soạn chi tiết, cẩn thận chuẩn theo mẫu công văn 5512 mới sẽ giúp giáo viên dễ dàng triển khai các hoạt động giảng dạy. Mời thầy cô tham khảo
Rõ nét về file powerpoint trình chiếu. => Xem thêm
Ngày soạn: .../.../...
Ngày dạy: .../.../...
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
- MỤC TIÊU:
- Kiến thức:
Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
- Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.
- Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
- Vận dụng đạo hàm và tính đơn điệu của hàm số để giải quyết một số vấn đề liên quan đến thực tiễn.
- Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá.
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm.
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng: tư duy và lập luận toán học, giao tiếp toán học; mô hình hóa toán học; giải quyết vấn đề toán học.
- Tư duy và lập luận toán học: Lập luận, phân tích, so sánh để xác định được khái niệm tính đồng biến, nghịch biến của hàm số, từ đó xác định được các điểm cực trị và giá trị cực trị của hàm số.
- Mô hình hóa toán học: Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên dựa vào dấu của đạo hàm.
- Giải quyết vấn đề toán học: sử dụng dấu của đạo hàm để xác định tính đồng biến, nghịch biến, xác định cực trị của hàm số.
- Giao tiếp toán học: Đọc hiểu thông tin toán học từ đồ thị, bảng biến thiên.
- Sử dụng công cụ, phương tiện học toán: sử dụng máy tính cầm tay để tính giá trị cực trị của hàm số.
- Phẩm chất
- Tích cực thực hiện nhiệm vụ khám phá, thực hành, vận dụng.
- Có tinh thần trách nhiệm trong việc thực hiện nhiệm vụ được giao.
- Khách quan, công bằng, đánh giá chính xác bài làm của nhóm mình và nhóm bạn.
- Tự tin trong việc tính toán; giải quyết bài tập chính xác.
- THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1 - GV: SGK, SGV, Tài liệu giảng dạy, giáo án PPT, PBT (ghi đề bài cho các hoạt động trên lớp), các hình ảnh liên quan đến nội dung bài học,...
2 - HS:
- SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
- HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
- a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
- b) Nội dung: HS đọc bài toán mở đầu và thực hiện bài toán dưới sự dẫn dắt của GV (HS chưa cần giải bài toán ngay).
- c) Sản phẩm: HS nhận biết được các thông tin trong bài toán và dự đoán câu trả lời cho câu hỏi mở đầu theo ý kiến cá nhân.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV chiếu Slide dẫn dắt và yêu cầu HS thảo luận và nêu dự đoán về câu hỏi mở đầu (chưa cần HS giải):
Trong 8 phút đầu kể từ khi xuất phát, độ cao (tính bằng mét) của khinh khí cầu vào thời điểm phút được cho bởi công thức . Đồ thị của hàm số được biểu diễn trong hình bên.
Trong khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao?
Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm và thực hiện yêu cầu theo dẫn dắt của GV.
Bước 3: Báo cáo, thảo luận: GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV ghi nhận câu trả lời của HS, trên cơ sở đó dẫn dắt HS vào tìm hiểu bài học mới: “Ở lớp dưới chúng ta đã học về tính đồng biến và nghịch biến của một hàm số. Trong bài học ngày hôm nay, chúng ta sẽ học cách xét tính đơn điệu của hàm số dựa vào dấu của đạo hàm và cách tìm điểm cực trị, giá trị cực trị của hàm số.”
- HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Tính đơn điệu của hàm số
- a) Mục tiêu:
- HS nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
- HS thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.
- b) Nội dung:
- HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện HĐKP1; Thực hành 1, 2, 3, Vận dụng 1 và các Ví dụ.
- c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi, HS nhận biết được tính đồng biến, nghịch biến của hàm số, thể hiện được tính đơn điệu của hàm số trong bảng biến thiên.
- d) Tổ chức thực hiện:
|
HĐ CỦA GV VÀ HS |
SẢN PHẨM DỰ KIẾN |
|
Bước 1: Chuyển giao nhiệm vụ: NV1: Nhắc lại về tính đồng biến, nghịch biến của hàm số - GV yêu cầu học sinh nhắc lại về tính đồng biến, nghịch biến của hàm số. + Hàm số có tính chất như thế nào được gọi là đồng biến, nghịch biến?
+ Hàm số đồng biến có dạng đồ thị như thế nào? Hàm số nghịch biến có dạng đồ thị như thế nào? - GV mời 2 HS đứng tại chỗ trình bày. - GV nhận xét, chốt đáp án và khẳng định “Hàm số đồng biến hoặc nghịch biến trên được gọi chung là đơn điệu trên ”.
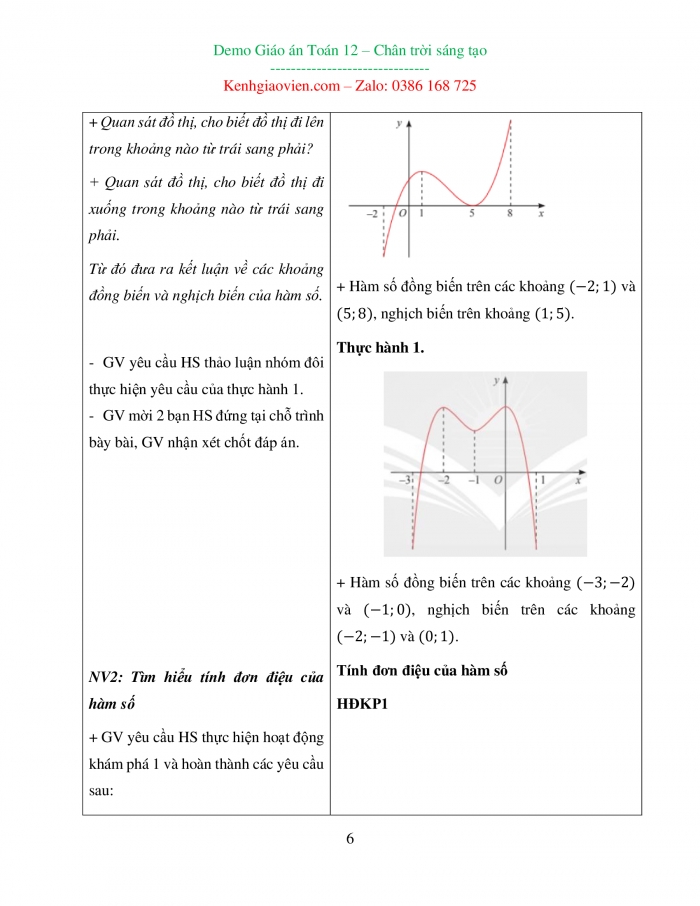
- GV yêu cầu HS tìm hiểu Ví dụ 1 (SGK – tr.7) và hoàn thành yêu cầu. + Quan sát đồ thị, cho biết đồ thị đi lên trong khoảng nào từ trái sang phải? + Quan sát đồ thị, cho biết đồ thị đi xuống trong khoảng nào từ trái sang phải. Từ đó đưa ra kết luận về các khoảng đồng biến và nghịch biến của hàm số.
- GV yêu cầu HS thảo luận nhóm đôi thực hiện yêu cầu của thực hành 1. - GV mời 2 bạn HS đứng tại chỗ trình bày bài, GV nhận xét chốt đáp án.
NV2: Tìm hiểu tính đơn điệu của hàm số + GV yêu cầu HS thực hiện hoạt động khám phá 1 và hoàn thành các yêu cầu sau: Cho hàm số .
a) Từ đồ thị của hàm số , hãy chỉ ra các khoảng đồng biến và nghịch biến của hàm số đã cho. b) Tính đạo hàm và xét dấu .
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến, nghịch biến của hàm số với dấu của . - GV mời 3 HS lên bảng trình bày. - GV nhận xét, kết luận về tính đơn điệu của hàm số.
- GV yêu cầu HS tìm hiểu ví dụ 2 (SGK – Tr.8) - GV mời 1 HS đứng tại chỗ trình bày lại. - GV đặt câu hỏi: Ta xét tính đơn điệu của hàm số trên tập hợp nào? Từ đó đưa chú ý cho HS. - GV yêu cầu HS đưa ra các bước thực hiện xét tính đơn điệu của một hàm số.
- GV yêu cầu HS thảo luận nhóm đôi tìm hiểu Ví dụ 3. - GV mời 3 bạn HS lên bảng trình bày bài. - GV nêu chú ý cho HS.
- GV chia lớp thành 4 nhóm để thảo luận và thực hiện phần Thực hành 2. + Nhóm 1 và 2, thực hiện câu a). + Nhóm 3 và 4, thực hiên câu b). + Các nhóm thực hiện trao đổi, thống nhất đáp án trong 6 - 8 phút. - Xét tính đơn điệu của các hàm số sau: a) ; b) . + Sau thời gian thảo luận, GV mời đại diện từng nhóm lên thực hiện bài giải của nhóm mình. + HS dưới lớp quan sát, thực hiện bài làm vào vở cá nhân. + GV quan sát, nhận xét bài làm của HS và rút ra kinh nghiệm làm bài cho HS.
- GV yêu cầu HS thực hiện nhóm đôi hoàn thành yêu cầu của thực hành 3: Chứng minh rằng hàm số đồng biến trên . + Tính của hàm số trên tập xác định. + Giá trị của nằm trong khoảng nào? Từ đó xét dấu của . - GV mời 1 HS lên bảng trình bày bài, các bạn theo dõi nhận xét bài. - GV chốt đáp án. - GV đặt câu hỏi: Hãy trả lời câu hỏi trong Hoạt động khởi động bằng cách xét dấu đạo hàm của hàm số với . Bước 2: Thực hiện nhiệm vụ: - HĐ cá nhân: HS suy nghĩ, hoàn thành vở. Cả lớp chú ý thực hiện các yêu cầu của GV, chú ý bài làm các bạn và nhận xét. - GV: quan sát và trợ giúp HS. Bước 3: Báo cáo, thảo luận: - HS trả lời trình bày miệng/ trình bày bảng, cả lớp nhận xét, GV đánh giá, dẫn dắt, chốt lại kiến thức. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm + Nhắc lại về tính đồng biến, nghịch biến của hàm số. + Tính đơn điệu của hàm số. |
1. Tính đơn điệu của hàm số Nhắc lại về tính đồng biến, nghịch biến của hàm số Kí hiệu là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số xác định trên . Hàm số gọi là đồng biến (tăng) trên nếu với mọi thuộc mà thì . Hàm số gọi là nghịch biến (giảm) trên nếu với mọi thuộc mà thì . Nếu hàm số đồng biến trên thì đồ thị của nó đi lên từ trái sang phải.
Nếu hàm số nghịch biến trên thì đồ thị của nó đi xuống từ trái sang phải.
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số có đồ thị cho ở Hình 2.
+ Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng . Thực hành 1.
+ Hàm số đồng biến trên các khoảng và , nghịch biến trên các khoảng và . Tính đơn điệu của hàm số HĐKP1
a) Hàm số đồng biến trên khoảng và hàm số nghịch biến trên khoảng ). b) Ta có: Bảng xét dấu:
c) Khi thì hàm số nghịch biến. Khi thì hàm số đồng biến.
Kết luận Cho hàm số có đạo hàm trên . Nếu với mọi thuộc thì hàm số đồng biến trên . Nếu với mọi thuộc thì hàm số nghịch biến trên . Ví dụ 2 (SGK – tr.8) Hướng dẫn giải – SGK – tr.8
Chú ý: Khi xét tinh đơn điệu của hàm số mà chưa cho khoảng , ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó. Các bước thực hiện Để xét tính đơn điệu của hàm số , ta thực hiện các bước sau: Bước 1: Tìm tập xác định của hàm số. Bước 2: Tính đạo hàm của hàm số. Tìm các điểm thuộc mà tại đó đạo hàm bằng 0 hoặc đạo hàm không tồn tại. Bước 3: Xét dấu và lập bảng biến thiên. Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số. Ví dụ 3 (SGK – Tr.8) Hướng dẫn giải – SGK – tr.8-9. Chú ý: a) Nếu hàm số có đạo hàm trên , với mọi và chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên . b) Nếu hàm số có đạo hàm trên , với mọi và chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên . c) Nếu với mọi thì hàm số không đổi trên . Thực hành 2. a) Tập xác định: Ta có:
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và Hàm số nghịch biến trên khoảng . b) Tập xác định: . Ta có: Bảng biến thiên:
Hàm số nghịch biến trên các khoảng và . Thực hành 3. Tập xác định: . Ta có: Vì nên Vậy hàm số đồng biến trên .
Vận dụng 1. Ta có:
Bảng biến thiên:
Trong khoảng thời gian và khinh khí cầu tăng dần độ cao, trong khoảng thời gian khinh khí cầu giảm dần độ cao.
|
Hoạt động 2: Cực trị của hàm số
- a) Mục tiêu:
- Nhận biết được điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
- b) Nội dung:
- HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện HĐKP2, 3; Thực hành 4, 5; Vận dụng 2 và các Ví dụ.
- c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi, HS nhận biết được cực trị và tính được giá trị cực trị của hàm số.
- d) Tổ chức thực hiện:
|
HĐ CỦA GV VÀ HS |
SẢN PHẨM DỰ KIẾN |
|
Bước 1: Chuyển giao nhiệm vụ: NV1: Tìm hiểu khái niệm cực trị của hàm số - GV cho HS thực hiện thảo luận nhóm đôi thực hiện HĐKP2 Quan sát đồ thị của hàm số
a) Tìm khoảng chứa điểm mà trên đó với mọi . b) Tìm khoảng chứa điểm mà trên đó với mọi . c) Tồn tại hay không khoảng chứa điểm mà trên đó với mọi hoặc với mọi ? - GV chỉ định 3 HS lên bảng trình bày bài giải. - HS dưới lớp nhận xét. - GV giới thiệu khái niệm về các điểm cực trị và giá trị cực trị của hàm số
- GV đặt câu hỏi gợi mở đưa chú ý: + Các điểm cực tiểu và cực đại được gọi chung là gì? Giá trị cực đại và cực tiểu được gọi là gì? + Một hàm số có thể có mấy cực trị? + Nếu là điểm cực trị của hàm số thì điểm là một điểm cực trị của đồ thị hàm số có tọa độ là gì?
- GV cho HS thảo luận nhóm tìm hiểu Ví dụ 4. + Tìm cực trị của hàm số có đồ thị được cho ở Hình 7.
- GV cho HS làm bài cá nhân hoàn thành yêu cầu Thực hành 4. + Tìm các điểm cực trị của hàm số có đồ thị cho ở Hình 8.
NV2: Tìm hiểu cách tìm cực trị của hàm số - GV cho HS thực hiện thảo luận nhóm đôi thực hiện HĐKP3. Đồ thị của hàm số
Được cho ở Hình 9.
a) Tìm điểm cực đại và điểm cực tiểu của hàm số. b) Tại hàm số có đạo hàm không? c) Thay mỗi dấu ? bằng kí hiệu thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của khi đi qua điểm cực đại và điểm cực tiểu.
+ Trong các khoảng hàm số đồng biến hay nghịch biến? Từ đó suy ra dấu của . - GV tổng kết về cách tìm điểm cực trị thông qua dấu của đạo hàm.
- GV yêu cầu HS tìm hiểu Ví dụ 5: Tìm cực trị của hàm số . + Tìm tập xác định của hàm số đã cho. + Tính . + Vẽ bảng biến thiên và tìm cực trị của hàm số. - GV mời 1 HS lên bảng trình bày bài. - Từ đó, GV yêu cầu HS khái quát các bước tìm cực trị của một hàm số.
- HS áp dụng quy tắc thực hiện ví dụ 6: Tìm cực trị của hàm số . - GV đặt câu hỏi mở rộng: Nếu và không đổi dấu khi qua điểm thì hàm số có cực trị không? Từ đó đưa ra chú ý cho HS.
- GV yêu cầu HS hoàn thành Thực hành 5. Tìm cực trị của hàm số
- GV mời 1 HS lên bảng trình bày. - HS ở dưới nhận xét, GV chốt đáp án.
- GV yêu cầu HS thảo luận nhóm, hoàn thành yêu cầu phần Vận dụng 2. Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số với . Tìm tọa độ các đỉnh của lát cắt dãy núi trên đoạn . + Các tọa độ đỉnh của lát cắt dãy núi có phải cực trị của hàm số trên đoạn không? + Áp dụng quy tắc tìm cực trị để tìm các tọa độ đỉnh đó. Bước 2: Thực hiện nhiệm vụ: - HĐ cá nhân: HS suy nghĩ, hoàn thành vở. - HĐ cặp đôi: các thành viên trao đổi, đóng góp ý kiến và thống nhất đáp án. Cả lớp chú ý thực hiện các yêu cầu của GV, chú ý bài làm các bạn và nhận xét. - GV: quan sát và trợ giúp HS. Bước 3: Báo cáo, thảo luận: - HS trả lời trình bày miệng/ trình bày bảng, cả lớp nhận xét, GV đánh giá, dẫn dắt, chốt lại kiến thức. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm + Cách tìm cực trị và giá trị cực trị của hàm số. |
2. Cực trị của hàm số Khái niệm cực trị của hàm số HĐKP2
a) Trong khoảng thì với mọi . b) Trong khoảng thì với mọi . c) Không tồn tại khoảng chứa điểm mà trên đó với mọi hoặc với mọi
Khái niệm Cho hàm số xác định trên tập hợp và . · Nếu tồn tại một khoảng chứa điểm và sao cho với mọi thì được gọi là một điểm cực đại, được gọi là giá trị cực đại của hàm số , kí hiệu . · Nếu tồn tại một khoảng chứa điểm và sao cho với mọi thì được gọi là một điểm cực tiểu, được gọi là giá trị cực tiểu của hàm số , kí hiệu .
Chú ý: a) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (còn gọi là cực trị) của hàm số. b) Nếu là một cực trị (điểm cực trị, điểm cực tiểu) của hàm số thì ta cũng nói hàm số đạt cực trị (cực đại, cực tiểu) tại . c) Hàm số có thể đạt cực đại và cực tiểu tại nhiều điểm trên . d) Nếu là điểm cực trị của hàm số thì điểm là một điểm cực trị của đồ thị hàm số . Ví dụ 4 (SGK – tr.10)
Hướng dẫn giải (SGK – tr.10) Thực hành 4. Hàm số có: + là điểm cực tiểu vì với mọi . + là điểm cực đại vì với mọi . + là điểm cực tiểu vì với mọi .
Tìm cực trị của hàm số HĐKP3
a) là điểm cực đại của hàm số và là điểm cực tiểu của hàm số. b) Tại hàm số không có đạo hàm. c) Bảng biến thiên:
Từ bảng biến thiên, ta thấy đổi dấu khi đi qua điểm cực đại và điểm cực tiểu.
- Cho hàm số liên tục trên khoảng chứa điểm và có đạo hàm trên các khoảng và . Khi đó: - Nếu với mọi và với mọi thì hàm số đạt cực tiểu tại điểm - Nếu với mọi và với mọi thì hàm số đạt cực đại tại điểm Ví dụ 5 (SGK – tr.11) Hướng dẫn giải (SGK – tr.11)
Nhận xét: Để tìm cực trị của hàm số ta thực hiện các bước sau: Bước 1: Tìm tập xác định của hàm số. Bước 2: Tính đạo hàm của hàm số. Tìm các điểm thuộc mà tại đó đạo hàm bằng 0 hoặc đạo hàm không tồn tại. Bước 3: Lập bảng biến thiên của hàm số. Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số. Ví dụ 6 (SGK – Tr.12) Hướng dẫn giải (SGK – tr.12).
Chú ý: a) Nếu và không đổi dấu khi qua điểm thì hàm số không có cực trị tại . b) Nếu không đổi dấu trên khoảng thì không có cực trị trên khoảng đó. Thực hành 5. Tập xác định: . Ta có:
Bảng biến thiên:
Hàm số đại cực đại tại và đạt cực tiểu tại . Vận dụng 2.
Ta có:
Khi đó:
Bảng biến thiên
Vậy tọa độ đỉnh của lát cắt dãy núi trên đoạn [0 là: và . |
- HOẠT ĐỘNG LUYỆN TẬP
- a) Mục tiêu:Học sinh củng cố lại kiến thức đã họcthông qua một số bài tập.
- b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1; 2; 3; 4(SGK – tr.13), HS trả lời các câu hỏi trắc nghiệm.
- c) Sản phẩm học tập: Câu trả lờicủa HS về vận dụng khái niệm, công thức xét tính đơn điệu của hàm số và tìm cực trị, giá trị cực trị của hàm số.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV cho HS làm câu hỏi trắc nghiệm:
Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên ?
|
A. . |
C. |
|
B. . |
D. . |
Câu 2. Hàm số nghịch biến trên khoảng nào sau đây?
|
A. . |
B. . |
C. . |
D. . |
Câu 3. Cho hàm số có bảng biến thiên như sau:
Chọn khẳng định đúng:
- Hàm số đồng biến trên khoảng .
- Hàm số đặt cực đại tại điểm .
- Giá trị cực đại của hàm số là .
- Hàm số nghịch biến trên khoảng .
Câu 4. Cho hàm số có bao nhiêu điểm cực trị?
|
A. 2. |
B. |
C. . |
D. . |
Câu 5. Cho hàm số . Mệnh đề nào sau đây là đúng?
- Hàm số đặt cực đại tại , đạt cực tiểu tại .
- Hàm số đặt cực tiểu tại , đạt cực đại tại .
- Hàm số đặt cực tiểu tại và , đạt cực đại tại .
- Hàm số đặt cực đại tại và , đạt cực tiểu tại .
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận: - Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Kết quả:
Bài 1.
a)
Hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên các khoảng và .
- b)
Hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên khoảng .
Bài 2.
- a)
Tập xác định: .
Ta có: .
Khi đó:
Bảng biến thiên :
Hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên khoảng .
Hàm số đạt cực đại tại điểm và đạt cực tiểu tại điểm .
- b)
Tập xác định : .
Ta có:
Khi đó :
Bảng biến thiên :
Hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên các khoảng và .
Hàm số đạt cực đại tại điểm và đạt điểm cực tiểu tại điểm .
Bài 3.
- a) .
Tập xác định : .
Ta có: .
Khi đó:
Bảng biến thiên :
Hàm số đạt cực đại tại và đạt cực tiểu tại điểm .
- b)
Tập xác định : .
Ta có: .
Vậy hàm số không có cực trị.
- c)
Tập xác định: .
Ta có :
Bảng biến thiên :
Hàm số đạt cực đại tại điểm .
Bài 4.
Tập xác định : .
Ta có : .
Vậy hàm số đã cho nghịch biến trên từng khoảng xác định.
|
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
|
B |
D |
C |
B |
A |
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác.
- GV chú ý cho HS các lỗi sai hay mắc phải khi thực hiện giải bài tập.
- HOẠT ĐỘNG VẬN DỤNG
- a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng thực tế để nắm vững kiến thức.
- HS thấy sự gần gũi toán học trong cuộc sống, vận dụng kiến thức vào thực tế, rèn luyện tư duy toán học qua việc giải quyết vấn đề toán học
- b) Nội dung: HS sử dụng SGK và vận dụng kiến thức để trao đổi và thảo luận hoàn thành các bài toán theo yêu cầu của GV.
- c) Sản phẩm: HS hoàn thành các bài tập được giao.
- d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS hoạt động hoàn thành bài tập 5; 6; 7 (SGK – tr.13).
Bước 2: Thực hiện nhiệm vụ:
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận: GV mời đại diện một vài HS trình bày miệng.
Kết quả:
Bài 5.
- a) Ta có :
- b)
Mặt khác: và
Vậy
Vậy kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Bài 6.
- a) Ta có :
.
.
- b) Ta có :
Bảng biến thiên :
Kết luận : Vận tốc của chất điểm tăng trong khoảng và vận tốc của chất điểm giảm trong khoảng .
Bài 7.
Từ hình vẽ, ta có : Hàm số đồng biến trên khoảng và .
Hàm số nghịch biến trên khoảng và .
Ta có bảng xét dấu như sau :
Hàm số đạt cực đại tại điểm và đạt cực tiểu tại điểm và .
Bước 4: Kết luận, nhận định:
- GV nhận xét, đánh giá khả năng vận dụng làm bài tập, chuẩn kiến thức và lưu ý thái độ tích cực khi tham gia hoạt động và lưu ý lại một lần nữa các lỗi sai hay mắc phải cho lớp.
* HƯỚNG DẪN VỀ NHÀ
- Ghi nhớ kiến thức trong bài.
- Hoàn thành bài tập trong SBT.
- Chuẩn bị bài sau “Giá trị lớn nhất, giá trị nhỏ nhất của hàm số”.
Hình ảnh về file sile, ppt trình chiếu
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
.....
=> Còn nữa.... Files tải về, sẽ có đầy đủ nội dung bài học
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
Từ khóa tìm kiếm:
Giáo án Toán đại số 12 chân trời sáng tạo, Soạn giáo án mới nhất Toán đại số 12 chân trời sáng tạo. tải giáo án sách mới lớp 12 năm học 2023-2024
